基于三次指数平滑法的集装箱吞吐量预测

程雪平 林国龙

上海海事大学信息工程学院计算机系 上海 200135

0 引言

港口集装箱吞吐量的预测对于港口未来的发展有着极为重要的影响。港口集装箱吞吐量的预测对于合理科学的港口布局，基本设施投资规模，营运策略，发展战略以及与输运相关的综合运输的规划是十分重要的。

目前对于港口吞吐量的预测方法主要有定量与定性两种方法。定量方法主要有：灰色模型预测法，回归分析法，弹性系数法、指数平滑法等；定性分析方法主要有：专家分析法，情景分析法等。灰色模型预测法对样本条件要求较低，但是随着基数的增大，数据增速加快，预测效果随着年份的增加效果逐渐变差，对于长期的集装箱吞吐量的预测不能有很好的效果，不适合宁波港集装箱吞吐量的预测；回归分析法在港口集装箱吞吐量预测中应用的比较普遍，它是通过研究预测对象与相关因素的相互关系来预测的，因此在利用回归预测模型进行推测时需要快速更新资料并且需要根据专业知识做出定性判断后才可以进行预测；弹性系数法通过建立港口集装箱吞吐量与港口所在地国民经济指标的弹性模型计算港口集装箱吞吐量对国民经济指标的弹性系数，再根据国民经济发展规划指标利用弹性系数预测港口集装箱吞吐量。弹性系数法用于短期预测效果是显著的。但是，由于经济的发展受很多复杂因素的影响，弹性系数自身也会有变化，其预测的结果不是很理想。指数平滑法是根据历史资料上期实际数和预测值，用指数加权法进行预测的一种方法，其优点是只要有上期实际数和上期预测值，就可以计算下期的预测值。这样可以节省很多数据和处理数据的时间，减少数据的存储量，是一种实用的预测方法，本文将使用指数平滑预测技术对宁波港的集装箱吞吐量进行预测。

1 三次指数平滑预测法

指数平滑法是一种时间序列分析预测方法。时间序列分析预测方法模型的建立根据其适用性的不同可以分为全期平均法、移动平均法、一次指数平滑法、二次指数平滑法及三次指数平滑法等。简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用；移动平均法则不考虑较远期的数据，并在加权移动平均法中给予近期资料更大的权重；而指数平滑法则兼容了全期平均和移动平均所长，不舍弃过去的数据，但是仅给予逐渐减弱的影响程度，即随着数据的远离，赋予逐渐收敛为零的权数。当数据单纯围绕某一水平作随机跳动时，应采用一次平滑预测模型；当数据具有持续的线性增长或下降趋势时，应采用二次平滑预测模型；当数据具有持续的曲线增长或下降趋势时，应采用三次平滑预测模型。通过对宁波港近几年集装箱吞吐量的曲线图的观察，采取三次指数平滑模型是合适的选择。指数平滑法将反映历史变化情况的统计数据，加以大致修匀平滑，以便分析变量的演变趋势。指数平滑法作为一种典型的时间序列预测方法，它认为数据的重要程度按时间上的近远呈非线性递减。即近期数据影响价值大，权数亦大；远期数据影响价值小，权数亦小。

2 三次指数平滑预测模型的建立

设n个原始数据组成一时间序列为： y1,y2,y3,...,yt，三次指数平滑模型为：

其中：

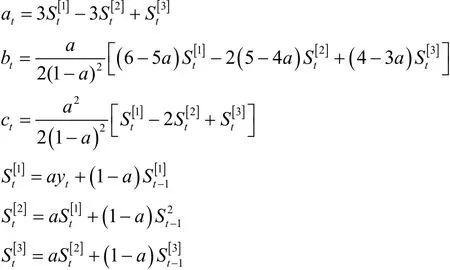
3 宁波港集装箱吞吐量预测

表1 宁波港集装箱历年吞吐量/(万标箱)

根据表1中的数据可做出宁波港2000年～2005年集装箱吞吐量如下散点图：

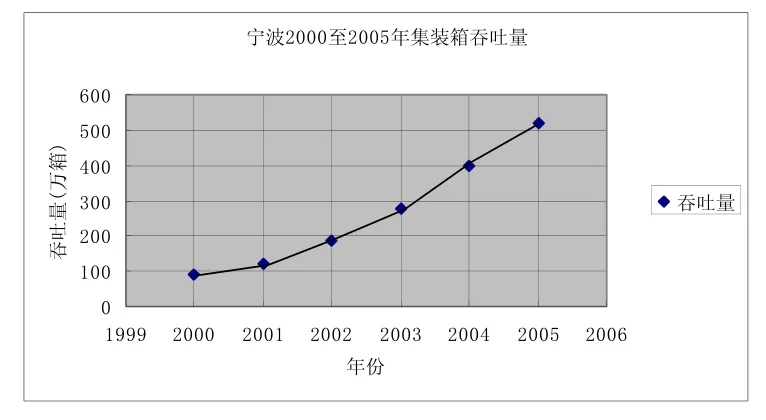
可以看出宁波港在此时间序列数据具有迅速明显的变动趋向，因此a的值可以选择的范围为 0.6～0.8之间，在本文中为了使预测值更加的准确，采用均方误差最小的方法来确定a值：把该组数据分为两段，前5个数据(即2000～2004)为一组，后三个数据(即2005～2007)为一组，利用VC编制计算机程序，以前5个数据为依据建立预测模型，来对后3个数据进行事后预测，以事后预测模型的预测结果的 MSE(均方误差)最小作为评价准则，从而选取最合理的a值，考虑到三次指数平滑法为时间序列预测法，在计算 MSE时，对其去当年的数据的方法。

式中，n为预测数据的数；Y(t)表示预测值；X(t)表示实际值。

根据 S1= a * y1+ ( 1 − a ) *S0，当欲用指数平滑法时才开始收集数据，则不存在 y0。无从产生 S0，自然无法根据指数平滑法的公式求出 S1，指数平滑法定义 S1为初始值。初始值的确定也是指数平滑法过程的一个重要条件。如果能够找到y1以前的历史资料，那么，初始值 S1的确定是不成问题的。数据较少时可用全期平均、移动平均法；数据较多时，可用最小二乘法。但不能使用指数平滑法本身确定初始值，因为数据必会枯竭。

如果仅有从 y1开始的数据，那么确定初始值的方法有：

（1）取 S1等于 y1；

（2）待积累若干数据后，取 S1等于前面若干数据的简单算术平均数，如： S1= ( y1+ y2+ y3)/3等。

本文将采用这几种方法相结合的方式来确定其相对应的初始值。对2005年进行预测时，因为用2004年来预测2005年的值，可把2003年的实际值作为其初始值，即从2004年按T=1，St−1=277.2；从2003年按其平均值来计算，此时 St−1=（121.3+185.9+277.2）/3=194.8按T=2，从2002年也按全期平均值来计算 St−1=132.4667，T=3；这样就得到2005年集装箱吞吐量的三个预测值，然后取平均数得到最终的预测值。

a值可分别取a=0.6，0.7，0.8利用前 5个数预测后三个数，再利用公式得出均方误差最小的MSE值。

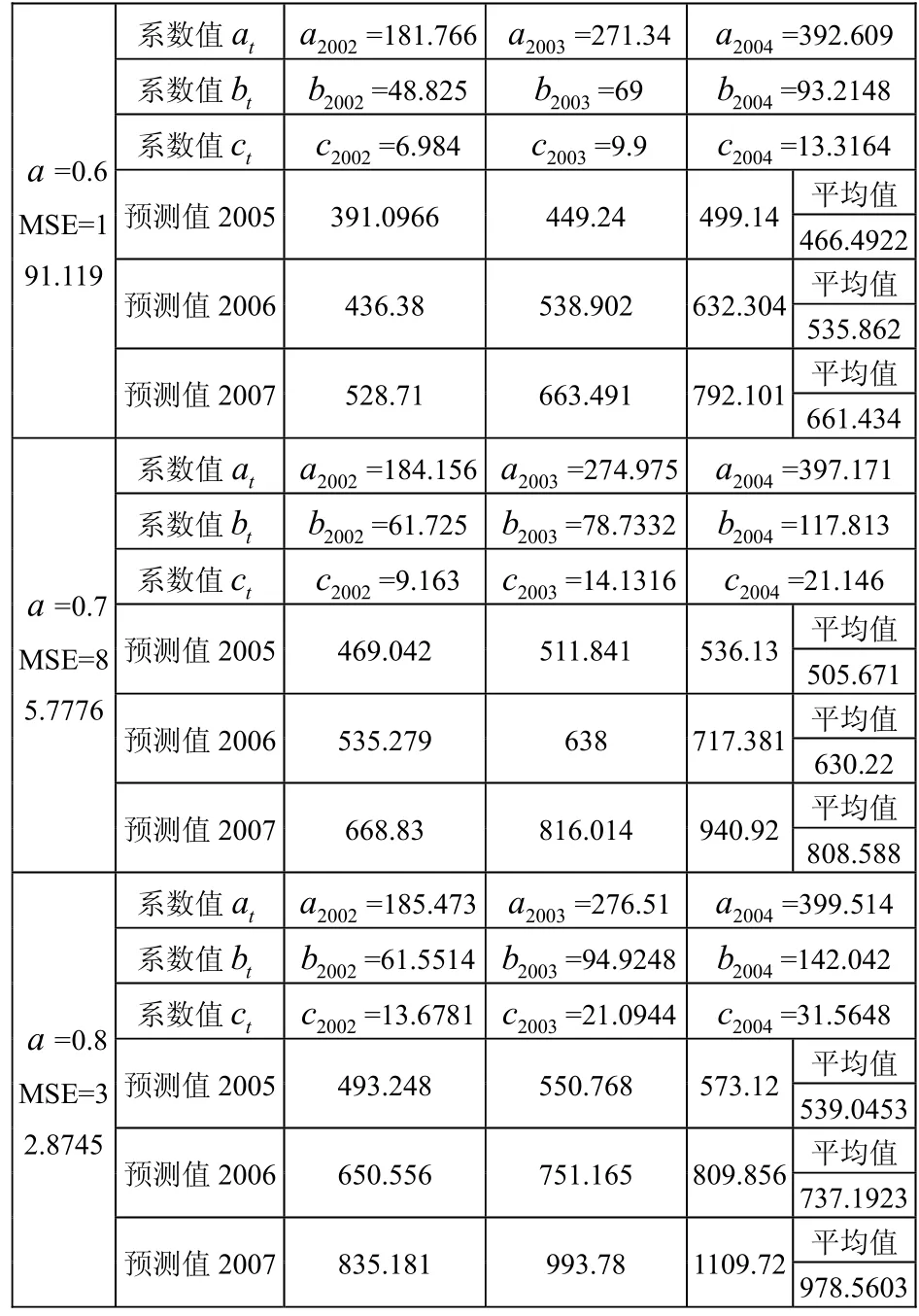
表2 取不同a值所得到的预测值以及最小均方差值

从表2可以看出当a取0.8时其对应的均方误差值最小为32.8745。

根据此a的取值我们可以对宁波港未来几年的集装箱吞吐量进行预测，预测结果如表3。

表3 2008年～2010年宁波港集装箱吞吐量预测(万标箱)

4 结束语

近年来宁波港国际集装箱吞吐量保持高速增长，增幅居全国前列，近来虽然受全球金融危机的影响，增幅有所下降，但是相信未来宁波港集装箱吞吐量仍然会保持良好的增长势头，本文在前几年预测相对准确的情况下采用三次指数平滑法对未来几年宁波港国际集装箱吞吐量进行了预测，具有可信性。

[1]韩增林.集装箱港口发展与布局研究[M].北京:海洋出版社.2006.

[2]黄荣富.三次指数平滑法在港口吞吐量预测中的应用[J].港口管理.2003.

[3]黄顺泉.关于港口吞吐量预测方法选择的探讨[J].集装箱化.2003.