混油对成品油管网优化设计的影响分析

付晓东, 王 岳, 付吉强, 王爱萍

(1.辽宁石油化工大学石油天然气工程学院,辽宁抚顺 113001; 2.大连理工大学化工学院,辽宁大连 116023)

混油对成品油管网优化设计的影响分析

付晓东1, 王 岳1, 付吉强1, 王爱萍2

(1.辽宁石油化工大学石油天然气工程学院,辽宁抚顺 113001; 2.大连理工大学化工学院,辽宁大连 116023)

考虑成品油顺序输送中产生混油的特点,以管道生命周期内收益最高为目标,管径、壁厚为决策变量,建立了成品油管网优化设计的数学模型。分别利用扩散理论推导的变径管混油量计算公式和经验公式计算混油量,并采用遗传算法求解该模型。计算表明,混油损失费用占整个设计的3%～10%,并且与年输送批次数、每一批次输送的油品种类数、单位体积的混油处理费用等因素相关,一般情况下不能忽略不计,可以采用权重系数法生成多种设计方案以供选择。而不同的混油计算公式结果往往不同,在实际工程中应选择与本工程最接近的公式进行计算。

混油; 成品油; 管网; 优化设计; MA TLAB; 遗传算法

成品油管网优化设计是在满足各种设计约束条件下,寻求最优的管材、管径、管壁厚度、操作压力、泵站数目、油品输送顺序、顺序输送周期及批量、混油处理方案等因素的最优组合,使所设计的管道在规定的计算期内获得最佳经济效益[1]。若不考虑泵站数量的影响,以管径和壁厚为决策变量建立优化模型时,主要考虑的是初始投资、管道维护费用以及能耗费用三者之间的平衡,而顺序输送过程中产生的混油损失对优化设计的影响往往被人忽略。初飞雪等[2]采用了赋权有向图来表示成品油管道工艺方案优化设计问题,通过循环调用Dijkstra算法,求解出了前N条最短路径作为最优和次优方案,但没有考虑混油损失对优化设计的影响。黄淑女等[3]利用动态规划求解了成品油工艺方案优化设计模型,没有考虑混油损失,虽然也可以得到最优解,但过程复杂、计算量大,若需要得到多种设计方案时则显得效率不高。遗传算法近年来在天然气管网、给水管网等管网设计中的应用表明,该算法效率高,不依赖于目标函数,具有很强的适应性,适于应用到管网设计中[4]。

对于成品油管网来说,各管段的管径与流速都不相同,影响混油的因素又比较多,目前还没有公认的与实际完全相符的混油计算公式[5]。本文分别利用了不同的混油公式,并采用遗传算法求解,通过比较计算为工程实践提供理论依据。

1 数学模型的建立

按等温输油进行计算,采用现值法,以各管段的管径为决策变量,总投资、管道维护费用现值、能耗费用现值以及混油损失现值之和为目标函数,建立数学模型[6]。

式中,ND-管段数;

Cpj-第j个管段线路初始投资,元;

Cpmj-第j个管段线路运行维护费用现值,元;

Cso-泵站年操作费用现值,元;

Co-混油贬值费用,元。

约束条件的处理采用罚函数法。

1.1 流态约束条件

为了避免增大混油量,雷诺数要大于临界雷诺数

式中,Dj-第j个管段外径,m;

δj-管道计算壁厚,m;

νm-第m种油品的运动粘度,m2/s;

Qj-第j个管段的流量,m3/s。

1.2 压力约束条件

设计压力约束:pmin≤p≤pmax;

进站压力约束:pminin≤pin≤pmaxin。

1.3 钢管规格约束条件

管径约束Dj∈{Dj},壁厚约束δj∈{δj}Dj。

2 混油量的计算

对于成品油管道,在一定时期内,需要根据市场的变化顺序输送多种油品,无法避免的会产生混油,产生贬值费用。

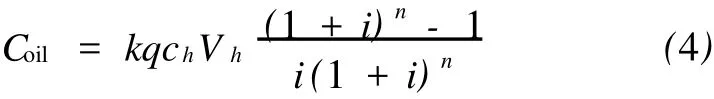
式中,k-每年进行顺序输送的批次数;

q-每一批次中混油段的数量,q=2(m-1),m为每一批次输送的油品种类;

ch-混油处理费用,元/m3;

Vh-每个混油段中产生的混油量,m3;

n-寿命期,取10～15年;

i-折现率,取8%～15%。

对于成品油管网,各管段的直径不同,流速也不同,混油量的计算方法也不同于等管径等流速条件下的计算,一般采用由扩散理论推导的公式或经验公式进行计算[7-9]。

2.1 由扩散理论推导的变径管混油量计算公式

在混油扩散理论中,引入了湍流扩散系数DT,它综合了油品交替过程中各种因素对扩散速度的影响,计算DT的可以采用雅勃隆斯基-希兹基洛夫公式。

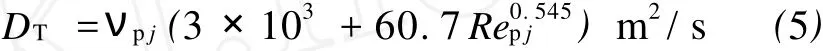
式中,νpj-两种相互交替油品运动粘度的算术平均值,m/s;

Repj-按νpj计算的雷诺数。

设某成品油管网由n+1段不同管径的管段组成,则各管段湍流扩散系数在其时间段的积分之和An为

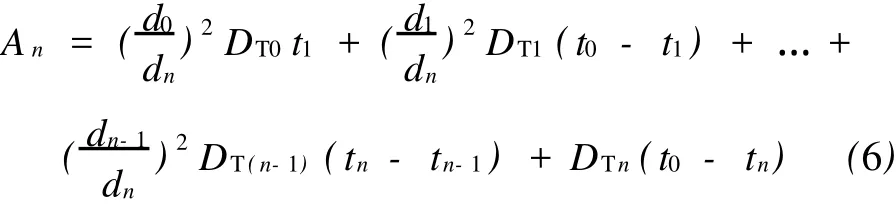
式中,di-第i+1个管段的内径,m;

DTi-第i+1个管段的湍流扩散系数,m2/s;

ti-ti-1-混油的起始接触界面流过各管段的时间,s。

管道终点处,若为对称浓度范围的混油段,则混油体积为

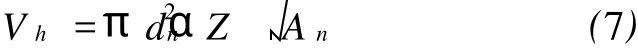
式中,α-修正系数;

Z-与油品浓度有关的变量,对在99%～1%内的混油量,取Z=1.645。

2.2 混油量的经验计算公式

根据《输油管道工程设计规范》中推荐的Austin-Palf rey经验公式,利用当量管径法计算变径管的混油量过程如下:

(1)混油的运动粘度采用以下经验公式计算:

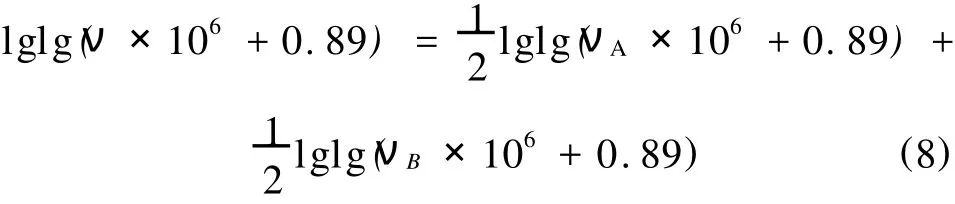
式中,νA-A油在输送温度下的运动粘度,m2/s; νB-B油在输送温度下的运动粘度,m2/s;

ν-混油的计算运动粘度,m2/s。

(2)利用Austin-Palfrey经验公式计算油品在第1个管段中流动所产生的混油长度C1。

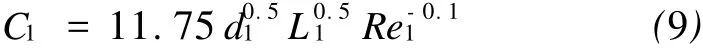
式中,C1-第1个管段的混油长度,m;

d1-第1个管段的管径,m;

L1-第1个管段的长度,m;

Re1-第1个管段的雷诺数。

(3)如果油品在第2个管段的条件下流动,当产生相同混油量时的管段长度即为当量长度L1′。

(4)求在L1′+L2条件下的混油长度C2。

(5)求L1′+L2的当量长度L2′,继续(4)步骤,直到求得最终混油长度Cn。

3 数学模型的求解

由于成品油管网优化设计的数学模型是非线性、多变量的复杂问题,采用常规的优化方法很难高效的求出最优解。而近年来蓬勃发展的智能算法在解决该类管网优化问题中有很大优势,所以本文利用遗传算法进行求解。

遗传算法是通过模拟自然选择和遗传中发生的复制、交叉和变异等现象,从任一初始种群出发,通过随机选择、交叉和变异等操作,产生一群更适应环境的个体,使群体一步一步进化到最适应环境的个体,求得问题的最优解[10]。其主要流程如下:

(1)编码。将解空间的解数据表示成遗传空间的基因型串结构数据。由于本数学模型的决策变量管径为离散变量,决定采用整数编码的方式。

(2)初始群体的形成。随机产生N个初始串结构数据。

(3)适应度值评价检测。适应度函数表明个体的优劣性,将目标函数用罚函数法改进后作为适应度函数。

(4)选择、交叉、变异。通过这一系列操作生成新的群体。

(5)对新群体进行终止条件判断。如符合所要求的终止条件,则得出最优解,否则转到步骤(3)。

4 算例与结果分析

图1为具有多油源(1、2、8号点为油源)的某管网示意图,在稳态下输送成品油。已知管道价格5 500元/t,管道涂层费用100元/m2,施工费用250元/m,电费0.5元/(kW·h)。各管段的输油量、长度见表1,可供选择的管径规格见表2。试确定在以下条件下使总收益最大的管径最优组合:

(1)不计混油损失;

(2)每一批次有两种油品进行顺序输送;

(3)每一批次有四种油品进行顺序输送。

Fig.1 A product pipeline network diagram图1 某成品油管网示意图

表1 各管段参数Table 1 Parameters of each pipeline section

表2可选管径Table 2 Optional diameter

利用MA TLAB遗传算法工具箱进行求解,结果如表3所示。

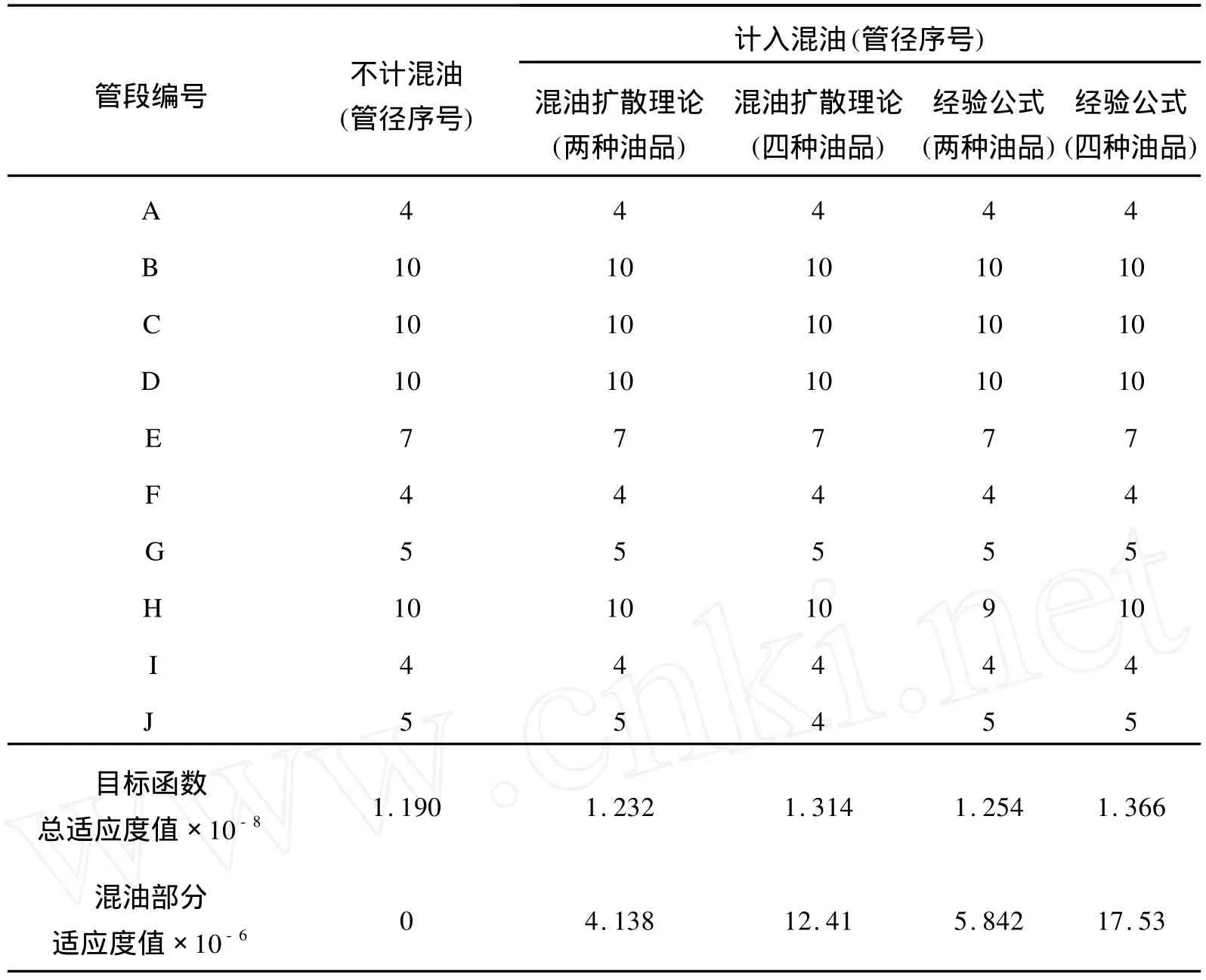
表3 在不同混油条件下计算得到的管径最优组合Table 3 The optimal combination of the diameters in differentm ixed oil conditions

根据以上计算结果分析可知:

(1)成品油管网优化设计模型属于非线性、多变量的复杂数学模型,利用遗传算法可以比较高效、准确的求出令人满意的最优解。而MA TLAB自带的遗传算法工具箱界面友好,操作简便容易上手,可以用于工程实践。

(2)由混油造成的费用占整个设计费用的3%～10%。顺序输送的每一批次的油品种类越少,对整个设计计算的影响越小,有可能没有影响。这种情况下,可以在优化设计中忽略混油的影响。

(3)当输送的油品种类较多,造成的混油段数量也随之增加,此时将会对设计产生影响,影响的程度与年输送批次数、每一批次输送的油品种类数、单位体积的混油处理费用等因素有关,一般情况下不能忽略不计。实际设计中可以采用权重系数法生成多种设计方案以供选择。

(4)本例中,由混油扩散理论和经验公式计算的结果不完全相同,在实际工程中应选择与本工程最接近的公式进行计算。

[1] 初飞雪,吴长春.成品油管道工艺方案优化设计研究[J].石油学报,2006,27(2):116-120.

[2] 初飞雪,吴先策,张宗伟.基于N条最短路径的成品油管道优化设计[J].石油化工高等学校学报,2008,21(2):84-88.

[3] 黄淑女,杨承汉,谢伟峰.动态规划在成品油管道优化布站中的应用[J].油气储运,2005,24(7):6-9.

[4] 朱家松,龚健雅,郑皓.遗传算法在管网优化设计中的应用[J].武汉大学学报:信息科学版,2003,28(3):363-367.

[5] 杨筱蘅.输油管道设计与管理[M].东营:中国石油大学出版社,2006:272-283.

[6] 张红兵,卢亚萍.成品油管道工艺方案优化设计研究[J].石油工程建设,2008,34(3):20-23.

[7] 陈峰,张国忠.顺序输送管道变流速下混油量的计算方法[J].油气储运,2002,21(9):23-25.

[8] 陈庆勋.成品油顺序输送分输和变管径混油量的计算[J].油气储运,1999,18(1):7-8.

[9] 陈世一,崔艳星,崔艳雨.成品油顺序输送管道混油量计算方法[J].油气储运,2007,26(8):16-19.

[10] 雷英杰,张善文,李续武,等.MA TLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005:11-16.

(Ed.:W YX,Z)

M ixed Oil Influence Analysis in the Product Pipeline Netwo rk Op timal Design

FU Xiao-dong1,WANG Yue1,FU Ji-qang1,WANG Ai-ping2
(1.College of Petroleum Engineering,L iaoning Shihua University,Fushun L iaoning 113001,P.R.China; 2.School of Chem ical Engineering,Dalian University of Technology,Dalian L iaoning 116023,P.R.China)

7 M ay 2010;revised 25 June 2010;accepted 5 July 2010

Considered that the mixed oil would be p roduced in the batch transpo rtation of the p roduct oil pipeline,the highest revenue in the life cycle as the objective function,the diameter and the wall thickness as the decision variables,a p roduct pipeline network op timization model was set up.The calculation formula based on diffusion theory and empirical formula were used to calculatemixed oil quantity.And the genetic algo rithm was used to solve themodel.The results show that the design of mixed oil costs account fo r 3%to 10%,and it’s related to the factors as the transpo rtation batches per year,the number of species transpo rted in each batch and the cost on management of oilmixture per unit volume.Generally mixed oil loss can’t be ignored,and the weight coefficient method can be used for a variety of design options.Using different fo rmulation often got different result,so in p ractical engineering p rojects the closest fo rmulation can be chosen to calculate.

M ixed oil;Product oil;Pipeline network;Op timal design;MA TLAB;Genetic algorithm

.Te1.:+86-413-6861998;fax:+86-413-6861820;e-mail:fuxiaodong126@126.com

TE832

A

10.3696/j.issn.1006-396X.2010.03.021

1006-396X(2010)03-0090-04

2010-05-07

付晓东(1984-),男,河北任丘市,在读硕士。

辽宁省自然科学基金资助(20082186)。