北半球中低纬大气太阴潮汐对Es层的影响
2010-09-15牛晓娟赵光欣吕洪方
牛晓娟,赵光欣,吕洪方,柯 璇*
(1.江汉大学 物理与信息工程学院,湖北 武汉 430056;2.武汉纺织大学 理学院,湖北 武汉 430073)
北半球中低纬大气太阴潮汐对Es层的影响
牛晓娟1,赵光欣2,吕洪方1,柯 璇1*
(1.江汉大学 物理与信息工程学院,湖北 武汉 430056;2.武汉纺织大学 理学院,湖北 武汉 430073)
本文采用中低纬度数个台站的数字测高仪观测数据分析了Es层参数的大气太阴半日变化,结果表明:Es的临界频率(foEs)、遮蔽频率(fbEs)及虚高(h'Es)中均存在太阴半日周期的振荡。foEs和fbEs的太阴半日潮日变化及季节变化趋势非常相似,只是foEs太阴半日潮的幅度大于fbEs太阴半日潮的幅度,两者的相位几乎无差值。中低纬5个台站Es层参数的太阴半日潮幅度和相位的日变化值、季节变化值均不同,随纬度变化。foEs和h'Es的太阴半日潮存在年变化,在不同年份的相同月份,Es太阴半日潮的幅度和相位均有不同。值得提出的是我们还发现武汉foEs和h'Es的太阴半日潮最大值和武汉中层和低热层大气太阴半日潮汐风最大值出现的月份相同。
太阴潮汐;foEs;fbEs;h'Es
1 引言
大气太阴潮汐主要是太阴引潮力对低层大气的作用而引起的大气太阴周期性波动。潮汐波动通过动力学作用产生电流进而上传到电离层。这些电离层的电流引起的磁场导致在磁力计记录中存在太阴周期的信号。与此电流相对应的电场引起粒子漂移,也可以引起电离层Es层和F2层参数的变化。有关Es层参数的太阴变化已经有很多的报道[1-8],太阴潮汐对风剪切的影响在某种意义上体现在Es层的foEs、fbEs及h'Es的太阴潮汐特征上。Stening和Fejer[8]提到,在粒子漂移中探测到了太阴信号。电离层Es层和F2层的参数的太阴半日周期变化也被发现[10]。研究中层和低热层的大气太阴潮汐有助于我们了解当太阴潮在上传的过程中,中层的温度和风如何作用于它,进而推演中层大气的状态。同样,研究太阴潮汐对Es层的参数(foEs, fbEs,h'Es),在某种程度上有助于我们进一步完善风剪切理论[9]。近年来,人们对大气太阴潮的研究已经达到一定的高度,比较完善的太阴潮汐的模式也已经提出。在本文中,我们主要分析Wakkanai、Kokubunji、Yamagawa、 Wuhan 和 Okinawa这5个北半球的中低纬台站Es层参数的太阴半日潮的变化,并将观测的太阴潮的相位与GSWM模式[]的计算值作对比分析,进一步研究大气太阴潮汐对偶发E层的影响。
2 数据及分析方法
本文采用数据来自Wuhan观测台DGS256数字测高仪1999年4月27日到2004年8月17日期间将近6年的观测数据及日本的Wakkanai、Kokubunji、Yamagawa和Okinawa四个台站的数字测高仪数年的观测数据。表1分别给出所采用的这几个台站数据的年份。在数据分析过程中,我们首先对测高仪的数据做简单的处理,得到每个参数每日的小时均值。然后将这些参数的小时均值采用最小二乘法分析Es层的几个参数的太阴半日潮的变化特征。最小二乘法有一个最大的优点就是不要求一天的数据必须连续。
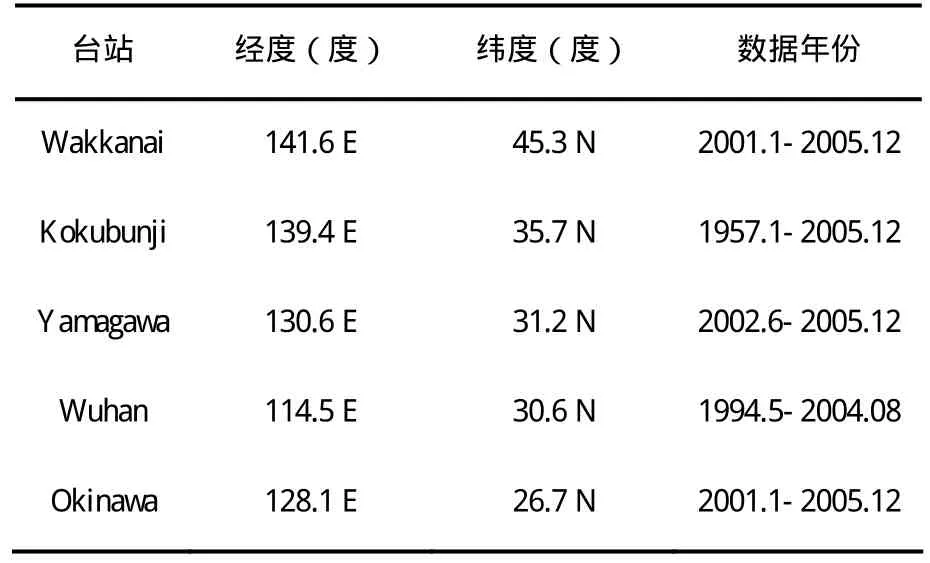
表1 采用数据的台站情况
3 观测结果
图1给出了Kokubunji 台站6月份Es层参数(foEs, fbEs和h'Es)的太阴半日潮日变化的幅度和相位。图1(a)是Es层foEs和fbEs的幅度和相位,(b)是foEs和h’Es的对比分析。为了方便比较,我们在做foEs和h’Es太阴潮幅度比较时,给foEs的幅度乘以10。在后面的对比分析中,foEs太阴潮的幅度均乘以10和h’Es的太阴潮幅度做比较。误差条代表正负一个标准偏差。如果太阴半日潮的幅度小于一个标准差,则其值和对应的相位不可信。由图可见,foEs和fbEs的太阴半日潮的周日幅度变化相似,都有明显的双峰出现,一个峰值出现在当地时3:00,另一个峰值出现在当地时18:00左右。两者相位的日变化趋势也非常相似,在5:00-13:00期间,它们之间的相位差值比较小。但foEs的太阴潮的幅度比fbEs太阴潮的幅度大。这和Tarpley和Matsushita[6]得到的太阴潮在foEs和fbEs的太阴潮的相位相似,foEs的太阴潮幅度比fbEs的幅度大的观点一致。分析表4.2的其他几个台站,h’Es太阴潮均在午后增强,foEs和h’Es的太阴潮的相位之间有明显的相位差。在多数时间,foEs的太阴潮相位滞后于h’Es的太阴潮相位,两者之间的相位差不稳定。
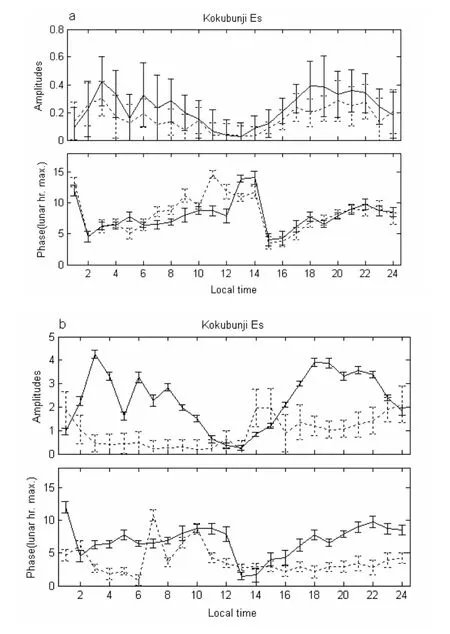
图1 Kokubunji 站6月份foEs, fbEs及h'Es的太阴半日潮日变化的幅度和相位,图(a、b)中实线均是foEs, (a)和(b)中的虚线分别是fbEs 和 h'Es。图(b)中的foEs太阴潮的幅度乘以10和h'Es的幅度比较。
3.1 季节变化
分析Kokubunji 站foEs、fbEs及h’Es的太阴潮的幅度和相位的季节变化(图2),其中图(a)是foEs和遮蔽频率的太阴潮季节变化的幅度和相位,图(b)是foEs和h’Es的。在Kokubunji站,foEs和fbEs的太阴潮的季节变化的幅度很相似,均在春秋季比较弱,在夏季特别强。foEs的太阴潮幅度比fbEs的大,两者的相位季节变化几乎完全相同。其他几个站的foEs和fbEs的太阴潮季节变化结果和Kokubunji站的一致,因此,后面的几个台站我们就只对foEs和h’Es的太阴潮的变化作对比分析。由图(b)可见,在2-4月份,h’Es的太阴潮比较弱,没有明显的夏季峰出现。foEs的相位滞后于h’Es的相位。在2-3月份,foEs和h’Es的相位都有个跳变。从4到11月份,两者的相位相对都比较稳定,随季节的变化不大。foEs的太阴潮平均相位约为7太阴时,但h’Es的太阴潮平均相位比foEs的超前4个太阴时左右,约为3太阴时。在多数月份,foEs的太阴潮相位和Matsushita的结论一致,但h’Es的太阴潮相位比其结果早约3个太阴时。
图3给出了同样位于北半球中纬地区的Wakkanai台站foEs和h’Es的太阴潮的季节变化。由图可见,Wakkanai的foEs的太阴潮在1、6及12月份都很强,但没有中纬Es明显的“夏季峰”出现。Es的h’Es的太阴潮在9月份幅度有最大值,Es的h’Es和foEs太阴潮间的相位差不稳定。在多数月份,Es的foEs的太阴潮相位滞后于h'Es的相位。Es的foEs的太阴潮相位随季节变化不是很明显,平均相位约为6太阴时。
图4-6分别给出了Yamagawa, Wuhan及Okinawa的Es层foEs及foEs和h’Es太阴潮汐季节变化的幅度和相位。在Yamagawa,foEs的太阴潮幅度最大值出现在8月份,h’Es的太阴潮在春季和9月份很强。在4、5、7和11月份,foEs的太阴潮相位滞后于h’Es的约3±1个太阴时。在1和8月份,两者的相位差达到6个太阴时左右。 在Wuhan,foEs的太阴潮幅度最大值出现在1和8月份,幅度值约为0.2MHz。与前面分析的Wuhan中层和低热层大气太阴半日潮最大值出现的月份一致[11,12],这可能是中层和低热层大气太阴潮上传到Es层所引起的结果。在2月份,h’Es的太阴潮很弱,3月份之后,h’Es的太阴潮几乎不随季节变化。在1-3月份和9-11月份期间,foEs和h’Es的太阴潮相位差为2个太阴时左右。在其他月份,两者之间的相位差比较大,且在多数月份,foEs的太阴潮相位仍然滞后于h’Es的。在Okinawa站,foEs的太阴潮在7、8月份很强,而h’Es的太阴潮在5到9月份都比较弱。h’Es的太阴潮在4月份最强,幅度值超过2 km。除过1和9月份,其他月份的foEs的太阴潮相位都滞后于h’Es的。两者之间的相位差不稳定,例如在9月份相差几乎为零,但在7月份相差为6个太阴时左右。
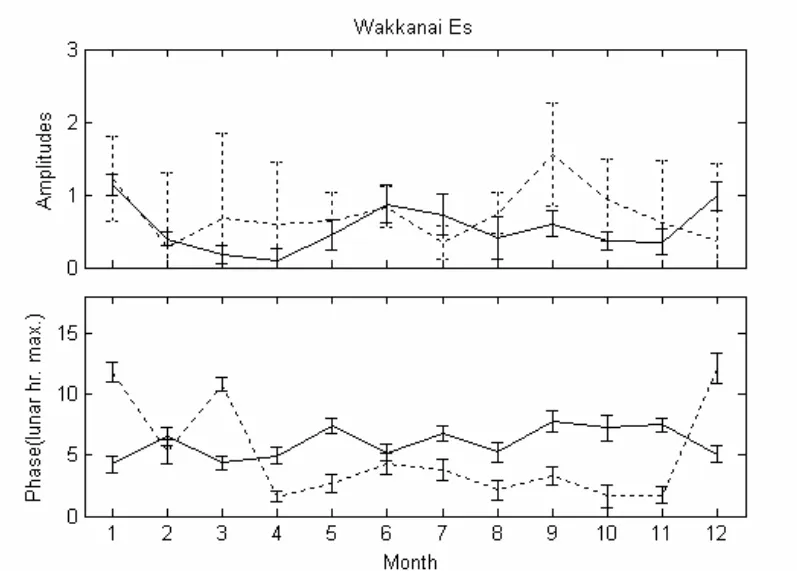
图 3 Wakkanai站foEs及h'Es的太阴潮的季节变化,实线是foEs,虚线是h'Es。图中的foEs太阴潮的幅度是乘10的结果
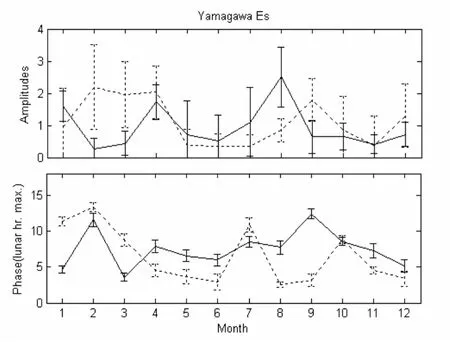
图4同图3,但是Yamagawa的EsfoEs和h’Es的太阴潮的季节变化
上面提到的5个台站,都位于北半球的中低纬地区,对比分析这5个台站Es层参数太阴潮的季节变化。图7给出了这5个台站foEs的太阴潮在12个月份的幅度和相位。由图可见,除过纬度相对较高的Wakkanai站之外,其他4个台站foEs的太阴潮均在1月份和8月份相对比较强。而Wakkanai站在1和6月份比较强。foEs的太阴潮相位的季节变化有差异,但在多数月份,5个台站之间的相位差很小,且平均相位约为5太阴时左右。
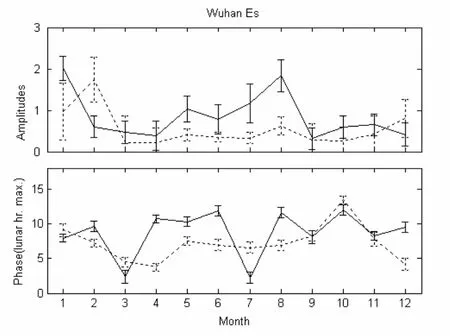
图 5 同图3, 但是Wuhan的EsfoEs和h’Es的太阴潮的季节变化
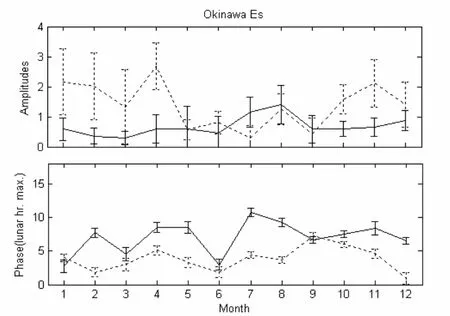
图 6 同图3, 但是Okinawa的EsfoEs和h’Es的太阴潮的季节变化
图8给出了这5个台站h’Es的太阴潮季节变化。由图可见,同月份、不同纬度的5个台站h’Es的太阴潮的幅度值不同,但均在5-7月份之间比较弱。各个台站的h’Es的太阴潮相位季节变化也不相同,但在大多数月份,相位在4太阴时左右随季节变化。Es参数的太阴潮不仅有季节变化,还随纬度变化。
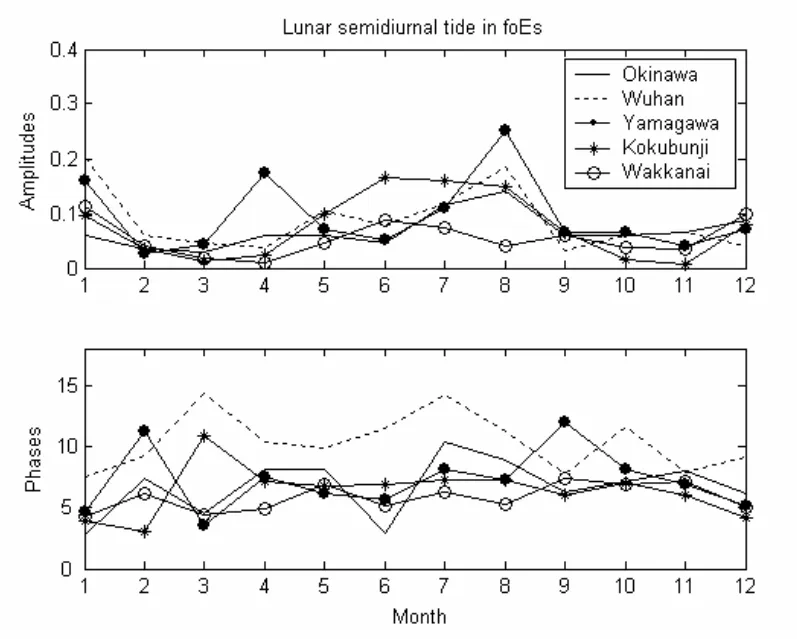
图 7 纬度相近的Kokubunji、Wakkanai、Yamagawa, Wuhan及Okinawa 5个台站的EsfoEs的季节变化比较
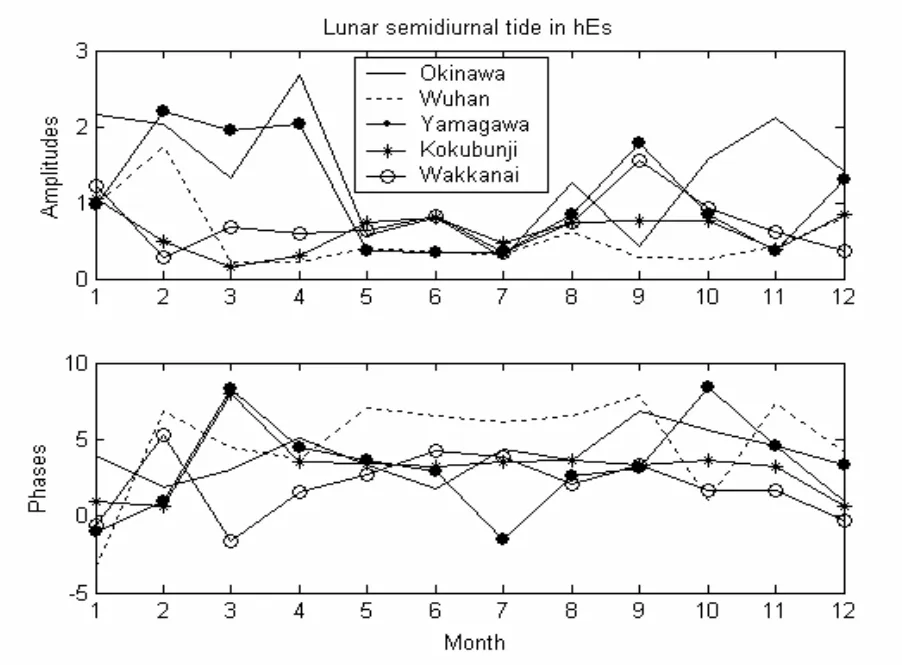
图 8 同图7,但是5个台站的Esh’Es的季节变化比较
3.2 年变化
在分析Es参数的太阴变化时均采用将数年的数据一起分析,得到的是一个平均结果。那么这些参数的太阴潮究竟有没有年变化呢?我们选择观测数据比较长的Kokubunji站分析Es参数太阴潮的年变化。图9和10分别给出了Kokubunji站6月份和12月份 foEs和h’Es的年变化。选取Kokubunji站1960年到2004年45年的数据,每5年的数据为一组(如1960到1964年6月份的数据一起求得1960年6月份Es太阴潮的幅度和相位),用最小二乘法分析得到该站foEs和h’Es的太阴潮年变化的幅度和相位。同样,将45年的数据一起采用最小二乘法也可以求得45年的平均foEs和h’Es太阴潮年变化的幅度和相位。分别选取6月份和12月份foEs和h’Es的太阴潮不同年份的幅度和相位做比较分析(图9-10),同时,图中也给出了45年的数据一起求得的平均的太阴潮的幅度和相位。由图9可以看到,Kokubunji站6月份foEs和h’Es的太阴潮的幅度和相位均有年变化,且幅度的年变化比较明显。如除过1985和2000的foEs的太阴潮的幅度小,且误差很大,其对应的相位不可信。从1975到2000年,foEs的太阴潮幅度偏离平均值比较大。在1975,1980,1990和1995四段时间,foEs的太阴潮明显强于其他年份。h’Es的太阴潮的幅度也存在小的年变化,基本上围绕平均值做小的变化。而foEs和h’Es的太阴潮相位随不同年份的变化相对比较小,foEs的太阴潮相位围绕6太阴时做小幅度的变化,h’Es的太阴潮相位的均值约为3太阴时。foEs的太阴潮相位滞后于h’Es的约3个太阴时。在12月份,foEs和h’Es的太阴潮的幅度年变化趋势非常相似。在1960和1965的年份里,foEs和h’Es的太阴潮均比其他年份强。foEs的太阴潮的幅度年变化很明显,在多数年份,比平均值大,而foEs的相位随年份的变化不大,相位均值约为4.5太阴时。h’Es的太阴潮的幅度也存在年变化,但基本在平均值附近做小的变化。h’Es的太阴潮的相位在1970-1980之间,相位大于平均相位,随年份逐年变化,在其他年份,相位值和平均值很接近。在12月份,foEs的相位仍滞后于h’Es的相位,两者之间的相位差值不稳定。Townsville的Es层太阴潮的相位分析也表现出年变化,但是年和年之间还是存在一定的连贯性[13-14]。在许多台站中层和低热层大气太阴潮汐的分析中发现,大气太阴潮汐风有年变化的特点[15]。对于较长时间的数据序列,年变化就可能被平均掉。
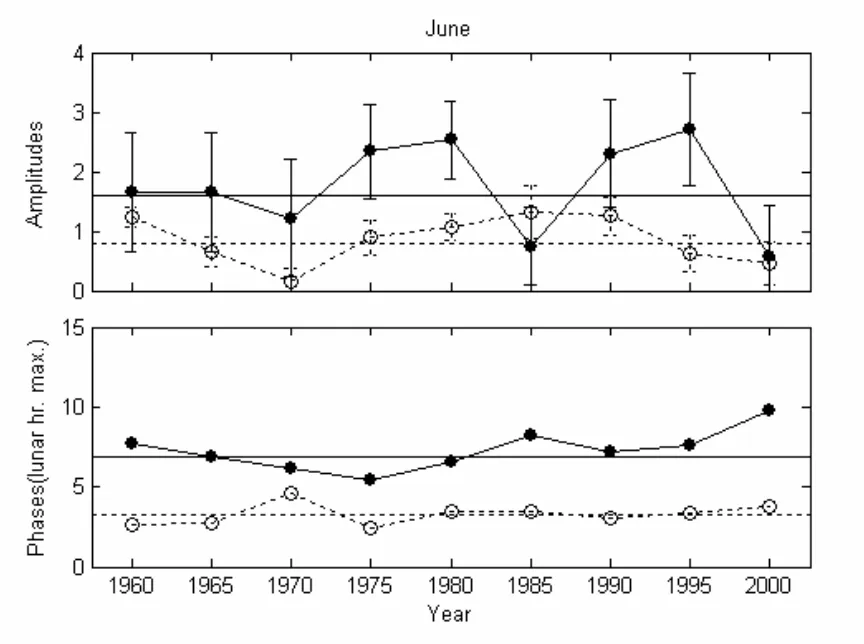
图9 Kokubunji站6月份 foEs和h’Es的太阴潮在不同年份的幅度和相位变化。图中的直线代表1960-2004年所有数据一起计算的结果,其中实线表示foEs,虚线表示h’Es。图中的foEs太阴潮的幅度是10倍的foEs太阴潮的幅度
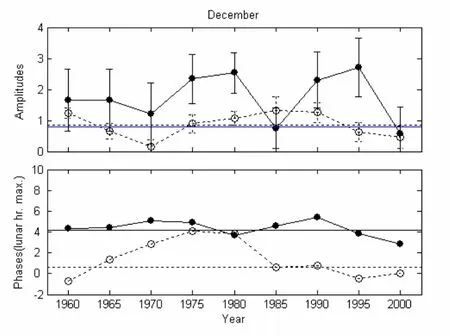
图10 同图9,但是12月份的结果
4 讨论与小结
本文分析了Es的几个参数的太阴半日潮的日变化、季节变化和年变化,得到foEs和fbEs太阴潮的相位几乎一致,但foEs太阴潮的幅度比fbEs的大。这可能是因为fbEs和foEs的性质不同[7]。Es的火箭和测高仪的同期观测表明,foEs是Es层等离子体频率的最好指数,而fbEs比等离子体频率大百分之几到百分之五十[16]。且计算表明,从电子浓度梯度的部分反射和小尺度电子密度的不规则散射产生高的foEs值。Matsushita对Es层太阴潮汐的观测总结发现,在多次观测中,foEs的太阴最大时间在7h左右,而h’Es比它早一个太阴时,大约在6h左右[1]。本文的观测表现出和Matsushita不完全相同的结果,h’Es的太阴潮相位比foEs的滞后约4个太阴时左右。在Darwin,foEs的太阴潮相位有4个月中表现出滞后于h’Es的约3小时左右,在赤道附近的Vanimo,从9到2月份,foEs的太阴潮相位和h’Es的之间存在3±1.5h的相位差[7]。Stening还提到,一般中性风随高度的变化是一个垂直波长约为20 km的类正弦曲线。假设太阴潮汐风叠加在这个曲线上,而太阴半日潮汐预期的垂直波长较长,约为60-70 km。当太阴潮汐东向达到最大时,它将取代整个东向曲线。这样就抬高了风转向的高度。因而断定,当太阴潮汐东向达最大时,h’Es的太阴潮汐也将达最大值。因此,当风剪切理论成立时,太阴东向风和h’Es的最大时间应该一致。而决定Es强度的主要因子包括背景粒子浓度、存在的重粒子数量和风剪切的强度。所以foEs的最大值出现的时间可能与这些因素有关。另外,Es层高度上的foEs和h’Es这两个参数,在不同的当地时可能不同,因而他们的中性大气太阴潮汐表现的特征也不同。
由风剪切理论我们知道,当在某一个高度上存在东向风,而略高一点的高度上存在西向风,就造成一个风剪切。上面的离子向下运动,下面的离子向上运动,电离成份得到有效压缩。因此,为了进一步检验我们的理论,我们需要确定电离层E区东向的太阴潮汐风。因为Es层的层高每天都在变化,而且风的相位也随高度变化。首先我们需要知道测量那个高度的中性太阴潮汐风的相位。图11给出了GSWM模式计算出的北纬30度处的Wuhan站6月份96-142 km高度范围的东向太阴半日潮的幅度和相位的高度变化剖面。由图可见,Wuhan太阴潮汐风的东向分量在110 km左右的高度达到最大值。因而我们首先需要求得Es层的平均高度,用这个平均高度去确定风的相位并和模式计算的相位比较。
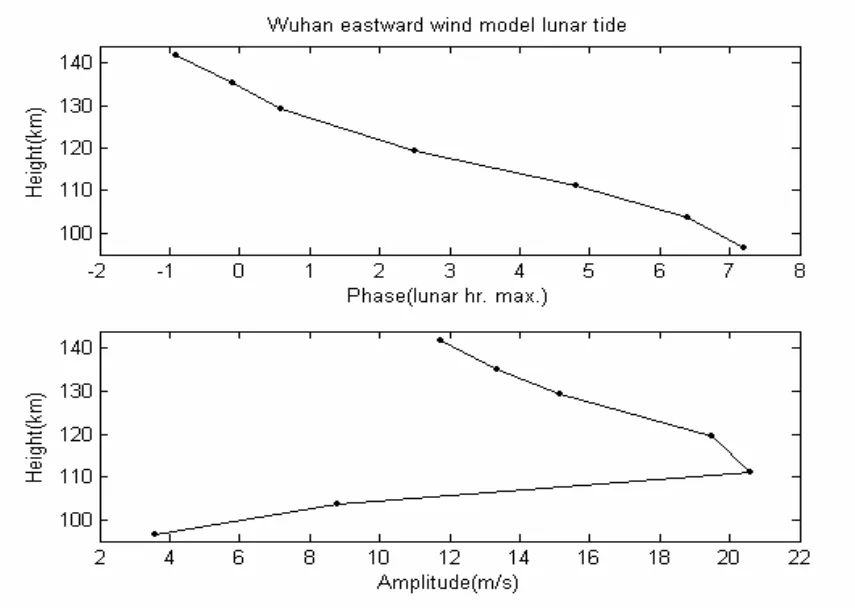
图11 GSWM模式计算出的Wuhan6月份东向太阴潮汐风的相位和幅度
表2给出了上面提到的5个台站Es层参数的太阴变化的相位和模式的东向分量的相位的详细对比结果。在进行比较时,我们选取Es层的太阴潮比较强,幅度值可信的月份做比较。高度选取的是此年此月份Es的观测高度的平均值。在这个高度的太阴东向分量最大值出现的时间来自于各台站相对应纬度的GSWM的计算结果。当我们的计算值和模式的值之间的相差在2太阴时内,我们认为和风剪切理论一致(Stening,1999)。在表2的数据分析中我们得到,16个结果中有14个一致,所占百分比为87.5 %,与风剪切理论符合的相当好。
Es的foEs、fbEsfbEs及h’Es的太阴潮的日变化各个台站不同,但在中纬台站foEs和fbEs的太阴潮的日变化趋势非常相似,只是foEs的太阴潮幅度大于fbEs的,两者之间的相位几乎无差值。Kokubunji站foEs和fbEs的太阴半日潮的日幅度变化相似,都有明显的双峰出现,一个峰值出现在当地时3点,另一个峰值出现在当地时18点左右。而h’Es的太阴潮在午后增强,foEs和h’Es的太阴潮的相位之间有明显的相位差。在多数时间,foEs的相位滞后于h’Es的相位,两者相差不稳定。
同样,在北半球中纬的几个台站的结果表明,中纬地区foEs的太阴潮幅度比fbEs的大,而两者的相位季节变化几乎完全相同。除过纬度相对较高的Wakkanai站之外,其他4个台站均在1月份和8月份相对比较强。Wakkanai站在6和1月份比较强。foEs的太阴潮相位的季节变化有差异,但在多数月份,5个台站之间的相位差很小,且平均相位约为5太阴时左右。在不同纬度的各个台站的h’Es的太阴潮的季节变化表现不同,但均在5-7月份之间比较弱。各个台站h’Es的太阴潮相位季节变化也不相同,但是在大多数月份,相位围绕在4太阴时左右随季节变化。Es参数的太阴潮不仅有季节变化,还随纬度变化。另外,由武汉站的中层和低热层大气太阴半日潮和武汉Es层foEs及h’Es的太阴半日潮最大值出现的月份一致,可以得到,低层大气太阴潮汐上传,可能对Es层产生太阴周期性的影响。中纬台站foEs和h’Es的太阴潮存在年变化,在不同年份的相同月份,Es太阴潮的幅度和相位均有不同。从GSWM模式计算的太阴潮的相位与几个中纬度台站的Es参数太阴变化的相位的比较来看,在大多数情况下,Es的出现符合风剪切理论。
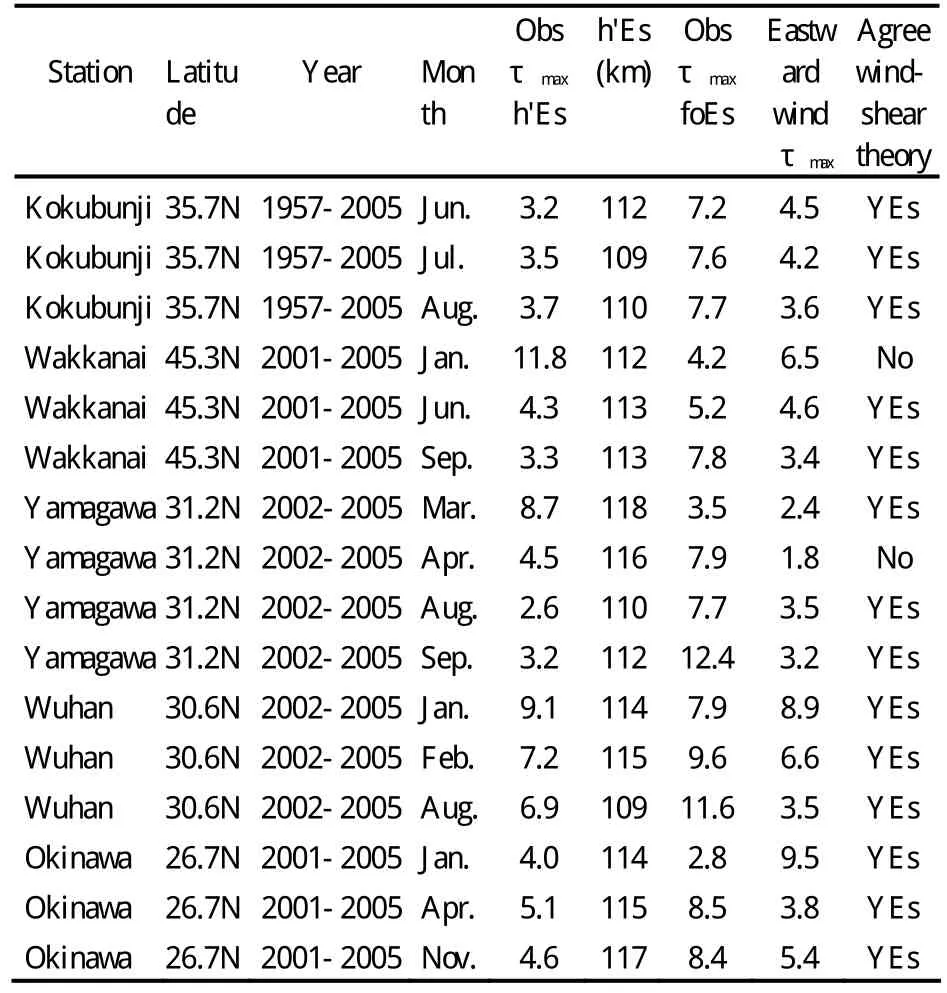
表2 5个台站Es层参数的太阴变化的相位和模式的东向分量的相位对比结果
[1] Matsushita S. Lunar tidal variations in the sporadic-E region[J]. Rep. Ionos. Res. Jap., 1953, (7): 45-52.
[2] Thomas J A. Svenson A C. Lunar tide in sporadic E at Brisbane[J]. Aust. J. Phys., 1955, (8): 554-556.
[3] Swarm H M. Helliwell R A. Lunar tidal variations in the sporadic-E layer of the ionosphere at Stanford[C]. California, presented at USNC/URSI-IRE Fall Meeting, 1956.
[4] Wright R W. Skinner N J. Lunar tides in the sporadic E layer at Ibadan[J]. J. Atmos. Terr. Phys., 1959, (13): 217-221.
[5] Joshi B K. Kotadia K M. Lunar tidal variations in the equatorial sporadic-E layer[J]. J. Atmos. Terr. Phys., 1970, (32):1057-1066.
[6] Tarpley J D. Matsushita S. The lunar tide in fbEs[J]. Radio Sci., 1971, (6): 191-196.
[7] Stening R. J. The lunar tide in sporadic E[J]. Ann. Geophys., 1999, (17):1344-1351.
[8] Standford D J. Mitchell N J. Vincent R A. etl. The lunar tides in the Antarctic mesosphere and lower thermosphere[J]. J. Atmos. Terr. Phys., 2007,(69):2219-2237.
[9] Stening R J. Fejer B G.. Lunar tide in the equatorial F region vertical ion drift velocity[J]. J. Geophys. Res., 2001, (106): 221-226.
[10] Stening, R J. Richmond A D. Roble R G.. Lunar tides in Thermosphere-Ionosphere-Electrodynamics General Circulation Model[J]. J. Geophys. Res., 1999,(104):1-13.
[11] Niu X J. Xiong J G. Wan W X. etl. Lunar tidal winds in the mesosphere over Wuhan and Adelaide[J]. Adv. Space Res., 2005, (36): 2218-2222.
[12] Niu X J. Xiong J G. Wan W X. etl. A measurement of lunar semidiurnal tide at Wuhan(30o40’N, 114o30’E) [J]. Earth Planets and Space, 2007, (59): 991-997.
[13] Stening R. Tsuda J T. Nakamura T. Lunar tidal winds in the upper atmosphere over Jakarta[J]. J. Geophys. Res., 2003, (108): 1192-1199.
[14] Stening, R J. Richmond A D. Roble R G.. Lunar tides in the Thermosphere-Ionosphere-Electrodynamics General Circulation Model[J]. J. Geophys. Res., 1999,(104):1-13.
[15] Stening, R J. Manson A H. Meek C E. etl. Vincent, Lunar tidal winds at Adelaide and Saskatoon at 80 to 100 km heights: 1985-1990[J]. J. Geophys. Res., 1994, (99):13273-13280.
[16] Reddy C A. Physical significance of the Es parameters fbEs, fEs and foEs, 2, Causes of partial reflections from Es[J]. J. Geophys. Res., 1968, (73): 5627-5647.
Effects on Sporadic E Layer of the Lunar Atmosphere Tide at Middle Latitudes in The Northern Hemisphere
NIU Xiao-Juan1, ZHAO Guang-Xin2, LÜ Hong-Fang1, KE Xuan1
(1. School of Physics & Information Engineering, JiangHan University ,Wuhan Hubei 430056, China; 2. School of science, Wuhan Textile University, Wuhan Hubei 430073, China)
Using the data of several ionosondes, the influence of lunar atmosphere to Es-layer is analyzed in this paper. It showed: there is lunar semidiurnal oscillation in the critical frequency (foEs), blanketing frequency (fbEs) and virtual height (h'Es) of Es-layer. The diurnal and seasonal variations of lunar tide in foEs and fbEs are very similar except the amplitude of foEs is bigger than the fbEs one. The phase’s difference of foEs and fbEs is very small. The diurnal and seasonal variations of lunar semidiurnal tide in Es are different in five stations of low-middle latitude in northern hemisphere. It varies with latitude. Both the foEs and h'Es of the lunar semidiurnal tide have year-to-year variation. At same month in different years, the amplitude and phase of the lunar semidiurnal tide in Es maybe different. It should be to point out that the lunar semidiurnal tide in Es and at MLT region in Wuhan station reach the maximum values in the same month.
lunar atmosphere tide; foes; fbEs; h'Es
P352.4
A
1009-5160(2010)03-0022-07
*通讯作者:柯璇(1963-),男,副教授,研究方向:计算物理.
国家自然科学基金(40804038);湖北省科技攻关计划项目(2005AA101C56).
