光纤LP01模远场发散角与归一化频率关系的研究
2010-09-15胡林顺李连煌郭福源
胡林顺,李连煌,郭福源
(1. 五邑大学 应用物理与材料学院,广东 江门 529020;2. 福建师范大学 激光与光电子技术研究所,福建 福州 350007)
光纤LP01模远场发散角与归一化频率关系的研究
胡林顺1,2,李连煌2,郭福源2
(1. 五邑大学 应用物理与材料学院,广东 江门 529020;2. 福建师范大学 激光与光电子技术研究所,福建 福州 350007)
根据折射率阶跃对称分布的光纤LP01模端面衍射远场的振幅分布,分析了衍射光束的半值全角宽度及振幅下降到1/e处对应的远场发散角全角各自随光纤归一化频率变化的关系;采用等效匹配效率法分析了远场发散角角半径,拟合出远场发散角角半径随归一化频率变化的函数表达式,并通过误差分析证明了拟合函数表达式的精确性.
远场发散角;半值全角宽度;等效匹配效率法;相对误差
评价和描述光纤激光器光束的方法有许多,例如采用远场发散角、光斑半径及模式等,根据不同的定义即使同一参数也会有不同的结论,因此在实际应用中很难做出选择. Petermann K[1-2]根据光纤LP01模衍射远场的振幅分布,给出了光纤远场发散角的第一、第二定义,即二阶矩远场发散角和微分算子远场发散角,它们被广泛用于光纤出射光束的分析计算[3-7]. 本文根据折射率阶跃对称分布的光纤 LP01模端面衍射远场的振幅分布[8],参考高斯光束远场发散角的定义[9],分析了衍射光束的远场发散角与光纤归一化频率的关系,并建立数学模型拟合得出其近似函数表达式. 因为二阶矩算法和微分算子算法定义的远场发散角角半径存在一定的差异,所以本文采用等效匹配效率法[10]分析远场发散角角半径.
1 半值全角宽度
当端面不受限时,折射率阶跃对称分布的光纤LP01模衍射远场振幅分布的函数表达式为[8]282

式中:F=kasinθ为空间频率;U为光纤芯层驻波参量;W为光纤包层倏逝波参量;v为光纤归一化频率,v=,它包含了光纤的基本结构参数芯层半径a、芯层折射率n1和包层折射率n2.由式(1)可知,光纤 LP01模端面不受限衍射光束远场的振幅分布S(θ)与光纤归一化频率v、光纤芯层驻波参量U、光纤包层倏逝波参量W有关.
参考高斯光束远场发散角的定义之一:衍射光束远场振幅下降到中心最大值 1/2处与z轴的夹角即为半值全角宽度. 由式(1)可得光纤 LP01模衍射光束的半值全角宽度θFWHM与光纤归一化频率v的关系,如图1所示.由图1中的实线可知:光纤LP01模端面无受限衍射光束的半值全角宽度θFWHM随光纤归一化频率v的增大而单调递增.

图1 半值全角宽度与光纤归一化频率v的关系曲线
为了确定半值全角宽度与光纤归一化频率的函数关系,分析实际曲线建立如下数学模型:

式中a、b、c、d为待定系数. 取实线上的4个点(1, 0.016 56),(5, 0.252 2),(10, 0.297 7),(25, 0.321 5)代入式(2)计算可得:a=-0.919 9,b=1.06 7,c=0.538 3,d=0.322 5,即半值全角宽度与光纤归一化频率的拟合函数关系可表示为

由式(3)可得图1所示的虚线. 由图 1可知:虚线与实线基本重合,即由式(3)近似表达的半值全角宽度与光纤归一化频率v的函数关系和实际情况吻合.
为详细分析拟合曲线的精度,需计算出拟合远场发散角的相对误差,相对误差的通用表达式

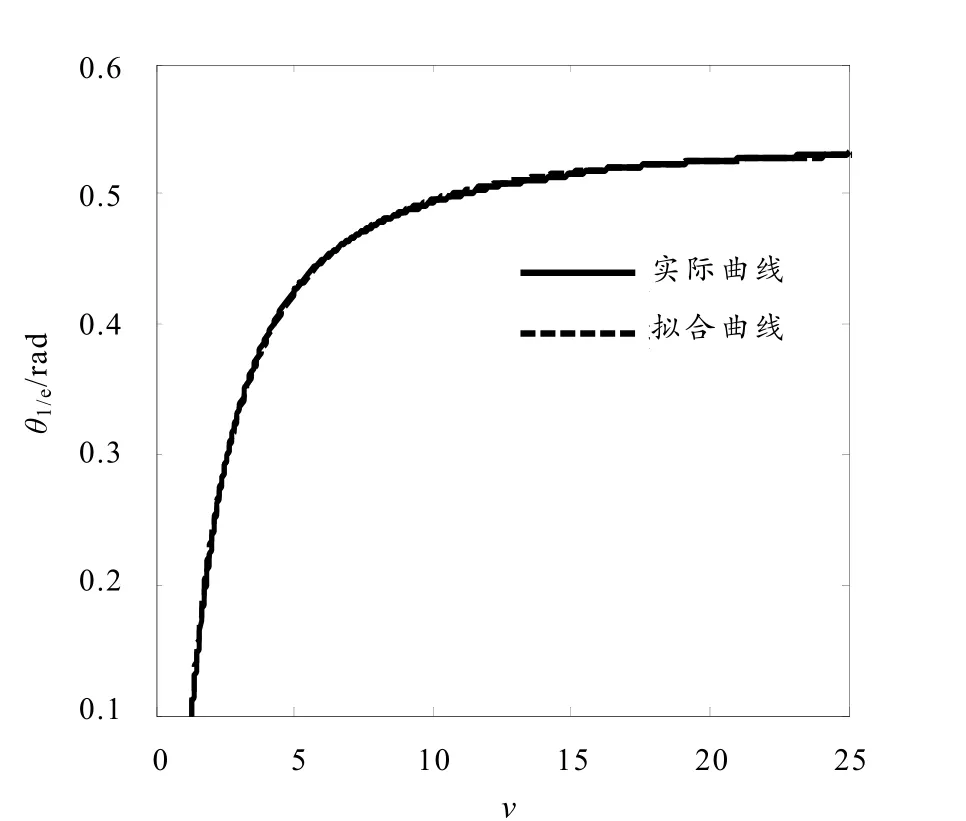
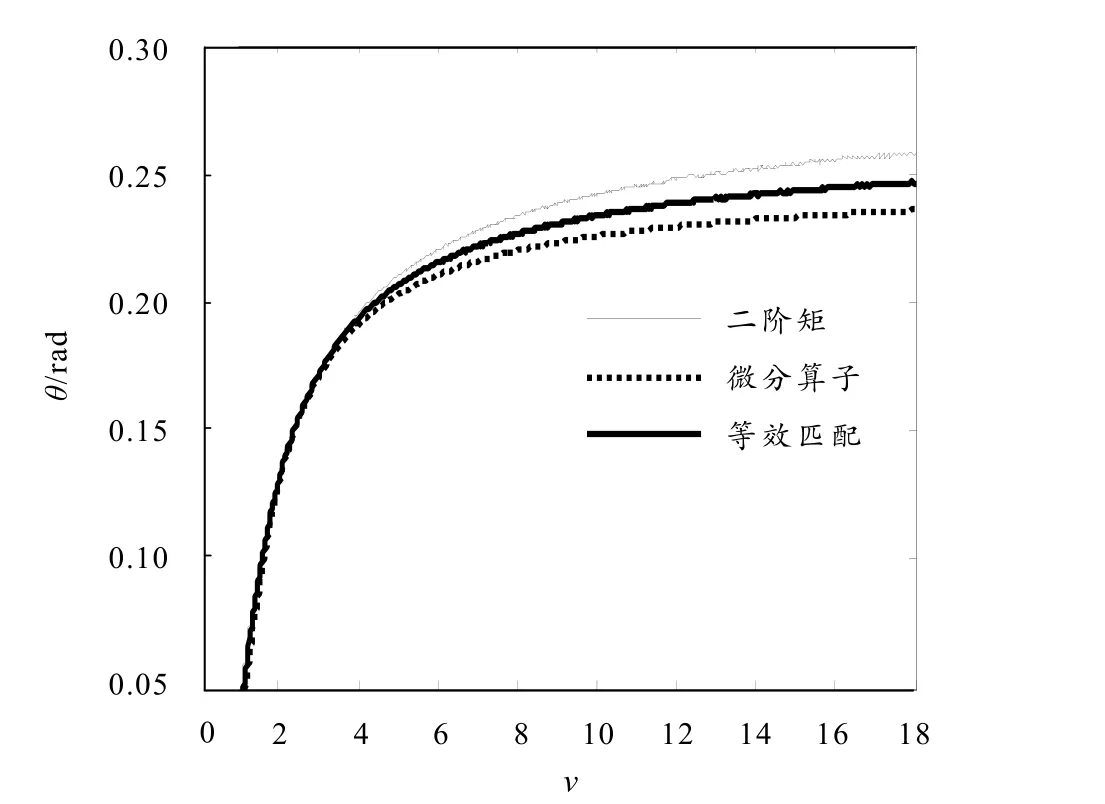
式中,θ为实际远场发散角,θ′为拟合远场发散角. 由式(3)、(4)可计算其相对误差,当 2 高斯光束远场发散角半角的一般定义:远场高斯光束振幅下降到中心最大值1/e处与z轴的夹角,其对应的束内功率为 86.5%[9]64. 常用远场发散角全角θ1/e作为描述和评价衍射光束的参量之一. 参考高斯光束远场发散角全角θ1/e的定义,由式(1)可得出光纤LP01模远场发散角全角θ1/e随光纤归一化频率v变化的关系,如图 2所示.由图 2实线可知:光纤远场发散角全角θ1/e随光纤归一化频率v的增大而单调递增. 当 1 (4)煤泥回收能力偏低,严重制约重介质选煤生产。主要表现在脱水设备老化,不能及时有效回收浮选精矿,从而制约浮选正常生产,并且由于浮选精煤水分偏高对外销造成了不利影响;尾煤泥不能有效回收,导致循环水浓度增高,从而影响整个洗煤生产。 图2 远场发散角全角与光纤归一化频率v的关系曲线 采用式(2)的指数函数拟合图2中的实线,取实线上的4个点(1.5, 0.152),(5, 0.422 9),(10, 0.494 8),(25,0.529 5)代入式(2)计算得:a=-3.011,b=1.76,c=0.386 8,d=0.536 2,即远场发散角全角θ1′/e与光纤归一化频率v的函数关系式 由式(5)可得图2所示的虚线. 由图2可知:由式(5)描述的远场发散角全角与光纤归一化频率v的函数关系与实际情况吻合. 为了定量分析拟合函数关系表达式的精确度,需计算出拟合远场发散角全角的相对误差,当 1 根据定义Petermann I和Petermann II计算光纤远场发散角角半径,即二阶矩远场发散角角半径和微分算子远场发散角角半径,它们的表达式分别为 由式(1)、(6)和(7)可得二阶矩远场发散角角半径θSM和微分算子远场发散角角半径θDO与光纤归一化频率v的关系,如图3所示. 由图3可知:二阶矩远场发散角角半径θSM、微分算子远场发散角角半径θDO随着光纤归一化频率v的增大差异越来越大;因此本文采用等效匹配效率法计算光纤远场发散角角半径θeq,即 由式(8)可得等效匹配效率远场发散角角半径θeq随光纤归一化频率v的变化关系,如图3所示. 由图3知:等效匹配远场发散角角半径θeq介于二阶矩发散角角半径θSM和微分算子发散角角半径θDO之间,且随光纤归一化频率v的增大而单调递增.当1 为评价3种远场发散角角半经,需计算它们各自拟合得到的高斯近似分布与实际振幅场分布的匹配效率,表达式[11]为 图3 远场发散角角半径与光纤归一化频率v的关系曲线 图4 等效匹配效率远场发散角角半径与光纤归一化频率v的关系曲线 式中:SG(θ)为高斯近似衍射光束的远场空间频谱分布;Sreal(θ)为实际衍射光束的远场空间频谱分布. 以v=2为例,由式(9)可得二阶矩高斯近似衍射场分布、微分算子高斯近似衍射场分布、等效匹配效率高斯近似衍射场分布分别与实际衍射场分布的匹配效率为:ηSM=99.86%,ηDO=99.83%,ηeq=99.93%. 结果表明:等效匹配效率法优于二阶矩算法和微分算子算法. 为明确等效匹配效率远场发散角角半径θeq与光纤归一化频率v的函数关系,采用指数函数式(2)拟合图3中的粗实线. 取粗实线上4个点(1.5, 0.094 62),(5, 0.206 1),(10, 0.234 4),(18, 0.245 4)代入式(2)计算得:a=-2.077,b=2.263,c=0.324 5,d=0.251 8,因此拟合的等效匹配效率远场发散角角半径θe′q与光纤归一化频率v的函数关系表达式 由式(10)可得拟合的等效匹配效率远场发散角角半径θe′q随光纤归一化频率v的变化关系(图4中虚线). 由式(10)、(4)计算出拟合的等效匹配效率远场发散角角半径θe′q与实际的等效匹配效率远场发散角角半径θeq的相对误差绝对值小于 2%. 结果说明:拟合函数表达式(10)描述的等效匹配效率远场发散角角半径与实际情况基本吻合. 本文根据光纤 LP01模端面无受限衍射远场振幅分布的解析函数表达式计算出衍射光束的半值全角宽度和振幅下降到 1/e处所对应的远场发散角全角各自随光纤归一化频率变化的函数关系;采用等效匹配效率法得出远场发散角角半径随光纤归一化频率变化的关系,用指数函数y=aexp(−bxc)+d进行曲线拟合,并通过相对误差分析了拟合函数表达式的精确度,结果表明:拟合得到的函数表达式能很好地描述实际情况,方便工程实际应用. [1]PETERMANN K. Fundamental mode microbending loss in graded-index andWfibers [J]. Optical and Quantum Electronics, 1977, 9(2): 167-175. [2]PETERMANN K. Constraints for fundamental-mode spot size for broadband dispersion-compensated singlemode fibers [J]. Electronics Letters, 1983, 19(18): 712-714. [3]ARTIGLIA M, COPPA G, VITA P D, et al. Mode field diameter measurements in single-mode optical fibers [J]. Journal of Lightwave Technology, 1989, 7(8): 1 139-1 152. [4]THIRUMENI S, POOPALAN P, HASSAN A A, et al. Effects of scan angles in the far-field scanning method on the measurement of the mode field diameter[C]//Proceedings of IEEE International Conference on Semiconductor Electronics, New Jersey: IEEE Service Center, 1998, 121-123. [5]LI Lianhuang, GUO Fuyuan, WANG Lixiang, et al. Relationship between the beam parameters and structure parameters of single mode fiber [J]. Acta Photonica Sinica, 2007, 36(7): 1 219-1 223. [6]李连煌,郭福源,胡林顺,等. 平面波导基模端面衍射光束参量与波导结构参数关系的研究[J]. 福建师范大学学报:自然科学版,2007, 23(2): 45-48. [7]LIN Bin, WEN Xuejin, GUO Fuyuan. Influence of cladding layer field of slab waveguide onM2factor [J]. Chinese Optics Letters, 2003, 1(8): 441-443. [8]郭福源,林斌,陈钰清,等. 光纤端面衍射场光束的特征参数[J]. 浙江大学学报:工学版,2004, 38(3): 1 281-285. [9]吕百达. 激光光学:光束描述、传输变换与光腔技术物理[M]. 3版. 北京:高等教育出版社,2003. [10]LI Lianhuang, GUO Fuyuan, GAO Rui, et al. Analysis on the Gaussian approximation of LP01mode[C]// 1 Proceedings of SPIE, Beijing: [s.n.], 2007, 2: 6 837. [11]叶培大,吴彝尊. 光波导技术基础理论[M]. 北京:人民邮电出版社,1981. [责任编辑:孙建平] Research on the Relationship Between Divergence Angles of Fiber LP01Mode and Normalized Frequency HU Lin-shun1,2, LI Lian-huang2, GUO Fu-yuan2 Based on the far-field diffraction amplitude distribution of fiber LP01mode, the relationships between full angle at half maximum and the far-field divergence full angle of the amplitude drop to 1/e point with fiber normalized frequency are analyzed. The equivalent matching efficiency method is employed for the calculation of far-field divergence angle, and the function expression of the angle along with the fiber normalized frequency is fitted, and its accuracy is proved through error analysis. far field divergence angle; full angle at half maximum; equivalent matching efficiency method; relative error TN25;O436 A 1006-7302(2010)02-0005-24 2010-01-11 福建省科技厅F5类项目(2007F5040);福建省自然科学基金资助项目(A0540001) 胡林顺(1983—),男,江西吉安人,实验师,硕士,研究方向:光纤和激光光束质量,E-mail: hulinshun@yahoo.com.cn.2 振幅下降到1/e处的远场发散角全角

3 等效匹配远场发散角角半径
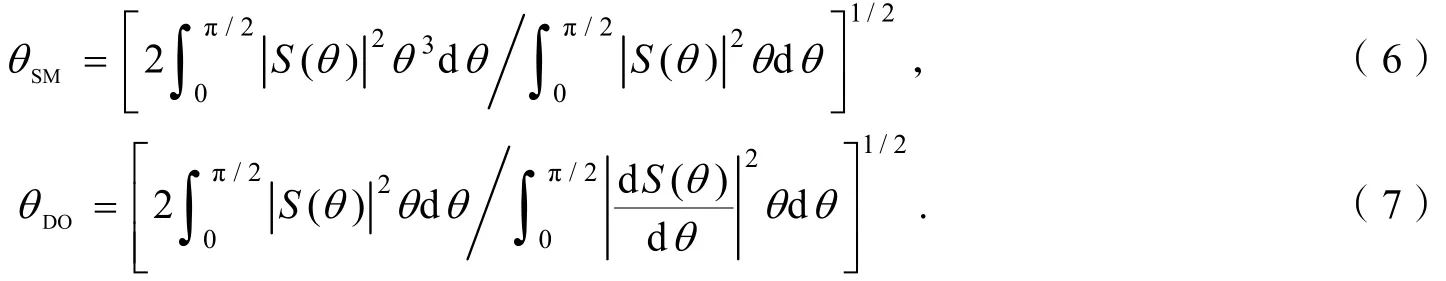

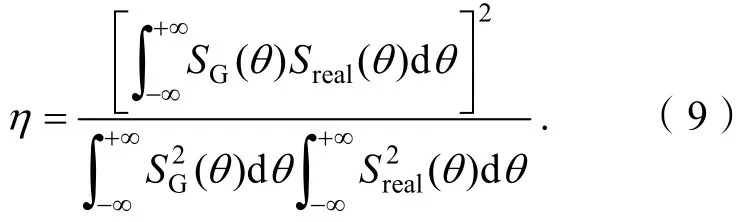

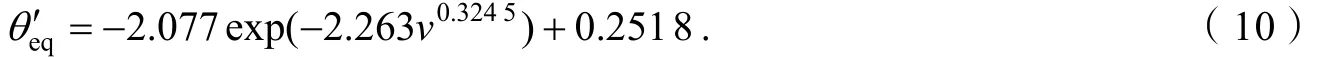
4 结论
(1. School of Applied Physics & Materials Engineering, Wuyi University, Jiangmen 529020, China; 2. Institute of Laser & Optoelectronics Technology, Fujian Normal University, Fuzhou 350007, China)
