下承式钢管混凝土拱桥稳定分析＊

吴海军,邹 魁,余 朝

(1.湖南省交通科学研究院,湖南长沙 410015;2.湖南中大设计院有限公司,湖南长沙 410075; 3.中南大学交通运输工程学院,湖南长沙 410075)

下承式钢管混凝土拱桥稳定分析＊

吴海军1,邹 魁2,余 朝3

(1.湖南省交通科学研究院,湖南长沙 410015;2.湖南中大设计院有限公司,湖南长沙 410075; 3.中南大学交通运输工程学院,湖南长沙 410075)

通过工程实例,介绍了下承式钢管混凝土拱桥稳定性分析方法,包括线性和非线性。利用有限元理论,建立了此钢管混凝土拱桥计算模型;运用ANSYS软件对该桥线性和非线性稳定进行了模拟计算,得出安全稳定系数,其结果为该桥的设计提供了依据。

钢管混凝土拱桥;线性;非线性;稳定分析;ANSYS

一、计算分析要点及内容

(1)线弹性稳定分析:将结构外力作为荷载进行静力分析,获得此时的内力状态;再进行特征值分析,得到最小特征值作为第一类稳定安全系数即失稳临界荷载系数;在临界荷载下,拱桥结构线性分析的平衡方程为:

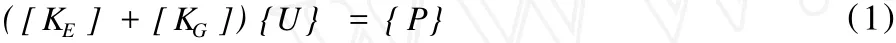
式中,[KE]为结构的弹性刚度矩阵;[KG]为结构的几何刚度矩阵,也称为初应力刚度矩阵;{U)为节点位移向量;{P}为节点荷载向量。上式也是几何非线性分析的平衡方程。

为得到所遇平衡状态,应使系统势能的二阶变分为零,即

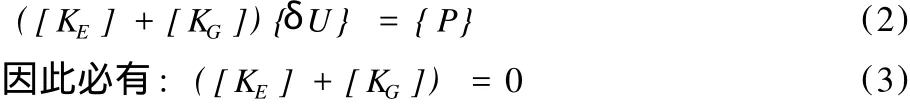
式(3)中的结构弹性刚度矩阵为已知,因外荷载也就是待求的屈曲荷载,故几何刚度矩阵为未知的。为求得该屈曲荷载,任意取一组外荷载{P0},与其对应的几何刚度矩阵为[],并假定屈曲时的荷载为{P0}的λ倍,故有[KG]= λ[K0G],从而式(3)可化为:

式中,λi为第i阶特征值;{φi}为与λi对应的特征向量,是相应该屈曲荷载时结构的变形形状,即屈曲模态或失稳模态。在ANSYS的特征值屈曲分析中,其结果给出的是λi和{φi},即屈曲荷载系数和屈曲模态,而屈曲荷载为λi{P0};只用最小特征值在工程上才有意义,并且将该值作为后续非线性分析的参考荷载因子。

线弹性分析法计算简便,概念清楚,但它的理论基础是分支点稳定理论,只能用于理想结构,不能考虑各种初始缺陷的影响。

(2)非线性稳定分析:考虑结构的初始缺陷、几何非线性和材料非线性,将特征值屈曲模态变形作为结构的初始缺陷加入该结构,修正结构节点坐标后,结合第一类稳定的安全系数将结构外力加大若干倍,采用逐步加载的方式求解结构的极限荷载。

二、工程概况

某大桥为81m下承式钢管混凝土拱桥,桥面系采用纵横梁体系。系梁采用高度为2.0m的实体截面预应力混凝土结构,在主纵梁两端各3.5m范围内需加高至3m。顶宽31.5m,底宽各2.0m,桥面板厚0.3m。梁端设置端横梁,在吊杆处设置中横梁,中横梁中宽度0.3m,中横梁端宽度0.5m。端横梁及中间小横梁均采用矩形截面预应力混凝土结构。本桥共设两榀钢管混凝土拱肋,拱肋的理论计算跨径为77.5m,计算矢高15.5m,矢跨比1/5,拱肋拱轴线采用二次抛物线。拱肋截面为哑铃型,截面高2.5m,上下拱管采用Φ1000x14mm,内灌C50补偿收缩混凝土。上下钢管之间为106cm高腹板,腹板为厚度16mm的钢板。横向两拱肋之间设置3道风撑,风撑采用桁架式,上下弦杆采用Φ200x6mm的空钢管、竖斜杆均采用Φ100x6mm空钢管。拱肋设15对厂制吊杆,吊杆间距顺桥向为4.0m,采用OVM.GJ15-25钢绞线整束挤压拉索。

三、计算模型

(一)有限元模型的建立

本计算模型中拱肋的钢管和混凝土均用梁单元模拟,并分别赋予其材料特性以模拟钢管混凝土的特性。

(1)拱肋上、下弦管为钢管混凝土,模型中采用BEAM188梁单元进行模拟;

(2)横梁、纵梁和风撑均采用BEAM188梁单元模拟;

(3)吊杆和系杆采用L INK10单元模拟,并将单元特性设置为只拉单元;

(4)桥面板采用SHELL181单元模拟。

(二)风撑方案比选

风撑在钢管混凝土拱桥中起着非常重要的作用,风撑的类型将直接影响全桥的稳定性。文中将对此下承式钢管混凝土拱桥在五种风撑类型(三个单片桁式风撑、双片桁式风撑、中间对称K撑、两侧K撑和五个单片桁式风撑)作用下进行弹性稳定分析,并通过比选,选择出最合适风撑形式。在实际工程中只关心结构的第一阶失稳模态,所以只进行第一阶模态的计算。各种类型风撑在各工况下稳定安全系数见表1。

1.施工工况的划分

由于钢管混凝土的主梁施工采用满堂支架方案,所以仅考虑拱圈脱离支架后的最不利施工工况:

(1)拱圈脱离支架,风撑已安装(自重+风载)

(2)顶升上钢管管内混凝土,混凝土未达到强度,仅作荷载(自重+风载)

(3)顶升下钢管管内混凝土,混凝土未达到强度,仅作荷载(自重+风载)

(4)施加二期横载(自重+风载)

(5)使用阶段汽车荷载作用。其中考虑以下几种情况:

①汽车满跨3车道;②汽车满跨6车道

2.各种类型风撑在各工况下稳定安全系数

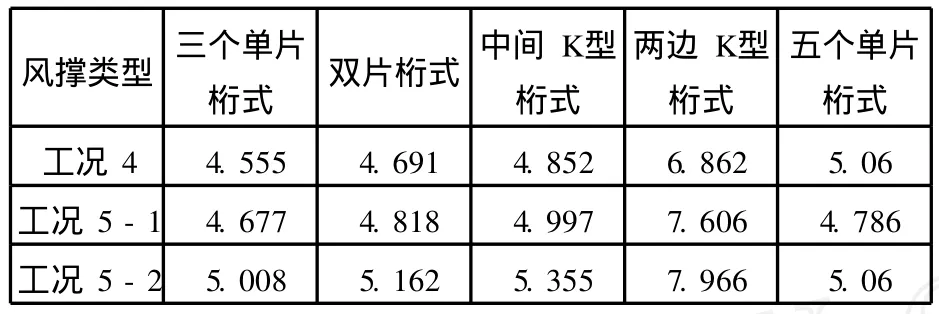
表1 各种类型风撑在各工况下稳定安全系数对比

由表1可明显看出当风撑形式为两边K撑时,稳定系数明显高于其他风撑形式。所以本桥优选两边K撑的方案

该方案有限元模型见图1～2。

图1 有限元模型效果图

图2 有限元模型单元离散图

四、稳定分析

(一)线弹性稳定分析

通过大型有限元软件ANSYS对两边K撑作用下的模型在各工况下进行计算,得到各第一阶屈曲模态如下图所示。

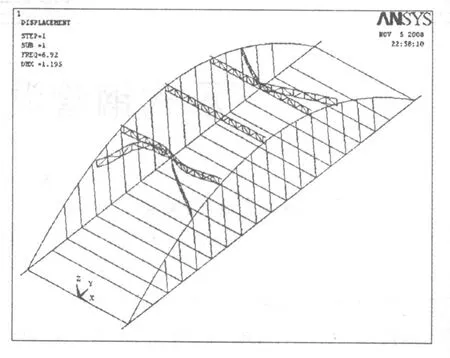
图3 工况1一阶屈曲模态(6.92,风撑面外)

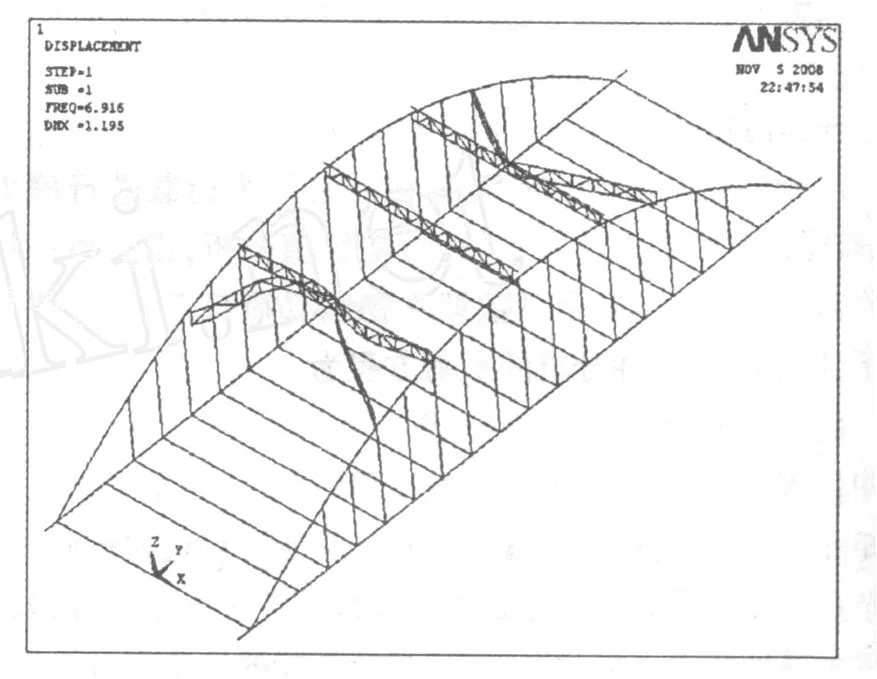
图4 工况2一阶屈曲模态(6.916,风撑面外)

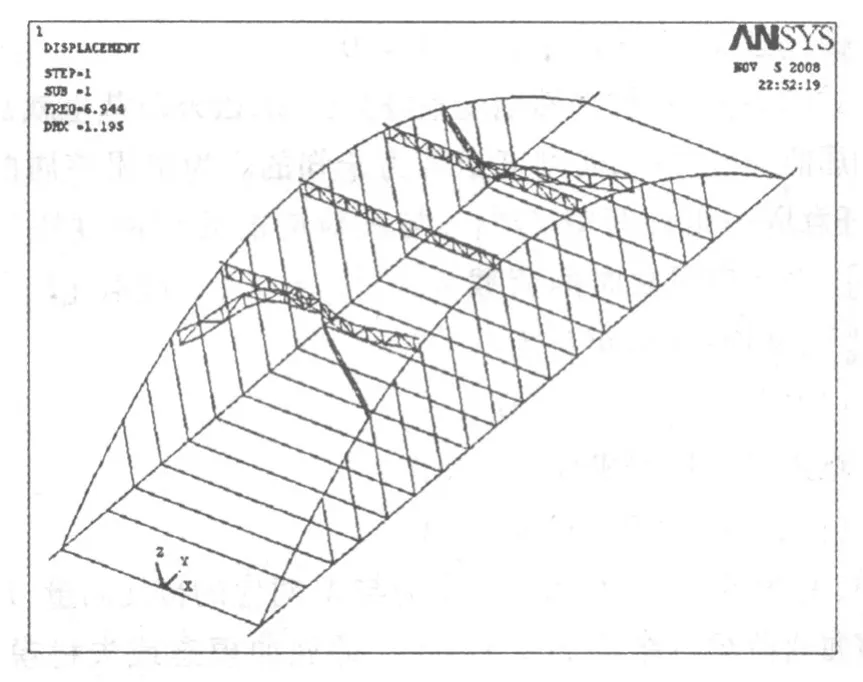
图5 工况3一阶屈曲模态(6.944,风撑面外)

图6 工况4一阶屈曲模态(6.862,拱圈面外)

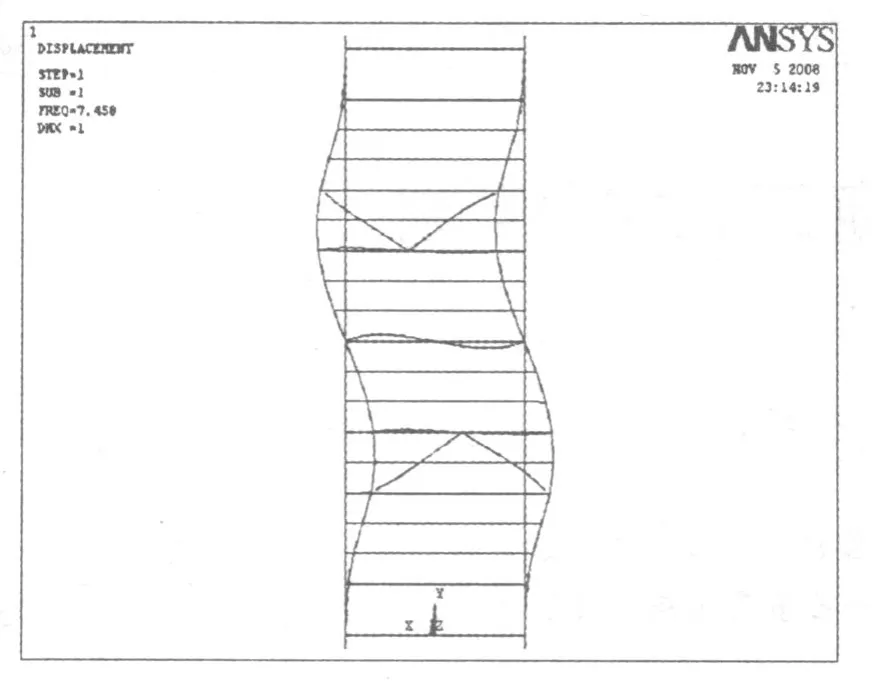
图7 工况5-1一阶屈曲模态(7.606,拱圈面外)

图8 工况5-2一阶屈曲模态(7.966,拱圈面外)

从图中可见,工况1,工况2和工况3第一阶失稳模态均为K撑面外失稳。工况4、工况5-1,工况5-2第一阶失稳模态均为拱圈面外失稳。通过成桥后的失稳模态可以看出该桥的面内刚度相对面外刚度大,说明在运营阶段,面外失稳显得尤为突出。

(二)非线性稳定分析

同时考虑结构的几何非线性和材料非线性,将特征值屈曲模态变形的10%作为结构的初始缺陷加入原结构,修正结构的节点坐标后,将荷载加大若干倍,采用逐步加载的方式求解结构的安全系数。

图9为工况5-2双重非线性分析的K-△曲线,其稳定系数为2.330。

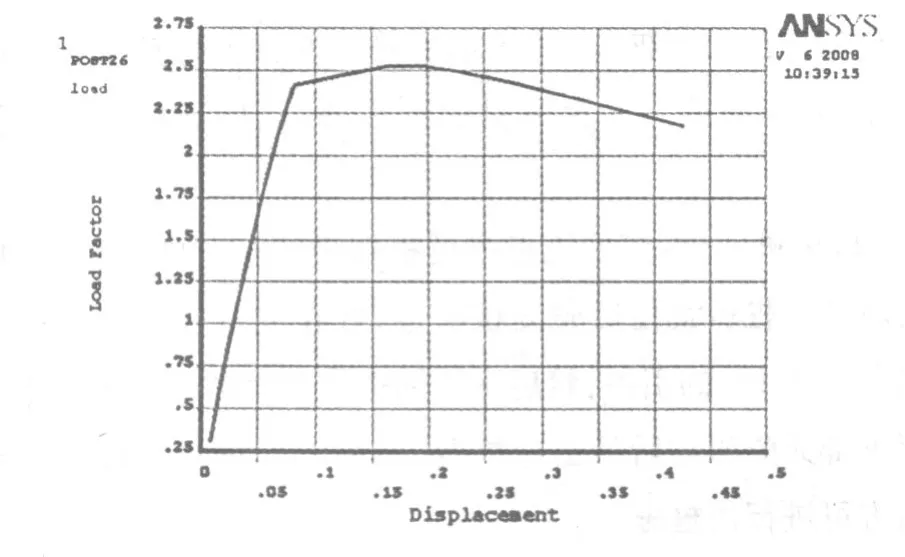
图9 工况5-2双重非线性的K-△曲线

五、计算结果

工况5-2情况下的稳定系数见表2所示。

表2 工况5-2作用下稳定安全系数表

从计算结果可知:

线弹性稳定:通常在实际工程中,结构的第一阶模态的安全系数要求大于4,计算所得稳定安全系数λ均大于4,满足要求。

非线性稳定:考虑几何非线性和材料非线性对结构的稳定影响较大。压溃容许稳定系数一般可计算如下:K>1. 45@ch1.2/0.9=1.93,这里1.45为混凝土材料安全系数,可按混凝土强度标准值/混凝土强度设计值计算,1.2为荷载安全系数,0.9为结构工作条件系数。K=2.33>1.93,可以满足运营阶段的弹塑性稳定要求。

六、结语

(1)通过对各风撑形式作用下稳定安全系数的对比,可知两边K型桁式风撑的稳定明显大于其他形式的风撑,所以采用两边K型桁式风撑,同时为提高风撑的横向刚度,建议适当加大上下弦杆截面由Φ200×6mm加大到Φ219×8mm。

(2)该桥(两边K型桁式风撑)在各工况下的线弹性稳定系数均大于4,满足使用要求。

(3)该桥双重非线性稳定系数与相应线弹性稳定系数的比值为0.293。双重非线性分析考虑了结构初始扰度和材料本构关系,其结果更符合结构受力的实际情况,在该类桥梁设计中应充分重视非线性稳定问题。

[1]公路钢筋混凝土及预应力混凝土桥涵设计规范[S].(JTG D62-2004).北京:人民交通出版社.

[2]陈宝春.钢管混凝土拱桥设计与施工[M].北京:人民交通出版社,1999.

[3]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007.

[4]李国豪,等.桥梁结构稳定与振动[M].北京:中国铁道出版社,1992.

[5]韩林海.钢管混凝土结构[M].北京:科学出版社,2000.

[6]ShamsM,Saadeghvaziri M A.State of the Art of Concrete-Filled steel Tubular Columns[J].ACI Structural Journal,1997,94(5):558 -571.

[7]Schneider S P.Axially Loaded Concrete-filled Steel Tubes,Journal of Structural Engineering[J].ASCE,1998,124(10):1125-1138.

[8]Webb J,Peyton J J.Composite Concrete Filled Steel Tube Columns, Proceedings of the Structural Engineering Conference[M].The Institute of EngineersAustralia,1990.

[9]Ansys Solutions.ANSYS Release 10.0 Documentation[R].2005.

[10]Bathe,K J.Finite Element Proceduces in Engineering Analysis [M].Prentice-Hall Inc,1982.

2010-05-12

吴海军(1981-),男,湖南长沙人,工程师,硕士研究生。