受变动回水影响的洪水位预报研究

王世策

（福建水利电力职业技术学院 永安 366000）

受变动回水影响的洪水位预报研究

王世策

（福建水利电力职业技术学院 永安 366000）

理论上讲，受变动回水的影响的洪水位预报，可以通过受影响河段水面落差反映其影响程度，并加以改正。但实际上，河段的落差无法预报。本文阐述了用水面线计算方法来解决这一问题的途径，经过多年来的作业预报应用，取得了较好的效果。

变动回水 洪水位预报 水面线计算

随着水利水电事业的发展，江河水能资源的开发和梯级水电站的建设方兴未艾，大小河流上水库、拦河坝众多。受水电站变动回水影响的水文站也越来越多，原有的单一关系被破坏，即对同一流量其洪水位因下游电站坝上水位的不同而不同，因此洪水位预报难度增大。

1 变动回水影响的一般概念

洪水位预报断面下游水体水位的变化，产生对预报断面水面比降（落差）的影响，进而引起预报断面水位的变化，使水位流量关系散乱，不成为单一的关系，对同一流量，比降（落差）大水位低，比降（落差）小水位高，下游水体对水位流量关系的这种影响，称为变动回水的影响。产生变动回水的原因一般有：支流测站受干流涨水的顶托；干流测站受下游支流涨水的顶托；下游水库、湖泊、海洋等水体的变化引起的顶托等。

受变动回水影响的水流，一般可认为属于稳定渐变流。因为下游水量的变化一般是缓变的，下游回水顶托引起比降的变化也是缓变的。因此，受变动回水影响时的流量与各水力因素之间的关系可用曼宁公式表示：

式中Q为流量，n为糙率，A为断面面积，R为水力半径，Se为能面比降。在断面稳定，河道顺直时，一般n、A、R均为水位的函数，忽略流速水头的沿程变化，用水面比降S代替能面比降Se，则某水位时因变动回水影响程度不同的

两流量之比为：

用函数关系表示为 Q=g（Z，ΔZ）或 Z=f（Q，ΔZ）。

上式说明了受变动回水影响的水位不仅与上游来水（流量）有关系，还与水面落差有关系。

2 水面线计算方法的应用

受变动回水的影响的洪水位预报，从上述理论上讲，可以通过受影响河段水面落差反映其影响程度，并加以改正。但实际上，河段的落差无法预报。用水面线计算方法成为解决这一问题的一种途径。

2.1 伯努利方程式

天然河道蜿蜒曲折，其过水断面形状和底坡沿程变化，河道糙率沿程变化，流量也是沿程变化的。由于天然河道的上述特点，其水面线常用分段法计算，即采用天然河道非均匀渐变流的伯努利方程式：

式中:Zu、ZL为上、下断面水位；Vu、VL为上、下断面平均流速；hf为沿程水头损失；hξ为局部水头损失；Q为流量；A为断面面积；L为断面间距（河段长度）；n为糙率；R为水力半径；ξ为扩散系数。

山区河流河道断面多呈窄深型，在河流上所建水库库区一般属河川型水库，上述伯努利方程适用于此类库区水面线计算。窄深型河道的断面较为整齐，洪水情况下糙率、扩散系数等参数随水位变化不大，因而在没有足够次数的洪水水面线资料供分析的条件下，同一河段各级洪水位糙率参数采用同一分析成果，基本可行。

2.2 河道糙率计算

在取得可靠的洪水水面线资料、流量资料、河道断面资料的基础上，分析计算河道糙率。将伯努利方程变形，导出河段糙率计算公式，由此计算公式计算出沿江各河段糙率。

2.3 预报流量及坝上起始水位的确定

将上游控制站的实测（或预报）流量合成，并考虑区间入流等因素预报下游站流量。水库管理单位及有关部门，进行水库洪水预报调度，可预计并控制坝上水位过程，根据提供的坝上控制水位，确定水面线计算的坝上起始水位。坝上水位取值误差所带来的水面线计算的误差自下游到上游逐渐减小，对回水末端河段影响最小。

2.4 洪水位计算

采用前述伯努利方程式，根据已有的断面资料、糙率资料，按以上确定的预报流量和坝上起始水位以及库区支流来水量，从坝上断面开始，自下游至上游逐段推算沿河洪水位，预报站断面推算水位即为所求。每一河段水面线计算方法为：河段长度L经量算确定；河段糙率n由历史资料按（3）式计算求得；下断面水位ZL为从坝上断面开始，逐段推算的结果；流量Q由上述预报确定，遇较大支流汇入时，河段流量相应改变；根据上、下断面情况选择扩散系数ξ：逐渐扩散ξ=0.3～0.5，急剧扩散ξ=0.5～1.0，收缩河段局部水头损失可以忽略，ξ=0。假定上断面水位Zu,可计算出方程式两边的数值,若方程两边的数值相等或接近，则假定的Zu即为所求，否则，应重新假定Zu，重新计算，直至求出Zu为止。

表1 河段糙率计算表

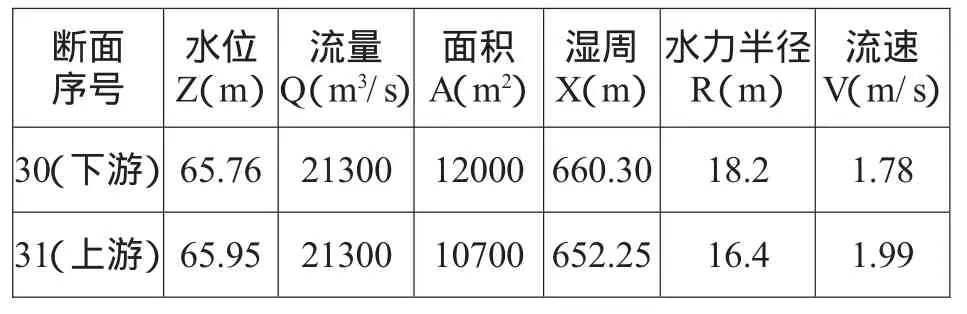
表2 河段水面线计算数据表

3 应用实例

3.1 洪水位计算

现以某库区一场洪水为例，说明其作业预报过程。1999年5月26日20时，预报5月27日5时预报站流量21300 m3/s，预计库区区间主要支流相应入库流量1200 m3/s，根据该水库洪水预报调度，预计5月27日5时坝上水位60.9m，按照上述方法，计算沿江各断面洪水位，直至预报站断面。由于河段数甚多，仅列举一个河段（30～31号断面）进行洪水水面线计算，进一步说明方程中各参数的确定。

3.1.1 30号断面至31号断面河段长L=1880m。

3.1.2 河段糙率根据往年同期洪水资料按（3）式计算而得，该河段糙率计算的有关数据见表1。从上表数据可以看出，该河段属逐渐扩散河段，ξ取0.3，将以上数据代入河段糙率计算公式求得n=0.038。

3.1.3 下断面水位ZL=65.76m（从下游向上游逐段推算结果）。

3.1.4 流量Q=21300 m3/s（预报断面至此河段无大支流加入，直接采用预报断面流量）。

3.1.5 扩散系数ξ取0.3。

假定上游水位Zu，将以上参数代入（2）式，逐次逼近试算，当Zu=65.95m时，方程两边数值为66.15，Zu=65.95m即为所求。该河段有关水面线计算数据见表2。

按上述方法逐段计算至预报站断面，得预报站断面洪峰水位为71.15m，实测洪峰水位为71.27m，误差为-0.12m。

3.2 洪水位作业预报精度评定

本预报方法在近年洪水位预报中应用的效果较好。根据《水文情报预报规范》作业预报精度评定方法，预报合格率达82%。

4 结语

水面线计算方法对于受变动回水影响的洪水位预报是一种行之有效的途径，还可预报出沿江沿河各地的洪水位，为防汛服务。但该法对基础资料要求高，计算量大，必须投入大量的人力、物力收集准确可靠的基础资料，并经过大量的数学计算，分析沿河水力参数和进行作业预报。将其编制成计算机软件，用计算机计算，十分方便快捷，如能结合水库洪水预报调度系统使用，则效果更佳

（专栏编辑：张 婷）