立管涡激振动的离散涡数值模拟

陈 伟, 宗 智

(1.大连理工大学,大连 116023;2.工业装备结构分析国家重点实验室,大连 116023)

立管涡激振动的离散涡数值模拟

陈 伟1,2, 宗 智1,2

(1.大连理工大学,大连 116023;2.工业装备结构分析国家重点实验室,大连 116023)

通过离散涡方法求解立管所受涡激升力,并与立管动力响应方程相耦合来对涡激振动问题进行时域内的数值模拟。通过在均匀来流和剪切来流下的模拟,所得的结论与其他文献中的结论比较吻合,较好地揭示了立管涡激振动的特征。

立管;涡激振动;离散涡方法;CFD

Abstract:Discrete vortex method is used to calculate the lifting force induced by the vortex shedding from the structure.The results will couple with the riser dynamic response equation to realize a numerical simulation of VIV in time domain.Some conclusions are got after simulating the VIV phenomenon of riser under uniform flow and shear flow,then they compared with other literatures’conclusions show a good agreement,and the VIV characteristics of riser are revealed better.

Key words:riser;Votex-Induced Vibration;discrete vortex method;CFD

0 引言

立管是海洋结构物不可或缺但又十分薄弱的子系统。在海洋洋流环境下,立管结构由于发生泄涡而产生的涡激振动会缩短结构的疲劳寿命,甚至会引起结构的破坏。涡激振动问题是流体力学中复杂的问题之一,一直困扰着学术、工程界[1]。对立管的涡激振动研究可分为实验和数值模拟等两方面研究。前者主要集中在模型试验,现场实验因花费巨大而很少进行;后者因借助于计算能力的飞速发展而多有进行。但目前全三维的数值模拟仍不可行。关于涡激振动的诸多计算方法,可见文献[2]。

本文采用离散涡方法(DVM)求解 N-S方程,DVM方法将速度与压力表示的控制方程转变为涡量场来求解,减小了计算区域,具有不依赖于计算网格等优点,较适合高雷诺数条件下的流场计算[3]。离散涡方法至今在提高精度和计算效率方面已有很大的改进,在工程领域得以广泛应用[4]。

立管结构尺度比很大,对其进行三维数值模拟目前还不现实。本文借助船舶水动力计算的切片思路,沿立管长度方向取若干个水动力剖面,在这些剖面上进行二维流场求解,同时与立管的动力响应方程相互耦合来实现立管结构的涡激振动模拟。

1 离散涡方法介绍

以涡量ω和流函数ψ表示的二维不可压缩非定常粘性流动的控制方程为

式中v为流体的运动粘性系数。离散涡方法将连续的涡量场离散,把离散的涡元视为粒子,在拉格朗日框架内离散求解上述控制方程。

Chorin提出算子分裂法[5]来处理考虑粘性时的(1)式,将其分为对流和粘性扩散2个部分:

对流部分:

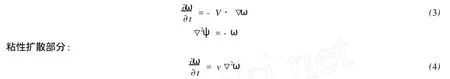
对于(3)式的求解即为不考虑粘性时涡元粒子之间的相互诱导,而(4)式的解与随机运动过程的解相同,可以采用随机走位法来求解。离散涡方法主要分为物面涡的生成、涡元的对流和扩散、涡元的消除和融合、物体受力计算等几个方面,其具体列式和步骤可参考文献[6,7]。

2 立管模型

考虑轴向变形时立管的控制方程可写为[8]

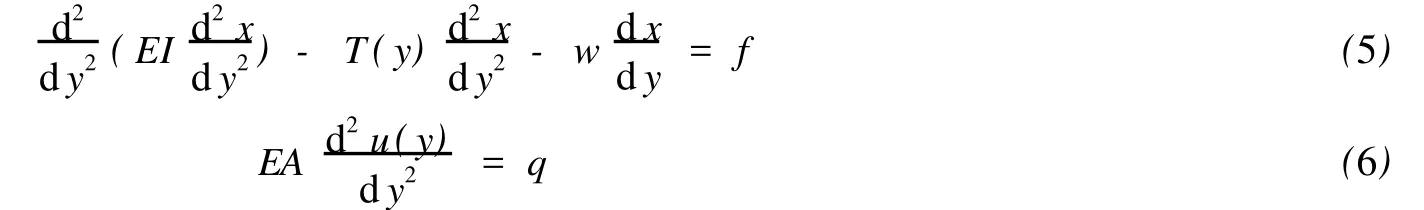
式(5)中:EI是立管的弯曲刚度;T是作用在管壁的轴向张力;w是单位长度立管的重量(包括内部液体);f是单位长度的横向载荷。取y轴垂直向上,x为水平方向,坐标原点在海底。式(6)中:A为立管的实体截面面积;u为轴向位移;q为轴向载荷。采用迦辽金法对上两式处理可得到立管弹性刚度矩阵 KE和几何刚度矩阵KG。由此可求得一定来流下立管的静平衡位置:

式中:d为广义位移向量;F为载荷向量。本文采用直接迭代法求得立管的静平衡位置,此处所得到的总刚度矩阵在动力求解过程中保持不变。立管的阻尼采用瑞利阻尼,振型阻尼取5%。动力响应方程为

式中:M、B、K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵;F(t)为外载荷矩阵。本文模型采用的是杆梁的组合模型。所选取的立管和海水参数如表1所示,立管为 TTR型,两端简支处理。

表1 立管和海水的相关参数[9,10]

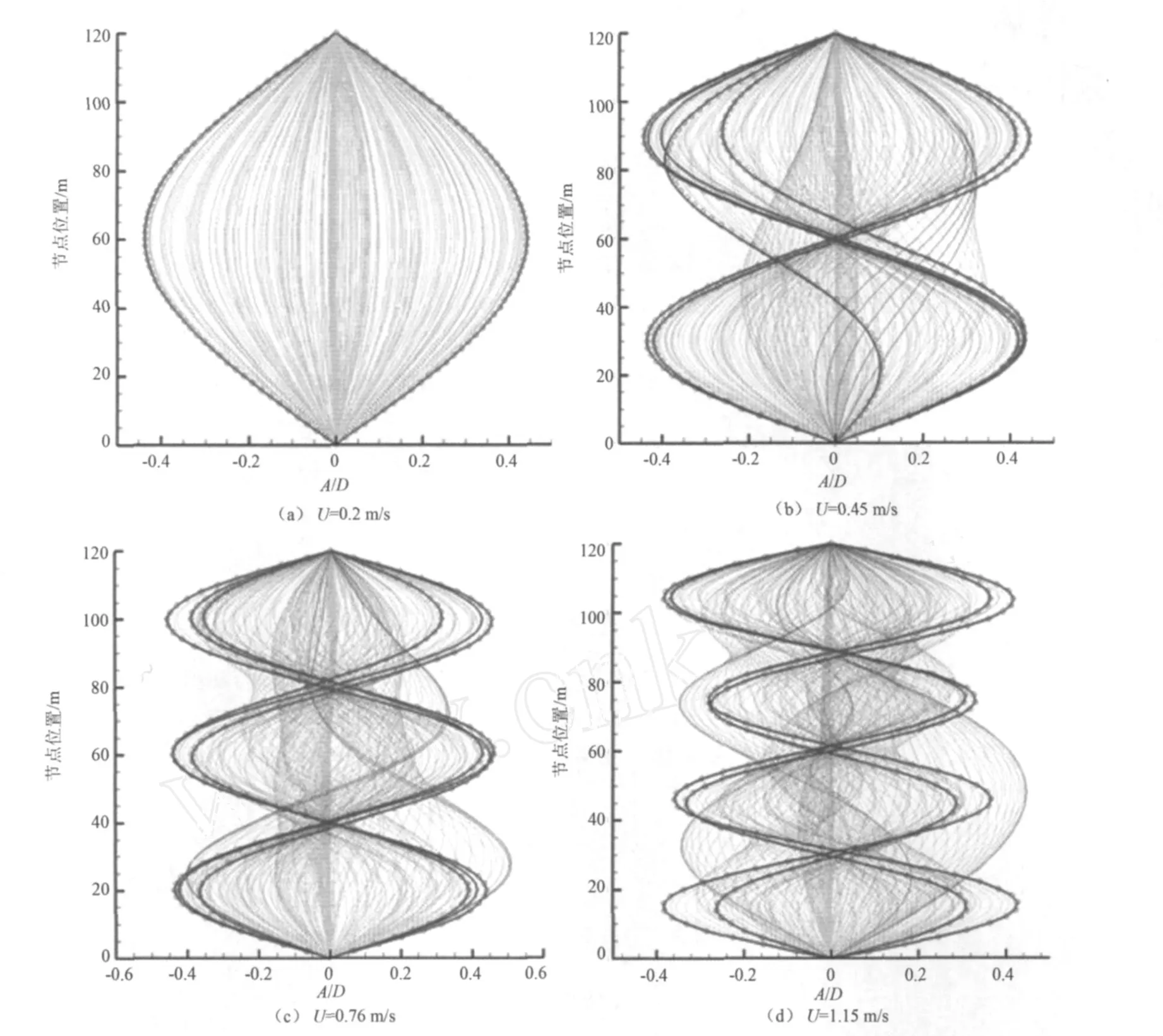
图1 不同来流速度下的横向振动位移

3 数值模拟流程

为简化计算模型,在动力求解中假定结构刚度矩阵保持不变,立管在一定来流下的静平衡位置附近振动。因此,首先计算得到立管的静平衡位置。为后文分析方便还需要对立管进行模态求解。进入动力求解后,在同一时刻,对所有的水动力剖面,即集中质量所在位置进行DVM求解,得到结构的外载荷矩阵;然后用Newmark方法求解结构在下一时刻的动力响应,得到各节点处的运动物理量和新位置后,再利用DVM求外载荷。几经如此反复后,实现流固耦合模拟。

4 数值模拟结果

实际环境下的海流沿垂向分布形式往往较复杂,本文采用FORTRAN编程计算了均匀来流和剪切来流情况下的立管涡激响应。立管沿长度方向划分为60个长度相同的单元,需要计算的流体剖面有50个,各水动力剖面每次新生120个点涡。采用TECPLOT软件示意计算结果。

4.1 均匀来流下立管的涡激振动

在均匀来流情况下,所取来流速度大小范围为0.16 m/s～1.5 m/s,其对应的雷诺数范围为4.0×104～3.75×105,此时的斯托哈尔数在0.21左右。来流速度分别为0.2、0.45、0.76和1.15 m/s时立管的横向振动位移如图1所示。图中粗实线是出现最大节点位移时的主振型,细实线描述了出现最大节点位移时的次要振型,而细虚线则表示其他时刻的振型。由图1可知,随着来流速度的增加,立管振动的模态也随之增加。对于同一立管模型,文献[10]中取80个单元,计算出各模态下的最大振幅在0.6左右,本文为0.42,误差的原因还需进一步分析。

图2所示在上述四个来流速度下,计算500个时间步长后立管各水动力剖面内的尾流涡元分布。对比尾流涡元分布图及其相应的振动位移响应图可知,尾流的涡形式沿立管长度方向发生变化:在振动剧烈的部位,尾涡呈现出2P模式;在振动的“节点”处,尾流为2S模式。这与 Techet等人进行的试验[10]结果一致。各来流下的涡模式变化都已在图中标出。对于上述四个来流速度,取 Z=24 m这一水动力剖面,其位移和升力时程曲线如图3所示。

根据折合速度Ur的定义,其倒数称为折合频率,即

在均匀来流情况下,fn取振动的模态频率;U为来流速度;D为圆柱直径。表2列出了各个来流速度下计算的时间步长、主要的响应模态、对应的折合速度以及折合频率。

由表2可见,立管的涡激振动的折合速度大都保持在4～7之间,即在这一区间内立管从外界流体获取能量,对应的折合频率为0.25～0.14,正好包含斯托哈尔数 St所在的区间。由于 St表示的是泄涡频率特征,这说明涡激振动中泄涡频率有较宽的频带,不同来流下锁定发生的频率亦有不同。所有这些都表明立管的振动模态是由泄涡和锁定发生的区间来控制的。

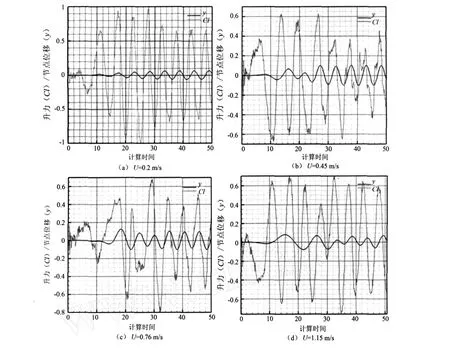
图3 不同速度下的振动位移和升力系数时程曲线,y=24 m

4.2 剪切来流下立管的涡激振动

本文考虑梯形和三角形两种形式下的剪切来流,最大来流速度取1.2 m/s,最小速度取0.4 m/s。计算所得的立管振动响应如图4所示。可见,在剪切来流情况下,立管的振动位移较均匀来流情况下要小很多,这是由于沿立管长度方向雷诺数与泄涡频率不同所造成的。但主要的振动频率还是由平均雷诺数下的泄涡所控制。此时的平均来流为0.8 m/s,参考表2可知,正是第三阶频率占主要地位,这与模拟结果一致。

表2 不同来流速度下立管响应特性

5 结论

通过对立管在均匀来流和剪切来流下的涡激振动数值模拟,得到如下结论:

(1)在均匀来流情况下,随着来流速度的增加,立管振动的模态会随之增加。立管最大的位移并不一定发生在主要模态上。尾涡的形式沿立管长度方向发生变化,在振动剧烈的区域为2P模式,振动的“节点”区域为2S模式。(2)剪切来流情况下由于沿立管长度方向泄涡频率各不一样,导致立管的振动位移比均匀来流情况下的要小。泄涡频率不同,导致立管受激发获取能量的区域同样比均匀来流情况下的要小。(3)立管的振动模态是由泄涡频率和锁定的区间所控制的。

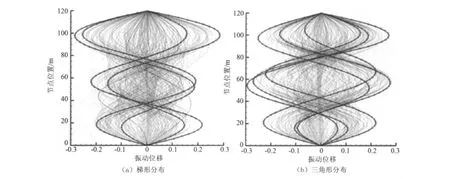
图4 剪切流下立管的振动位移

[1] 潘志远.海洋立管涡激振动机理与预报方法研究[D].上海:上海交通大学,2006.

[2] 秦延龙,王世澎.海洋立管涡激振动计算方法进展[J].中国海洋平台,2008,23(4):14-17.

[3] 祝宝山.非定常流动的快速拉格朗日涡方法数值模拟[J].力学学报,2008,40(1):9-18.

[4] Kamemoto K.On contribution of advanced vortex element methods toward virtual reality of unsteady vortical flows in the new generation of CFD[J].ABCM,2004,XXVI(4):368-378.

[5] Chorin A J.Numerical study of slightly viscous flow[J].Journal of Fluid Mechanics,1973,57:785-796.

[6] Mustto A A,Bodstein G C R.Improved vortex method for the simulation of the flow around circular cylinders[C].AIAA,2001,NO:A01-31110,pp:1-11.

[7] 潘岩松.高层建筑二维流场的离散涡方法数值模拟[D].武汉:华中科技大学,2004.

[8] Patel M H,Witz J A.Complaint Offshore structures[M].Butterworth-Heinemann,England,1991.

[9] Silvio B C Martins,Sergio H Sphaier,Severino F Silva Neto.Integrated fluid-structure model(RVM-FEM)for riser analysis[C].International Offshore and Polar Engineering Conference,2004,2:105-112.

[10] Yamamoto C T,Meneghini J R,Saltara F,Fregonesi R A,Ferrari J A Jr.Numerical simulation of vortex-induced vibration on flexible cylinders[J].Journal of Fluids and Structures,2004,19:467-489.

Numerical Simulation of Vortex-Induced Vibration for Risers by Discrete Vortex Method

CHEN Wei1,2, ZONG Zhi1,2
(1.Dalian University of Technology,Dalian 116023,China;2.State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian 116023,China)

O327,P751

A

1001-4500(2010)01-0026-06

2009-08-19; 修改稿收到日期:2009-10-30

陈 伟(1985-),男,硕士研究生,从事船舶与海洋结构物设计与制造工作。