涉及单形旁切球半径的两类几何不等式

张晗方

(徐州师范大学 数学科学学院, 江苏 徐州 221116 )

涉及单形旁切球半径的两类几何不等式

张晗方

(徐州师范大学 数学科学学院, 江苏 徐州 221116 )

利用分析的方法给出了n维欧氏空间En中涉及单形旁切球半径的两类几何不等式, 由此得到了n维欧氏空间En中涉及单形旁切球半径的一系列几何不等式, 给出了一系列特例.

单形; 旁切球; 内切球; 半径; 高; 不等式

Abstract:Two algebraic inequalities are presented in this paper. Based on it, we know that a class of geometric inequalities of involves radius of escribed sphere in n dimensional Euclidean space En. And some corollaries are given.

Key words:simplex; escribed sphere; inscribed sphere; radius; altitude; inequality

引言

设ΔABC的三边a, b, c对应的高分别是ha, hb, hc, 对应的旁切球半径依次为ra, rb, rc. 据文[1]介绍, 1965年, C. Cosnita和F. Turtolu建立了下面有关ΔABC的高和旁切圆半径的不等式

等式成立当且仅当ΔABC为正三角形.

又若设r为ΔABC的内切圆的半径, 则有

等式成立当且仅当ΔABC为正三角形.

实际上, 在顶点集为{A1, A2, A3, A4}的四面体Ω中, 若设r为四面体Ω的内切球半径, ri为顶点Ai(1≤i ≤4)所对的界面的旁切球半径, 则不难证明

等式成立当且仅当Ω为正四面体.

同样, 若再设hi为四面体Ω的顶点Ai(1≤i≤4)所对的界面上的高, 我们也可以证明

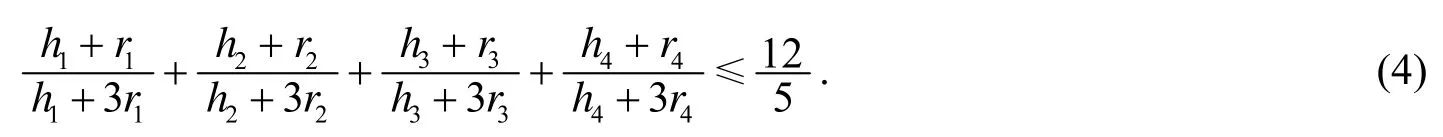
等式成立当且仅当Ω为正四面体.

对于Cosnita-Turtolu不等式(1), 作者在文[2]中将其推广到了n 维欧氏空间En中的单形的情形, 并且还作了指数以及系数的推广.

那么对于(3)与(4)来说, 能否将其推广到n 维欧氏空间En中去呢？回答是肯定的. 关于涉及单形的旁切球半径问题, 在文[3]、[4]中也作了进一步地讨论.

1 两个引理

为了将上述的(3)与(4)推广到n维欧氏空间nE中去, 我们首先给出两个引理.

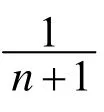
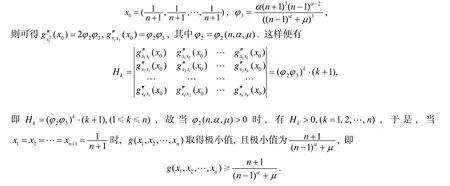
2 主要结果及其证明

定理1 设Ω为n维欧氏空间En中的单形, 其顶点集为A={A1,A2,…,An+1}, r为Ω的内切球半径, ri为顶点Ai所对的n-1维界面的旁切球半径, 正实数α与μ满足引理1中的条件, 则对于实数λ, 当λ+μ＞0时, 有

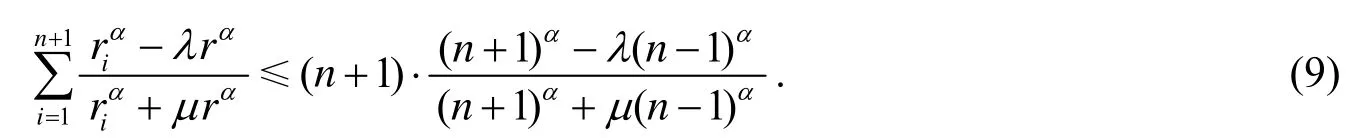
等式成立当且仅当Ω为正则单形.

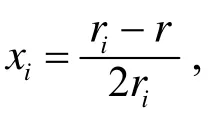
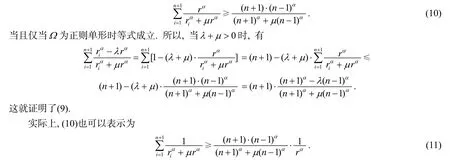
等式成立当且仅当Ω为正则单形.

由R≥nr, 利用(11)立即可得如下的推论.

推论1在定理1的条件下, 设R为单形 的外接球半径, 则有

定理2 设Ω为n维欧式空间En中的单形, 其顶点集为A={A1, A2,…,An+1}, hi为顶点Ai所对的

n-1维界面上的高, ri为顶点Ai所对的n-1维界面的旁切球半径, 正实数α与μ满足引理2中的条件,对于实数λ, 当λ＜μ时, 有

此即为(18), 当α≠1且μ≠2时, 等式成立当且仅当Ω为正则单形.

推论5在定理2的条件下, 当λ＞μ时, 有

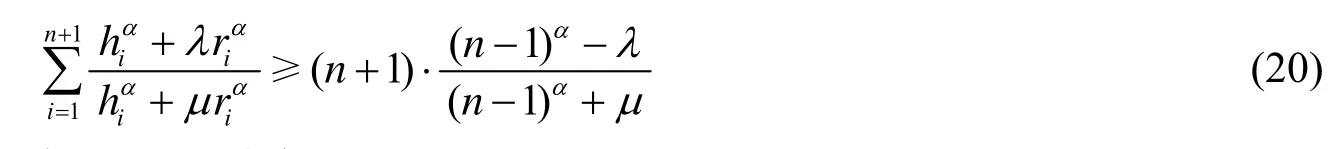
在α≠1且μ≠2时, 等式成立当且仅当Ω为正则单形.

实际上, 由定理2的证明过程容易看出, 当λ＞μ时, 立即可得(20).

由(18)知, 若记

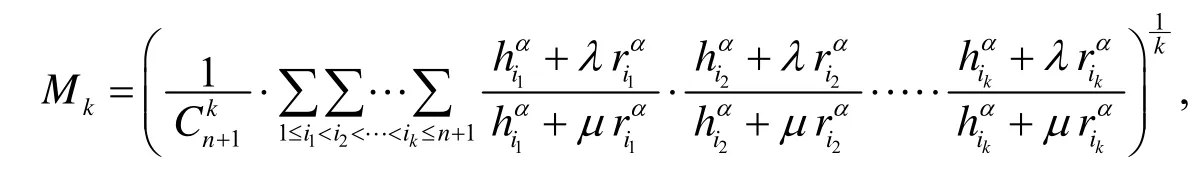
则由Maclaurin不等式[4,5,6]可得如下的

推论6 在定理2的条件下, 有

定理5矩阵环Pn×n至多有n+1个互不同构的左理想.

证明设Ω是Pn×n的任一左理想, 且r=max{rankX| X∈Ω}. 由引理4 知, 存在一个可逆矩阵T∈Pn×n, 使得 ΩT=〈E11,E22,…,Err〉. 注意T-1ΩT=ΩT , 直接验证可知,

是左理想Ω到ΩT的一个同构映射. 因此Pn×n的任一左理想与下面的左理想之一同构:

这表明Pn×n至多有n+1个互不同构的左理想.

推论6矩阵环Pn×n至多有n+1个互不同构的右理想.

证明注意Ω是Pn×n右理想当且仅当ΩT={AT|A ∈Ω}是Pn×n的左理想. 于是从定理5 可得所需的结论.

[1] 张禾瑞, 郝鈵新. 高等代数(第四版) [M]. 北京: 高等教育出版社, 1999

[2] 北京大学数学系几何与代数教研室前代数小组. 高等代数[M]. 第三版. 北京: 高等教育出版社, 2003

[3] 张禾瑞. 近世代数基础[M]. 北京: 高等教育出版社, 1978

[4] 熊全淹. 近世代数[M]. 武昌: 武汉大学出版社, 1991

[5] 杨子胥. 近世代数(第三版) [M]. 北京: 高等教育出版社, 2003

[6] 徐诚浩. 抽象代数——方法导引[M]. 上海: 复旦大学出版社, 1989

[7] 杨子胥, 宋宝和. 近世代数习题解[M]. 济南: 山东科学技术出版社, 2003

[8] 左连翠. 矩阵环中的单侧理想及伪理想[J]. 济南大学学报, 1999, 9(2): 19～21

Two Geometric Inequalities of Involving Radius of Escribed Sphere of Simplex

ZHANG Han-fang
(School of Mathematics Science, Xuzhou Normal University, Xuzhou 221116, China)

A

1672-5298(2010)01-0006-05

2009-11-22

张晗方(1955- ), 男, 江苏东海人, 徐州师范大学数学科学学院教授. 主要研究方向: 距离几何、不等式