Cu3N 弹性和热力学性质的第一性原理研究*

李世娜刘永

(燕山大学理学院，秦皇岛066004)

(2010年1月11日收到;2010年1月30日收到修改稿)

Cu3N 弹性和热力学性质的第一性原理研究*

李世娜†刘永

(燕山大学理学院，秦皇岛066004)

(2010年1月11日收到;2010年1月30日收到修改稿)

利用基于密度泛函理论的第一性原理全势线性缀加平面波方法，研究了立方反ReO3结构Cu3N在零温(0K)零压下的平衡晶格常数、体弹模量及其对压强的一阶导数，计算结果与其他实验及理论结果基本相符.同时得出Cu3N的弹性常数，Poisson比等，并分析出Cu3N在零温零压下是稳定的.通过准谐Debye模型计算Cu3N的热力学性质，得到了Cu3N的晶格常数、等压比热容、等容比热容、热胀系数与温度和压强之间的关系，同时计算出不同温度不同压强下其体弹模量及Debye温度的值.

热力学性质，弹性常数，第一性原理，Cu3N

PACC:0570C，6220D，7115A

1. 引言

过渡金属氮化物由于在磁学、光学和形态学等方面的极好性质及在电子器件等领域的应用引起了人们的广泛兴趣，如化合物BN，AlN等，但共价氮化铜(Cu3N)为人们所不熟悉.Cu3N是一种以共价键结合的金属氮化物.块体的Cu3N晶体密度为5.84 g/cm3，分子量为204.63，颜色呈黑绿色或红褐色.无毒廉价材料Cu3N具有较高的电阻率，较低的热分解温度和独特的光电特性在光存储器件和高速集成电路应用方面备受关注［1，2］.此外，Cu3N还是应用于低磁阻隧道结的阻挡层的候选材料［3］.

在3d过渡金属(Ti，Cr，Fe，Co，Ni，Cu)的氮化物中，随着原子序数的增大，与N2气反应活性依次降低，Cu的反应活性最低.起初Cu3N只能通过Cu2O和NH3作为初始材料通过复分解反应制备得到［4］.近年来人们使用多种制备技术获得Cu3N薄膜，如直流反应溅射法［5］、射频磁控溅射发［6］、分子束外延法［7］、脉冲激光反应沉淀法［8］等.Cu3N薄膜的生长条件对它的结构性质等有一定的影响.国际上报道的有关Cu3N的物理及化学性质并不一致: Cu3N有时候表现出低反射率高阻抗的半导体性质，有时候表现出金属性质［8，9］;Maruyama和Marushita指出Cu3N薄膜晶格常数a>3.868(1=10－10m)为导体，小于3.868为绝缘体［3］;热分解温度在100—400℃之间［7，10，11］等.因此对Cu3N开展研究非常有必要.

Cu3N是立方反ReO3结构，空间点群是Pm-3m，一个晶胞中Cu原子占据各立方边边线的中心位置而N原子占据立方晶胞的8个顶点，此结构的体心位置有一较大间隙，Cu原子以及其他原子如Pd、碱金属原子等很有可能进入此位置导致Cu3N的电学性能、光学性能等发生很大的变化［2，12］.Yu等［13，14］得出Cu3N的带隙随压强的增大而减小.在高压下反ReO3结构的Cu3N由半导体向金属相转变.这使得该材料具有很大的潜在应用价值.但是运用全势线性缀加平面波法计算弹性常数，以及结合Debye模型计算Cu3N的热力学性质还没有具体的报道.

本文利用全势线性缀加平面波方法研究了块状反ReO3结构Cu3N的基本性质参数，获得了Cu3N的平衡晶格常数a，体弹模量及其对压强的一阶导数、弹性常数.另外，通过准谐Debye模型计算了Cu3N在压强0—5 GPa，温度0—700K范围内的Debye温度、热容量、热胀系数α等热力学性质.

2. 模拟方法

本文采用基于第一性原理的密度泛函理论［15］全势线性缀加平面波法［16］进行计算，使用广义梯度近似处理交换相关势能(WIEN2K软件包［17］).对Kohn-Sham方程和能量泛函进行了自洽求解，可以得到所求电子体系的基态密度、总能和能量本征值.在缀加平面波方法中，空间被分割为间隙区(intertitial region，简记为IR)和以原子位置为中心的非重叠糕模球(muffin-tin，简记为MT).每个MT球内波函数球谐基矢的角动量截断取为lmax=10.波函数的平面波截断由RMT*Kmax=8决定，其中RMT是晶胞中最小的MT半径，Kmax是平面波展开中最大的倒格子矢量.在电荷密度Fourier展开中Gmax=14.Cu和N的MT半径分别取为1.8 a.u.，1.6 a.u..自洽循环计算的收敛标准为0.0001电荷电量.

为了研究Cu3N的热力学性质，使用了准谐Debye模型［18，19］.在此模型中，Cu3N的非平衡Gibbs函数G*(V;P，T)形式如下:

在(1)式的右边，E(V)表示每个原胞的总能量，P，V和T分别表示压强、体积和温度，Avib是振动的Helmholtz自由能，其中Θ(V)是Debye温度.考虑到准谐近似并使用声子态密度的Debye模型，Avib可表示为［20，21］

D(Θ/T)是Debye积分，n是每个原胞中包含的原子数，kB是Boltzmann常数.对于各项同性的固体来说，Θ可表达为［21］

M是每个原胞中分子的质量，Bs是用来表示晶体压缩率的绝热体积模量，σ是Poisson比，可以表达为［20］

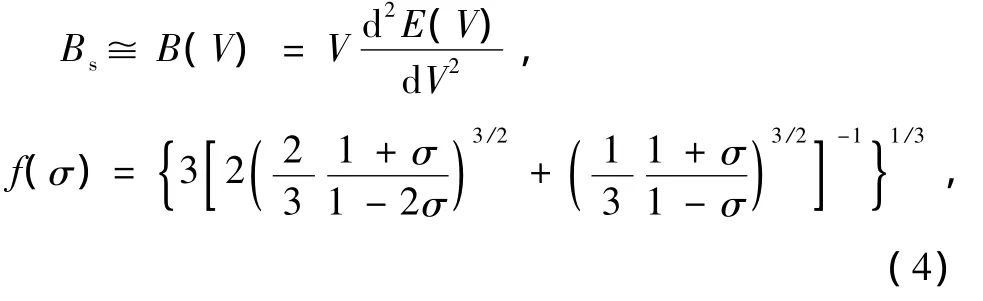
非平衡Gibbs函数G*(V;P，T)对体积求最小值，即

通过(5)式可以得到热状态方程(EOS)，

其中振动内能Uvib和Grüneisen参数γ表达式分别为［21］

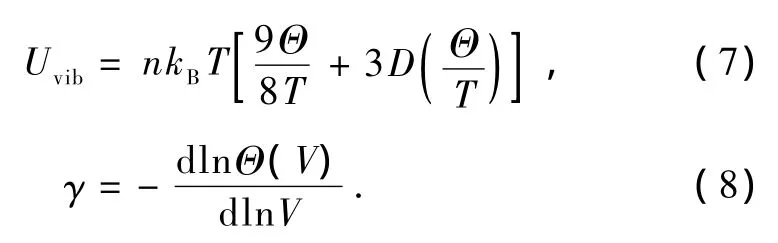
等温体弹模量BT，等容热容CV，等压热容CP和热膨胀系数α分别表示为［18］

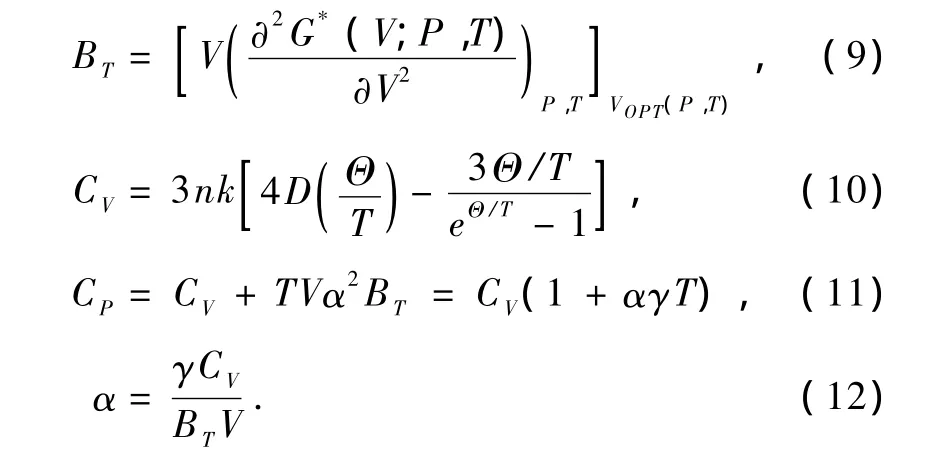
3. 结果与讨论

3.1. Cu3N基本的性质参数

为了确定立方反ReO3结构Cu3N的体结构性质，我们采用Murnaghan状态方程进行拟合［22］，计算了晶体体积与系统总能之间的关系.图1为本文研究的Cu3N的结构图，浅色小球表示N原子，黑色大球表示Cu原子.图2为总能量E和原胞体积V的关系，本文计算出的能量为图中纵轴所示能量减去136596 eV.由图2知，Cu3N在零温零压下，V=56.32013是最稳定.由此，可求出零温零压下的晶格常数a0=3.833，体弹模量B0及其对压强的一阶导数B′0，如表1所示.所得结果与其他理论计算结果和实验结果相符合.

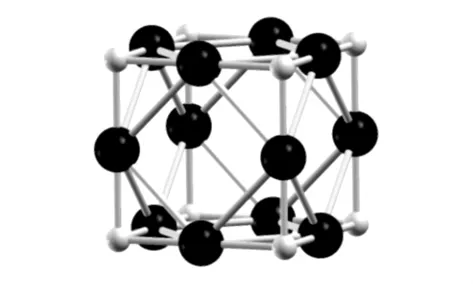
图1 Cu3N结构图

图2 能量与体积关系图

表1 在零温零压下Cu3N的晶格常数、体积模量及其对压强的一阶导数

3.2. 弹性常数

弹性性质跟晶体的比热容、Debye温度和热容等性质密切相关.在研究立方反ReO3结构的Cu3N的弹性常数时，能获得其结构稳定性等方面的信息.立方晶格Cu3N体系中包含3个独立的弹性系数C11，C12和C44.如图3弹性常数Cij通过以下3种变形方式得到:1)与结构优化相似的均匀体积膨胀和收缩的变形(EOS，如图3(a)所示);2)沿［111］体对角线的菱方(rhomb)变形如图3(b)所示;3)保持体积恒定沿［001］方向的四方(tetra)变形如图3(c)所示.其中本文计算出的能量为图中纵轴所示能量减去136596 eV.弹性常数通过体积模数B，剪切模量G，杨氏模量E和Poisson比σ来决定晶体对外力的响应［24］.

立方晶格的体弹模量与弹性常数Cij之间的关系为［25］:B=1/3(C11+C12).根据Voigt近似，剪切模量GV跟晶体弹性常数Cij有如下关系:GV=(C11－C12+3C44)/5.然而根据Reuss近似，又可得剪切模量GR跟晶体弹性常数Cij之间有如下关系:GR=5 (C11﹣C12)C44/［4C44+3(C11－C12)］.Hill证明，Voigt和Reuss的方程描述的分别是晶体剪切模量的上限和下限，给出晶体的剪切模量:G=1/2(GV+ GR).杨氏模量E，剪切模量G及体弹模量B之间的关系式为:E=9GB/(3B+G).

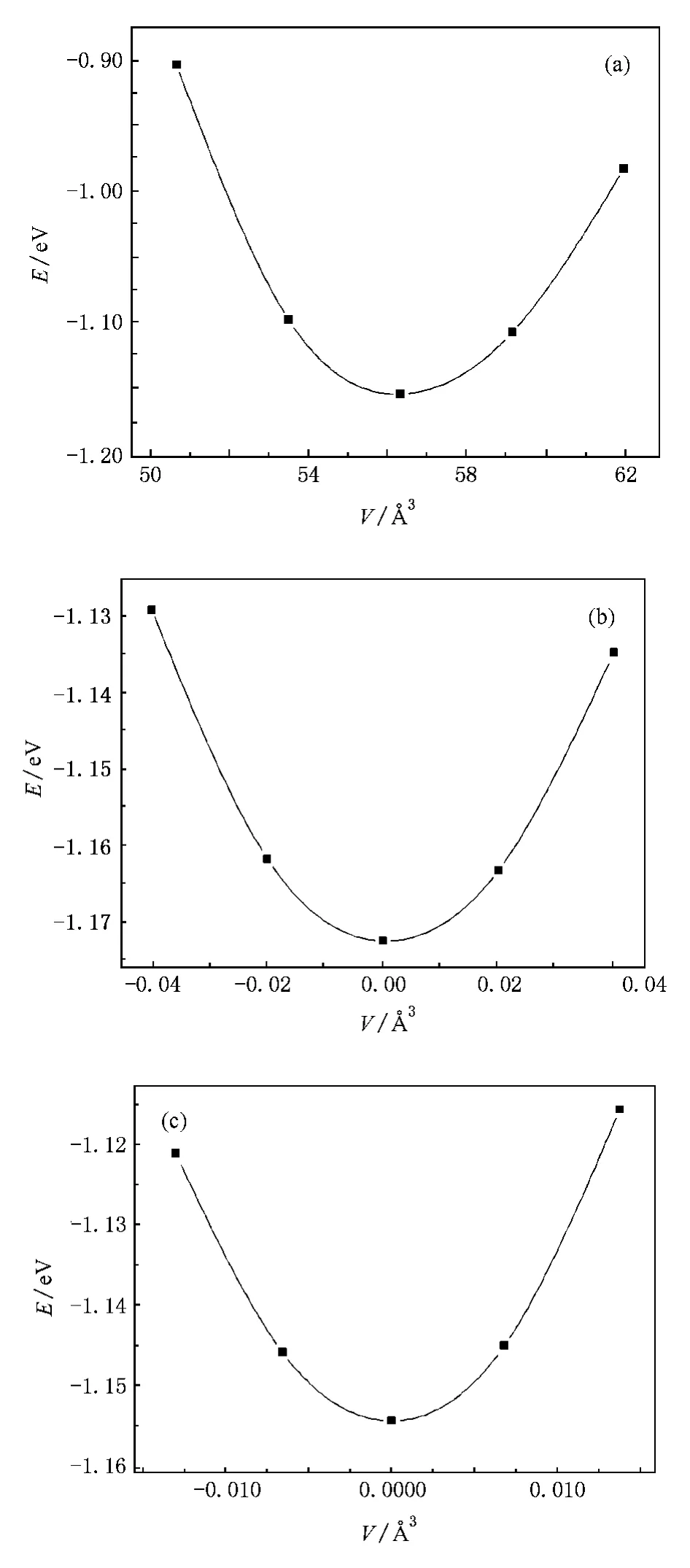
图3 Cu3N三种弹性应变曲线(a)体积膨胀与压缩的变形，(b)菱方变形，(c)四方变形

计算出的Cu3N的弹性常数Cij，剪切模量G等参数如表2所示.本文得到的Poisson比为σ=(3B－E)/6B=0.358102.由表2，Cu3N满足以下条件［24］:

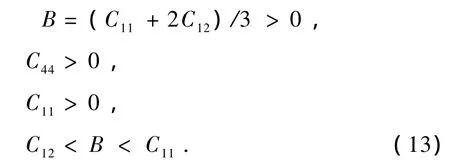
立方反ReO3结构的Cu3N在零温零压平衡条件下是稳定的.

表2 Cu3N的弹性常数a及各弹性模数值(单位:GPa)

3.3. 热力学性质

本文有效地利用准谐Debye模型，计算了T在0—700K，P在0—5 GPa范围内立方反ReO3结构的Cu3N的热力学性质.

Cu3N的晶格常数a随T和P的变化如图4所示.在给定P下a随T升高而增大，而在给定T下随P的增大而减小.这是因为对材料增加P与降低T，所起到的效应几乎是等同的.

从图5中得到了零压下Cu3N的体弹模量跟T的关系.当T<50K时，B几乎保持不变，当T> 50K时，随着T的增加，B急剧减小.由上，零压下T <50K时，a几乎保持不变，而T>50K，a随T的升高而急剧增大，导致了Cu3N的体弹模量随T升高而急剧减小.表3给出体弹模量BT及Debye温度Θ与T和压强的关系.两者都是随T的升高而减小，随P的增大而增大.通过Debye模型得出的零温零压下的体弹模量与用第一性原理(见表1)得出的结果相比误差为1.08%，两者结果基本相符.本文计算出在T=300K零压下，Cu3N的Debye温度Θ=327.62 K.

图6为Cu3N的热容量在给定压强下随T的变化曲线.Cp与CV的关系如(11)式.Cp与CV随T的升高而增大，随压强的增大而减小.CV在低温时变化较快，与T3成比例，是因为Debye模型的准谐近似.在高温时，准谐效应受限，受非谐效应的影响，CV趋向于Dulong-Pettit极限(对于单原子固体，CV～3NAKB)，即Cu3N的CV趋向于99.77 J·mol－1· K－1.这符合固体的共同性质.Cp在低温时较快变大，而在高温时并不趋于固定值.

图4 Cu3N的a与T，P的关系(a)a分别在0，1，2，3，4，5 GPa随T的变化;(b)a分别在0，100，200，300，400，500，600，700K随压强的变化

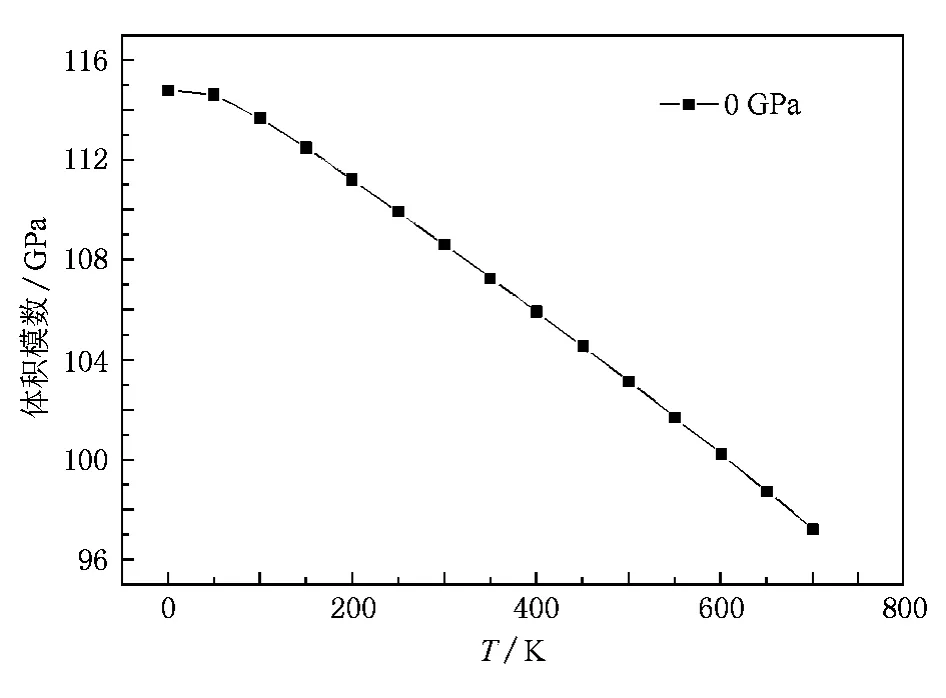
图5 零压下Cu3N的体弹模量与T的关系

图7为Cu3N的α随T与P的变化曲线.α为固定压力下平衡体积随T变化的变化.从图7中可以看出在给定压强下，Cu3N的α随T的升高而增大，低温时成指数形式增大;在高温时增大较慢，逐渐趋向于一常数.在给定T下，α随压强增大而减小.

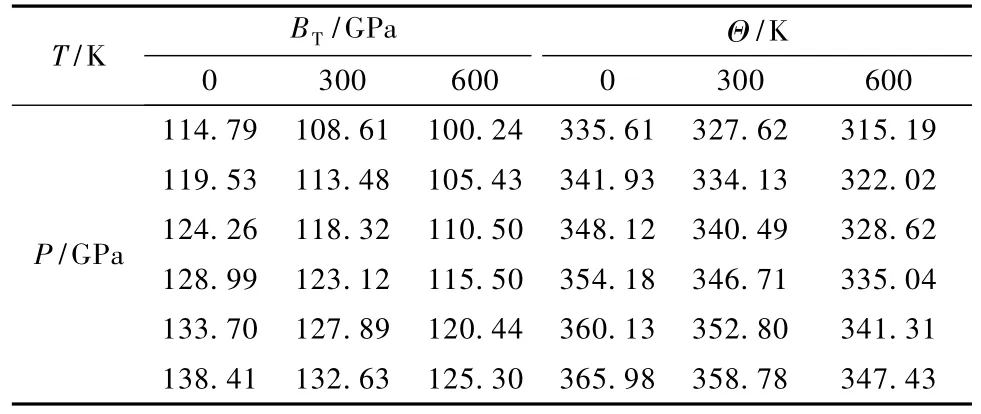
表3 不同T，P下Cu3N的体弹模量BT和Debye温度Θ

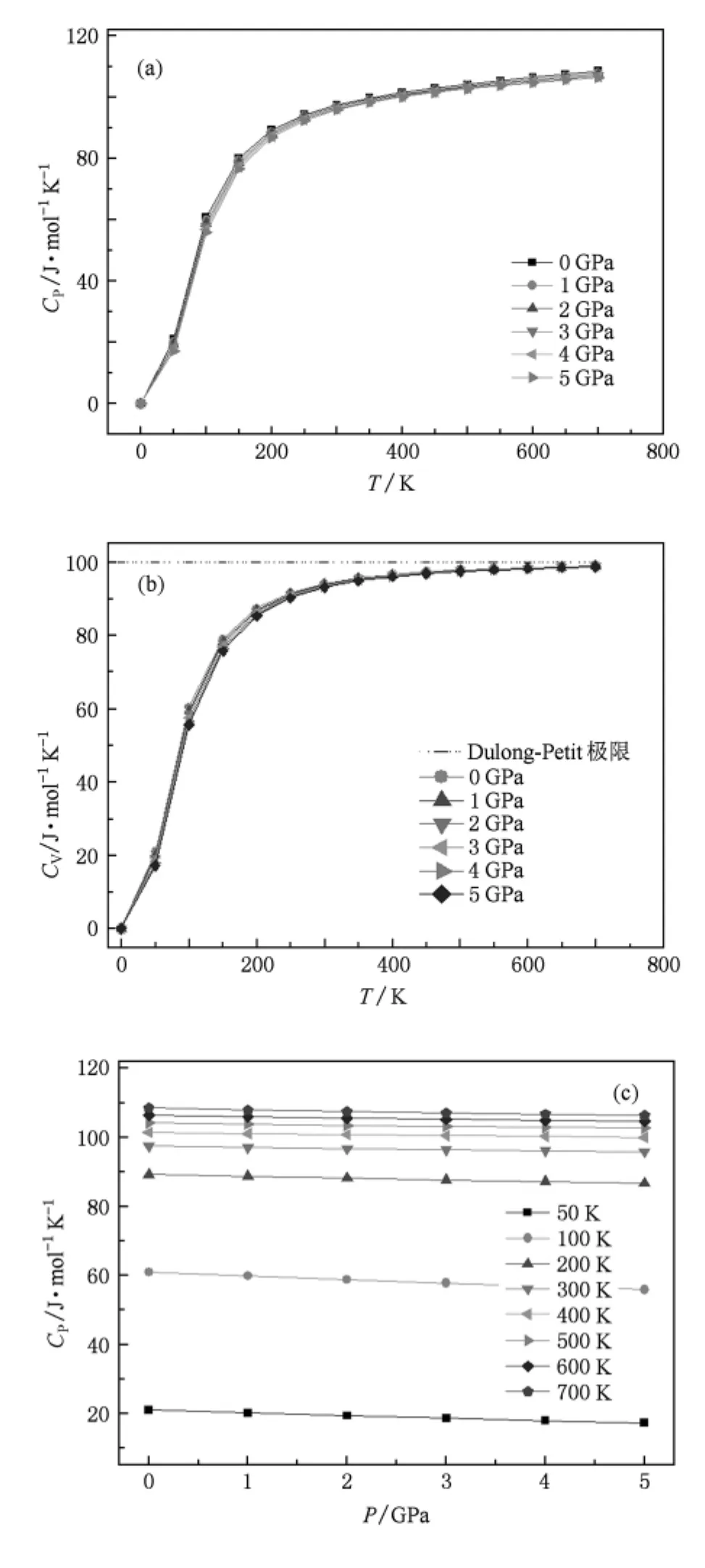
图6 Cu3N的热容量与T，P的关系(a)Cp分别在0，1，2，3，4，5 GPa随T的变化;(b)CV分别在0，1，2，3，4，5 GPa随T的变化; (c)Cp分别在50，100，200，300，400，500，600，700K随P的变化

图7 Cu3N的α与T，P的关系(a)α分别在0，1，2，3，4，5 GPa随T的变化;(b)α分别在0，100，200，300，400，500，600，700K随P的变化

4. 结论

本文利用基于密度泛函理论的全势线性缀加平面波方法计算了Cu3N的基本性质参数和弹性常数;利用准谐Debye模型研究了Cu3N的一些热力学性质.得到立方反ReO3结构的Cu3N在零温零压下当晶格常数a0=3.833时最稳定，与其他实验结果及计算结果基本一致.通过对晶格的三种形变，计算出弹性常数C11，C12，C44，所得结果与平面波赝势方法得到的结果一致，表明Cu3N在静态平衡晶格条件下是稳定的.进一步计算了Cu3N的弹性模量、剪切模量、杨氏模量以及Poisson比.在温度0—700K，压强0—5 GPa的范围内，研究Cu3N的热力学性质，得到晶格常数随P增大而减小，随T升高而增大;体弹模量与Debye温度随P增加而变大，随T升高而减小.在T=300K零压下，Cu3N的Debye温度Θ为327.62 K.另外，还得到了CV，Cp，α和T，P的关系，发现热容随着P增加而减小，热胀系数随P的增大而减小等变化规律.本文对于Cu3N材料的应用能起到一定的促进作用.

［1］Sieberer M，Khmelevskyi S，Mohn P 2006 Phys.Rev.B 74 14416

［2］Moreno-Armenta M G，Pe′rez W L，Takeuchi N 2007 Solid State Sci.9 166

［3］Borsa D M，Grachev S，Presura C，Boerma D O 2002 Appl. Phys.Lett.80 1823

［4］Hansen M，Anderko K 1958 Constitution of Binzry Alloys New York:McGraw-Hill

［5］Maruyama T，Morishita T 1995 J.Appl.Phys.78 4104

［6］Wang J，Chen J T，Miao B B 2006 J.Appl.Phys.100 103509

［7］Borsa D M，Boerma D O 2004 Surf.Sci.548 95

［8］Soto G，Diaz J A，de la Cruz W 2003 Mater.Lett.57 4130

［9］Soukup L，Sícha M，Fendrych F，Jastrabík L，Hubicka Z，Chvostová D，Síchová H，Valvoda V，Tarasenko A，Studnicka V，Wagner T，Novák M 1999 Surf.Coat.Technol.321 116

［10］Pierson J F 2002 Vacuum 66 59

［11］Moreno-Armenta M G，Martínez-Ruiz A，Takeuchi N 2004 Solid State Sci.6 9

［12］Hou Z F 2008 Solid State Sci.10 1651

［13］Yu W，Zhao J G，Jin C Q 2005 Phys.Rev.B 72 214116

［14］Yu W，Li L Y，Jin C Q 2005 J.Mater.Sci.40 4661

［15］Schwarz K，Blaha P，Madsen G K H 2002 Comput.Phys. Commun.147 71

［16］Pan Z J，Zhang L T，Wu J S 2005 Acta Phys.Sin.54 5308(in Chinese)［潘志军、张澜庭、吴建生2005物理学报54 5308］

［17］Blaha P，Schwarz K，Madsen G，Kvasnicka D，Luitz J 2008 WIEN2k An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties Vienna University of Technology Inst.of Physical and Theoretical Vienna

［18］Blanco M A，Francisco E，Luaa V 2004 Comput.Phys. Commun.158 57

［19］Chang J，Chen X R，Zhang W，Zhu J 2008 Chin.Phys.B 17 1377

［20］Wang H Y，Cui H B，Li C Y，Li X S，Wang K F 2009 Acta Phys.Sin.58 5598(in Chinese)［王海燕、崔红保、历长云、李旭升、王狂飞2009物理学报58 5598］

［21］Amrani B，Achour H，Louhibi S，Tebboune A，Sekkal N 2008 Solid State Commun.148 59

［22］Murnaghan F D 1944 Proc.Natl.Acad.Sci.U.S.A 30 5390

［24］Westbrook J H，Fleischer R L 1995 Intermetallic Compounds: Principles and Practice Volume I:Principles(London:John Wiley，Sons)195—210

［25］Liu N N，Song R B，Sun H Y，Du D W 2008 Acta Phys.Sin. 57 7145(in Chinese)［刘娜娜、宋仁伯、孙翰英、杜大伟2008物理学报57 7145］

PACC:0570C，6220D，7115A

*Project supported by the National Natural Science Foundation of China(Grant No.10974228)，the Research Foundation of Education Bureau of Hebei Province，China(Grant No.2009158)and the Yanshan University Doctor Foundation，China(Grant No.B321).

†E-mail:lish1990@sohu.com

First-principles calculation of elastic and thermodynamic properties of copper nitride*

Li Shi-Na†Liu Yong
(College of Science，Yanshan University，Qinhuangdao066004，China)
(Received 11 January 2010;revised manuscript received 30 January 2010)

A first-principles full-potential linearized augmented plane wave(FP-LAPW)method based on the density functional theory is applied to the study of the static equilibrium lattice structure as well as the elastic constants of the cubic anti-ReO3structural copper nitride(Cu3N).The quasi-harmonic Debye model，in which the phononic effects are considered，is used to investigate the thermodynamic properties of Cu3N.The pressure and temperature dependences of lattice constant，heat capacity and thermal expansion coefficient are successfully obtained.The bulk modulus and Debye temperature are also calculated at different pressures and temperatures.

thermodynamic properties，elastic constants，first-principles，Cu3N

book=701,ebook=701

*国家自然科学基金(批准号:10974228)、河北省教育厅科研基金(批准号:2009158)和燕山大学博士基金(批准号:B321)资助的课题.

†E-mail:lish1990@sohu.com