数据挖掘中决策树分类算法的研究

李如平

(安徽工商职业学院电子信息系，安徽合肥231100)

数据挖掘中决策树分类算法的研究

李如平

(安徽工商职业学院电子信息系，安徽合肥231100)

决策树方法是数据挖掘中一种重要的分类方法，决策树是一个类似流程图的树型结构，其中树的每个内部结点代表对一个属性的测试，其分支代表测试的结果，而树的每个叶结点代表一个类别。通过决策树模型对一条记录进行分类，就是通过按照模型中属性测试结果从根到叶找到一条路径，最后叶节点的属性值就是该记录的分类结果。

数据挖掘，分类，决策树

近年来，随着数据库和数据仓库技术的广泛应用以及计算机技术的快速发展，人们利用信息技术搜集数据的能力大幅度提高，大量数据库被用于商业管理、政府办公、科学研究和工程开发等。面对海量的存储数据，如何从中有效地发现有价值的信息或知识，是一项非常艰巨的任务。数据挖掘就是为了应对这种要求而产生并迅速发展起来的。数据挖掘就是从大型数据库的数据中提取人们感兴趣的知识，这些知识是隐含的、事先未知的潜在有用的信息，提取的知识表示为概念、规则、规律、模式等形式(姜灵敏等，2007)。

分类在数据挖掘中是一项非常重要的任务。分类的目的是学会一个分类函数或分类模型，把数据库中的数据项映射到给定类别中的某个类别。分类可用于预测，预测的目的是从历史数据记录中自动推导出对给定数据的趋势描述，从而能对未来数据进行预测(赵翔，2005)。分类算法最知名的是决策树方法，决策树是用于分类的一种树结构。

1 决策树介绍

决策树(decision tree)技术是用于分类和预测的主要技术，决策树学习是一种典型的以实例为基础的归纳学习算法，它着眼于从一组无次序、无规则的事例中推理出决策树表示形式的分类规则(赵翔，2005)。它采用自顶向下的递归方式，在决策树的内部节点进行属性的比较，并根据不同属性判断从该节点向下的分支，在决策树的叶节点得到结论。所以从根到叶节点就对应着一条合取规则，整棵树就对应着一组析取表达式规则(张桂杰，2005)。

把决策树当成一个布尔函数。函数的输入为物体或情况的一切属性(property)，输出为”是”或“否”的决策值。在决策树中，每个树枝节点对应着一个有关某项属性的测试，每个树叶节点对应着一个布尔函数值，树中的每个分支，代表测试属性其中一个可能的值。

最为典型的决策树学习系统是ID3，它起源于概念学习系统CLS，最后又演化为能处理连续属性的C4.5(C5.0)等。它是一种指导的学习方法，该方法先根据训练子集形成决策树。如果该树不能对所有给出的训练子集正确分类，那么选择一些其它的训练子集加入到原来的子集中，重复该过程一直到时形成正确的决策集。当经过一批训练实例集的训练产生一棵决策树，决策树可以根据属性的取值对一个未知实例集进行分类。使用决策树对实例进行分类的时候，由树根开始对该对象的属性逐渐测试其值，并且顺着分支向下走，直至到达某个叶结点，此叶结点代表的类即为该对象所处的类。

决策树是应用非常广泛的分类方法，目前有多种决策树方法，如 ID3，C4.5，PUBLIC，CART，CN2，SLIQ，SPRINT等。大多数已开发的决策树是一种核心算法的变体，下面先介绍一下决策树分类的基本思想决策树构造与剪枝，然后详细介绍ID3和C4.5算法及决策树算法的分析及改进等。

2 决策树构造与剪枝

决策树分类算法通常分为两个步骤，决策树生成和决策树剪枝。

2.1 决策树构造

决策树构造算法的输入是一组带有类别标记的例子，构造的结果是一棵二叉树或多叉树。二叉树的内部结点(非叶子结点)一般表示为一个逻辑判断，如形式为(ai=vi)的逻辑判断，其中ai是属性，vi是该属性的某个值。树的边是逻辑判断的分支结果。多叉树的内部结点是属性，边是该属性的所有取值，有几个属性值，就有几条边。树的叶子结点都是类别标记。

构造决策树的方法是采用自上而下的递归构造(毛国君等，2007)。以多叉树为例，它的构造思路是，以代表训练样本的单个结点开始建树，如果样本都在同一个类，则将其作为叶子结点，节点内容即是该类别标记。否则，根据某种策略选择一个属性，按照属性和各个取值，把例子集合划分为若干子集合，使得每个子集上的所有例子在该属性上具有同样的属性值。然后再依次递归处理各个子集。这种思路实际上就是“分而治之”的道理。二叉树同理，差别仅在于要如何选择好的逻辑判断。

构造好的决策树的关键在于如何选择好的逻辑判断或属性。对于同样的一组例子，可以有很多决策树符合这组例子(朱明，2008)。研究结果表明，一般情况下，树越小则树的预测能力越强。要构造尽可能小的决策树，关键在于选择合适的产生分支的属性。属性选择依赖于对各种例子子集的不纯度(Impurity)度量方法。不纯度度量方法包括信息增益(Information Gain)、信息增益比(Gain Ratio)、Gini-index、距离度量、x2统计、证据权重、最小描述长度等。不同的度量由不同的效果，特别是对于多值属性，选择合适的度量方法对于结果的影响是很大的。ID3，C4.5，C5.0算法使用信息增益的概念来构造决策树，而CART算法x则使用Gini-index，其中每个分类的决定都与前面所选择的目标分类相关。

2.2 决策树的剪枝

数据挖掘的对象是现实世界的数据，这些数据一般不可能是完美的，可能某些属性字段上缺值;可能缺少必须的数据而造成数据不完整;可能数据不准确、含有噪声甚至是错误的，所以要讨论噪声问题。基本的决策树构造算法没有考虑噪声，生成的决策树完全与训练例子拟合。有噪声情况下，完全拟合将导致过分拟合，即对训练数据的完全拟合反而不具有很好的预测性能。剪枝是一种克服噪声的技术，同时它也能使树得到简化而变得更容易理解。

1)两种基本的剪枝策略。

①前期剪枝(Forward-Pruning)是在树的生长过程完成前就进行剪枝(马丽等，2008)。在树的生长过程中，决定是继续对不纯的训练子集进行划分还是停机。

例如某些有效统计量达到某个预先设定的阈值时，节点不再继续分裂，内部节点成为一个叶子节点。叶子节点取子集中频率最大的类作为自己的标识，或者可能仅仅存储这些实例的概率分布函数。前期剪枝会引起树在不完全成熟之前停止工作，即树可能在不应停止的时候而停止扩展，或称之为horizon效应，而且，选取一个适当的阈值是困难的。较高的阈值可能导致过分简化的树，而较低的阈值可能使树简化的太少。即使这样，预先修剪对大规模的实际应用还是值得研究的，因为它相当高效。人们有望在未来的算法中解决horizon效应。

②)后期剪枝(Post-Pruning)是当决策树的生长过程完成之后再进行剪枝(马丽等，2008)。它是一种拟合-化简(Fitting-and-simplifying)的两阶段方法(毛国君等，2007)。首先生成与训练数据完全拟合的一棵决策树，然后由下向上从树的叶子开始剪枝，逐步向根的方向剪。剪枝时要用到一个测试数据集合，如果存在某个叶子剪去后测试集上的准确度或其它测度不降低(不变得更坏)，则剪去该叶子，否则停机。

如果节点的子树不应按某种规则被修剪，则由下向上的评价规则将使该节点避免被按同一规则修剪。与此相对的是自上向下的策略，即从根开始依次修剪节点，直到无法修剪为止。这样作的风险在于，按某种规则剪掉了某个节点，但其子类是不应按这一规则被剪掉的。

2)对树进行修剪优化时应遵循的原则。

①最小描述长度原则(MDL)(张桂杰，2005)。它的思想是最简单的解释是期望的，做法是对决策树进行二进位编码。编码所需二进位最少的树即为“最佳剪枝树”。

②期望错误率最小原则(张桂杰，2005)。它的思想是选择期望错误率最小的子树剪枝，即对树中的内部节点计算其剪枝/不剪枝可能出现的期望错误率，比较后加以取舍。

③奥卡姆剃刀原则。如无必要，勿增实体(朱明，2008)。即“在与观察相容的理论中，应当选择最简单的一个”，决策树越小就越容易被理解，其存储与传输的代价也就越小。

3 ID3算法

ID3算法是1986年Quinlan提出的一个著名决策树生成方法，是目前引用率很高的一种算法。ID3算法是运用信息熵理论，选择当前样本集中最大信息增益的属性值作为测试属性;样本集的划分则依据测试属性值进行，测试属性有多少不同取值就将样本集划分为多少子样本集，同时，决策树上相应于该样本集的节点长出新的叶子节点。由于决策树的结构越简单越能从本质的层次上概括事物的规律，期望非叶节点到达后代节点的平均路径总是最短，即生成的决策树的平均深度最小，这就要求在每个节点选择好的划分。系统的不确定性越小，信息的传递就越充分。ID3算法根据信息理论，采用划分后样本集的不确定性作为衡量划分好坏的标准，用信息增益值度量:信息增益值越大，不确定性越小。因此，算法在每个非叶节点选择信息增益最大的属性作为测试属性。

ID3算法将对挖掘样本集分为训练样本集和测试样本集，决策树的构建是在对训练样本集的学习上产生的，决策树生成之后，再运用测试样本集对树进行后剪技，将分类预测准确率不符合条件的叶节点剪去。

1)信息理论(Informaiton theory)和熵(Entropy)。信息论是C.E Shannon为解决信息传递(通信)过程问题而建立的理论，一个传递信息的系统是由发送端和接收端以及连接两者的通道三者组成。熵是对事件对应的属性的不确定性的度量。一个属性的熵值越小、子集划分的纯度越高，熵值熵越大，它蕴含的不确定信息越大，约有利于数据的分类(张桂杰，2005)。

2)信息增益(Informmation Gain)。信息增益基于信息论中熵(Entropy)的概念，是指期望信息或者信息熵的有效减少量(通常用“字节”衡量)，根据它能够确定在什么样的层次上选择什么样的变量来分类(毛国君等，2007;朱明，2008)。ID3总是选择具有最高信息增益(或最大熵)的属性作为当前结点的测试属性。该属性使得对结果划分中的样本分类所需的信息量最小，并反映划分的最小随机性或“不纯性”。信息增益计算如下:

设S是s个训练样本数据集，S中类标识属性具有m个不同值，定义m个不同类Ci(i=1，2，3…，m)。设si是类Ci中的样本数。对一个给定的样本分类所需的期望信息由下式得出:

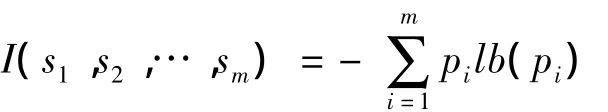
其中pi是任意样本属于Ci的概率，一般可用si/s来估计。

设属性A具有n 个不同值{a1，a2，…，an}，可以用属性A将S划分为n个子集{S1，S2，…，Sn}，其中Sj包含S中这样一些样本，它们在A上具有值aj。如果A作为测试属性，则这些子集对应于由包含集合S的结点生长出来的分支。

设sij是子集Sj中类Ci的样本数。根据由A划分成子集的熵由下式给出:

根据上面的期望信息计算公式，对于给定的子集Sj，其期望信息由下式计算:

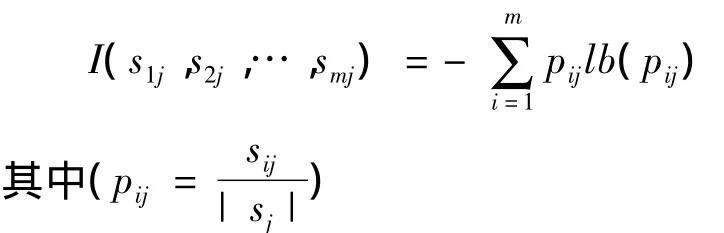
对属性A作为决策分类属性的度量值即信息增益可以由下面的公式得到:

3)ID3算法的分析。ID3通过不断的循环处理，逐步求精决策树，直至找到一个完全正确的决策树。ID3算法构造的决策树是从顶向下归纳形成了一组类似If…Then的规则。其最原始的程序只是用来区分象棋中的走步，所以区分的类别只有两种，即真或假，其属性值也是一些离散有限的值，页今ID3算法已发展到允许多于两个类别，而其属性值可以是整数或实数。其优缺点总结如下:

①优点。ID3在选择重要特征时利用了信息增益的概念，算法的基础理论清晰，使得算法较简单，该算法的计算时间是例子个数、特征个数、结点个数之积的线性函数。而且搜索空间是完全假设空间，目标函数必在搜索空间中，不存在无解的危险。全盘使用训练数据，而不像候选剪除算法一个一个地考虑训练例。这样做的优点是可以利用全部训练例的统计性质进行决策，从而抵抗噪音。

②缺点。信息增益的计算依赖于特征值数目较多的特征，这样不太合理，一个简单的办法对特征进行分解，可以把特征值统统化为二值特征。ID3对噪声较为敏感。Quinlan定义训练例子中的错误就是噪声。它包括两个方面，一是特征值取错，二是类别给错。当训练集增加时，ID3的决策树也会随之变化。在建树过程中各特征的信息增益随例子的增加而变化，这对渐近学习不够方便。

4 C4.5 算法

C4.5(Classsification 4.5)算法是 Quinlan 在1993年提出的，它既是ID3算法的后继，也成为以后诸多算法的基础。除了拥有ID3算法的功能外，C4.5算法引用了新的方法并增加了新的功能。在应用于单机的决策树算法中，C4.5算法不仅分类准确率高而且速度快。

C4.5算法在ID3的基础上增加了信息增益比例的概念和连续型属性，属性值空缺情况的处理，对树剪枝也有了较成熟的方法，通过使用不同的修剪技术以避免树的过度拟合，它克服了ID3在应用中的不足。首先用信息增益率来选择属性，克服了用信息增益选择属性时偏向于选择取值多的属性的不足。其次，能够完成对连续属性的离散化处理，还能够对不完整的数据进行处理。C4.5算法采用的知识表示形式为决策机构树，并最终可以形成产生式规则。

1)信息增益比例的概念。信息增益比例是在信息增益概念基础上发展起来的，一个属性的信息增益比例用下面的公式给出:

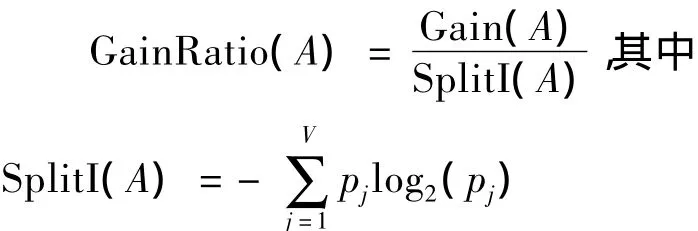
这里设属性A具有v个不同值{a1，a2，…，av}。可以用属性A将S划分为v个子集{S1，S2，S3}，其中Sj包含S中这样一些样本，它们在A上具有值aj。假如我们以属性 A的值为基准对样本进行分割，SplitI(A)就是前面熵的概念(毛国君等，2007;朱明，2008)。

2)合并具有连续值的属性。ID3算法最初假定属性离散值，但在实际应用中，很多属性值是连续的。针对连续属性值，C4.5首先根据属性的值，对数据集排序，用不同的阈值将数据集动态地进行划分，当输入改变时，取两个实际值中的中点作为一个阈值，取两个划分，所有样本都在这两个划分中，得到所有可能的阈值、增益及增益比，在每一个属性会变为俩个取值，即小于阈值或大于等于阈值。

针对属性有连续数值的情况，比如说A有连续的属性值，则在训练集中可以按升序方式排列a1，a2，…，am。如果 A共有 n种取值，则对每个取值vj(j=1，2，…，n)将所有的记录进行划分。这些记录被划分成为两个部分:一部分在vj的范围内，而另一部分则大于vj。针对每个划分分别计算增益比率，选择增益最大的划分来对相应的属性进行离散化。

3)规则的产生。一旦树被建立，就可把树转化成If-Then规则。规则存储于一个二维数组中，每一行代表树中的一个规则，即从根到叶之间的一个路径，表中的每列存放着树中的结点。

5 决策树分类算法的分析

基于决策树的分类算法自提出至今，种类不下几十种。各种算法在执行速度、可扩展性、输出结果的可理解性及分类预测的准确性等方面各有千秋。决策树分类算法的发展可分为这样几个阶段:首先，最早出现的ID3算法采用信息熵原理选择测试属性分割样本集，只能处理具有离散型属性和属性值齐全的样本，生成形如多叉树的决策树。后来出现的C4.5算法经过改进，能够直接处理连续型属性，能够处理属性值空缺的训练样本。ID3系列算法和C4.5系列算法在对训练样本集的学习中尽可能多地挖掘信息，但其生成决策树分枝较多，规模较大。为了简化决策树算法，提高生成的决策树的效率，又出现了一些其它决策树算法。

决策树分类算法的优点主要是能生成可以理解的规则，计算量相对来说不是很大，可以处理多种数据类型，决策树可以清晰的显示哪些属性比较重要。与此同时它也存在一些缺点如对连续性的字段比较难预测，对有时间顺序的数据，需要很多预处理的工作，当类别太多时，错误可能就会增加的比较快。

6 决策树分类算法的改进

针对决策树分类算法的缺点，下面将从属性的选择，如何对连续性属性进行离散化等算法改进方面进行介绍。

1)属性选择。为了避免噪声和干扰属性对数据分类的影响，在建立决策树之前先进行对属性重要性排序，再用神经网络技术对其中最重要的若干属性进行训练并检验其预测精度，然后属性重要性次序向两端分别加减一个邻近的属性再进行训练及检验并和原检验结果比较，这样反复多次直到找到分类效果最佳的n个属性为止，这样得到n个分类效果最好的属性。

2)连续属性离散化。离散化是分类过程中处理连续性的一种有效方法。离散化的效率和有效性直接影响到后续机器学习算法的效率和性能。很多分类规则只能处理离散属性，如ID3算法，对连续属性进行离散化是一个必要的步骤。C4.5虽能够处理连续属性，但离散化也是系统集成的一个重要步骤。离散化不仅可以缩短推导分类器的时间，而且有助于提高数据的可理解性，得到解精度更高的分类规则。

从优化的角度可以将离散化方法分为两类:局部方法和全局方法。局部方法每次只对一个属性进行离散，而全局方法同时对所有属性进行离散。局部离散方法相对简单，全局方法因为考虑了属性间的相互作用往往可以得到比局部化方法更好的结果，但全局方法计算代价很高。

7 结束语

通过以上研究和分析，可以得出构造好的决策树关键在于如何选择好的逻辑判断和属性。随着数据库和数据仓库技术的广泛应用，数据的海量增加，决策树技术的效率有待提高，针对实际问题时，需要对决策树数据挖掘方法在适应性、容噪性等方面进行适当的改进。

但小容，陈轩恕，刘飞，柳德伟.2009.数据挖掘中决策树分类算法的研究与改进［J］.软件导刊，8(2):41-43.

董贺，荣光怡.2008.数据挖掘中数据分类算法的比较分析［J］.吉林师范大学学报(自然科学版)，4:107-108.

姜灵敏，马于涛.2007.信息资源聚合与数据挖掘［M］.广州:华南理工大学出版社，12-18.

马丽，陈桂芬.2008.基于数据挖掘的决策树算法应用研究［J］.农业网络信息，11:45-47.

毛国君，段立娟，王实，石云.2007.数据挖掘原理与算法(第二版)［M］.北京:清华大学出版社，120-131.

张桂杰.2005.数据挖掘决策树分类算法的研究与应用［D］.长春:长春理工大学.

赵翔.2005.数据挖掘中决策树分类算法的研究［D］.镇江:江苏科技大学.

朱明.2008.数据挖掘(第2版)［M］.合肥:中国科学技术大学出版社，63-102.

Research of Decision Tree Classification Algorithm in Data Mining

LI Ru-ping
(Anhui Business Vocational College，Department of Electronic and Information，Hefei，AH 231100，China)

Decision tree algorithm is one of the most important classification measures in data mining.Decision tree classifier as one type of classifier is a flow-chart like tree structure，where each intenal node denotes a test on an attribute，each branch represents an outcome of the test，and each leaf node represents a class.The method that a decision tree model is used to classify a record is to find a path that from root to leaf by measuring the attributes test，and the attribute on the leaf is classification result.

data mining;classification;decision tree

TP311.13

A

1674-3504(2010)02-192-05

10.3969/j.issn.1674-3504.2010.02.015

2010-02-28

李如平(1973—)，男，安徽肥东人，讲师，硕士，主要研究方向:计算机应用技术、信息管理。