自适应约束惩罚的粒子群聚类算法

张国英, 刘冠洲, 徐 宁, 周俊武

(1.中国矿业大学(北京) 计算机系 北京100083;2.北京矿冶研究总院 北京100044)

自适应约束惩罚的粒子群聚类算法

张国英1, 刘冠洲1, 徐 宁2, 周俊武2

(1.中国矿业大学(北京) 计算机系 北京100083;2.北京矿冶研究总院 北京100044)

提出了基于惩罚约束问题的群体智能聚类算法PCSI,不必穷尽搜索样本集,利用粒子群算法的优化搜索机制在数据集中有指导地随机搜索聚类中心向量,能够以较小的计算代价确定样本集的类别数.有约束优化过程的罚函数为两部分之和:①目标函数,各样本与其类别中心的均方误差;②自适应惩罚项,即数据集的边界作为粒子群移动的约束条件,对约束违反程度进行惩罚.为降低不平衡数据集的影响,按照数据集的方差和模糊高斯函数,将样本到其类别中心的距离进行模糊映射,归一化到[0,1]区间.粒子群优化方法免去了传统方法的求导计算.聚类IRIS数据集和Reuters-21578文档集以验证算法的有效性,对大规模数据聚类有明显优势.

粒子群算法;智能优化;自适应罚函数

0 引言

群体智能优化搜索算法在机器学习领域的作用日趋重要,粒子群算法作为其中的成员,能够有助于确定无监督聚类问题的类别数目.

聚类问题转化为以各样本与其类别中心的均方误差为目标函数的优化问题,搜寻类别中心的过程即逐步降低均方误差M SE并使其最小化,同时考虑类别范围的约束.聚类过程可建模为非线性约束优化问题,许多传统算法(如梯度映射法、梯度下降法、惩罚函数法及障碍函数法等)能够对非线性约束优化问题进行求解,但单纯使用这些方法或者效率低或者适用范围受限.

计算智能家族的各种优化搜索算法求解过程不依赖于目标函数的解析性质,具有解的多样性和计算的并行性等优点,能较好解决上述传统算法易于陷入局部最优的缺点[1],对优化问题没有求导的数学计算,可以处理任意形式的目标函数和约束.用优化搜索方法求解约束优化问题时,首先把个体代入可行域,然后在可行域内找到尽可能优化的解.目前,惩罚函数法是最广泛的约束问题处理方法.

罚函数通过调整罚因子实现目标函数和约束之间的平衡,罚因子过小,对不可行解的惩罚不够,导致过大的解空间;罚因子过大,使罚函数对应的优化曲面更加复杂,虽然有利于获得可行解,但不利于获得优良解.本文用搜索过程中获得的信息反馈指导罚因子的调整,并采用适应性罚函数[2-3].遗传算法和粒子群算法是基于生物进化思想[4-5]的两个典型的优化搜索方法,将优化搜索过程模拟成物种进化过程.遗传算法对复杂问题的编码较困难,操作复杂、效率较低,对不同的优化问题往往需要设计不同交叉或变异方式.Kennedy和Eberhart提出的粒子群优化算法(particle swarm op timization)在许多优化问题中的应用更为成功[6].

1 群体智能聚类基础

聚类的主要任务是找到聚类类数和各类别中心,K-means等硬聚类算法穷尽搜索整个训练集,反复计算各类别中心与所有样本间的距离,不断更新类别中心,使所有样本与其类别中心的距离之和最小化.样本个数越多或样本的特征向量维数越高,计算复杂性就越高.

1.1 聚类的目标函数

1)样本集C均值(样本数N)

2)样本集C中第j类Cj(样本数Nj)的类别中心

3)Cj的方差,反映第j类的分散度

4)均方误差归一化

σj即为类别j的均方误差M SE,聚类的过程是使各类别及整个样本集的均方误差最小化.由于不同样本集的分布差别很大,呈现出不同的密度或尺寸大小.若聚类过程降低均方误差M SE的绝对值,则密度或尺寸较小的聚群被忽略,大的聚集会被分割.用模糊高斯函数将样本与其类别中心的距离进行归一化处理,映射到[0,1]区间内.在保留聚类样本集各类别的区分特征的条件下,将大小、紧密性不同的类别放在相同判别尺度下度量.

第j个聚类集Cj归一化后的均方误差为

假设类别数为J,训练集归一化后均方误差为

1.2 粒子群算法

粒子群优化算法使用并行结构策略[1,6],粒子种群在搜索空间快速移动,每个粒子代表优化问题的一个候选解.算法随机但有指导性地加强目标函数在多维空间的搜索能力,具有最优适应度值的候选解是目标函数的优化解.PSO具有全局搜索和快速收敛的特点,PSO种群中第i个粒子的第d维分量在t+1次迭代的移动速度由公式(6)决定,

粒子的移动速度由3部分构成:记忆项,各粒子前一次的速度;认知项,各粒子历史过程到达的最优位置;社会项,整个种群到达的最优位置.

粒子移动后的位置由公式(7)决定,即前一位置与移动速度之和

确定粒子种群的最优位置Pg和粒子i的历史最优位置Pi是PSO优化的关键.种群在搜索空间内全局优化Pg并指导搜索,直到达到迭代次数或满足误差阈值.

粒子群聚类以目标函数(即样本与其类别中心的均方误差为适应度函数)决定其搜索方向.样本集进行映射后,每个类别分别在不同位置聚集,考虑聚集范围的约束对类别中心的搜寻有明确的指导作用.粒子群以此为约束条件,对违反约束的移动进行惩罚[7],迫使粒子群回归恰当范围,同时粒子群的迭代次数作为惩罚因子,使聚类过程自适应性地降低迭代次数.

在D维欧式空间RD中,聚类方法依样本的相似性自动将N个样本分成J个聚类,并确定其类别的中心向量.集合{x1,x2,…,xNj}表示任一聚类Cj的样本子集,聚类Cj的类别中心向量亦为D维,即zj=[zj1, zj2,…,zjD].PSO种群的任一粒子代表J个类别的中心向量,对于D维空间的样本聚类,每个粒子的变元向量为J×D维,

2 罚函数及约束条件

2.1 适应性惩罚函数

将约束优化问题转化为等价的无约束优化问题,罚函数法是最常用的约束处理技术,将目标函数和约束综合为一个罚函数,典型的罚函数[2]为

其中,f(x)为优化问题的目标函数,Gi(x)和Hj(x)分别为不等式约束和等式约束函数,ri和sj为相应的罚因子,Gi(x)和Hj(x)普通形式为:

对于不可行解,违反约束的程度越强,相应的Gi(x)和Hj(x)函数值就越大,则罚函数φ(x)的值就越大.罚因子过小,对不可行解的惩罚不够,获得的解可能为不可行解;罚因子过大,会使罚函数对应的优化曲面复杂化,虽然有利于获得可行解,但不利于获得优良解.合理设置罚因子是利用罚函数法求解约束优化问题的关键.

把迭代搜索过程中获得的信息反馈指导罚因子的调整[3],包括可行解和不可行解的信息,采用通用性更强的适应性罚函数降低约束优化的迭代次数,提高解的精度.适应性惩罚函数定义为

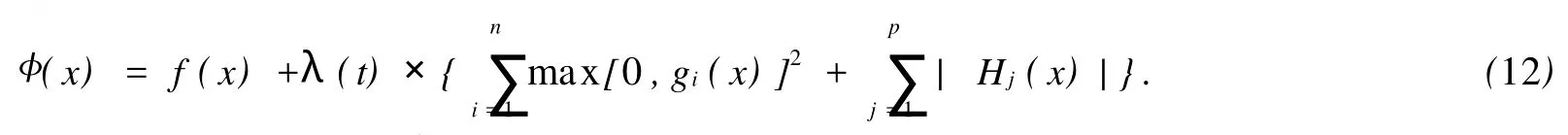
λ(t)在迭代过程随迭代次数t更新的方式为[3]

其中,β1>1,β2<1,case1表示迭代至第t代时找到的最好个体均为可行解,由罚因子过大导致,可适当减小罚因子来降低对不可行解的惩罚压力;case2表示迭代至第t代时找到的最好个体均为不可行解,表示罚因子过小,需适当增大罚因子来增强对不可行解的惩罚;case3表示迭代至第t代时找到的最好个体包括不可行解和可行解,表示罚因子基本合适,可保持.

2.2 群体智能聚类的罚函数

粒子群聚类的目标函数为粒子种群中所有粒子位置与其类别中心的均方误差值,聚类过程使均方误差最小化,

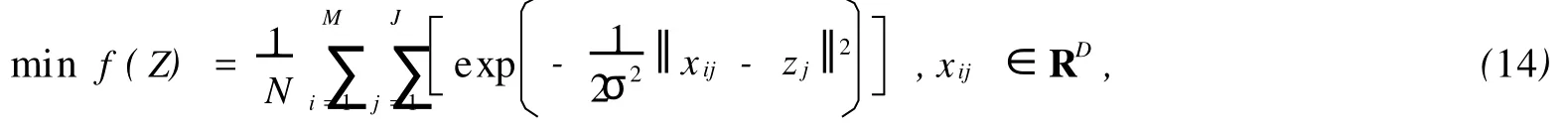
其中,M为粒子种群的粒子数,J为样本集合聚类的类别数目,xij表示种群第i个粒子的第j个类别中心分量.每个粒子位置到其类别中心的距离应小于粒子位置与样本集均值的距离,否则表示粒子的移动离开了训练样本集.优化解Z使均方误差最小,并代表搜索到的所有类别中心的向量集合.

约束条件没有等式约束条件,仅表示为不等式约束函数

其中,xi表示种群的第i个粒子,约束粒子群聚类的适应度函数除考虑粒子与其类别中心的均方误差外,需对粒子移动违反约束的情况进行惩罚,适应度函数表述为均方误差函数与惩罚函数之和,采用适应性惩罚函数[3]

3 自适应约束惩罚的群体智能聚类算法

基于约束惩罚的群体智能聚类算法(PCSI)可以自动确定样本集的聚类个数,并对违反约束的情况进行自适应惩罚调整,如果找到的最好个体均为可行解,表示罚因子已足够大,如果找到的最好个体均为不可行解,表示罚因子非常小.PCSI算法步骤如下[7]:

1)初始化种群中M个粒子的位置和速度.每个粒子代表的聚类数随机产生且互不相同,每个粒子的变元维度也各不相同,为类别数×维数D,初始速度向量在小范围内随机产生;

2)根据适应度函数式(16)对粒子进行评价,适应度函数为均方误差目标函数与自适应罚函数之和;

3)每个粒子在迭代的过程中获得的自身历史最小适应度值的位置为其局部优化指导Pi;

4)种群粒子取得最小适应度值的位置为全局优化指导Pg;

5)根据式(6)和式(7)进行粒子速度和位置的更新;

6)重复步骤2)～5),粒子群在两次迭代中的适应度值之差小于阈值,则具有最小适应度值的粒子所代表的聚类数为训练样本集的类别数;

7)随机产生M个粒子的初始种群,每个粒子的向量维度为:类别数(步骤6)确定)×维数D,其中第一个粒子的初始位置为步骤6)具有最小适应度值的粒子位置,初始速度向量在小范围内随机产生.

8)重复步骤2)～5),粒子群在两次迭代中的适应度值之差小于阈值,输出全局优化指导Pg及其适应度值.Pg代表的类数目为聚类数目,向量Pg代表各类别的中心位置.

4 实验及分析

以Reuters-21578文本数据集的Top10子集和IRIS数据集进行聚类实验,验证约束惩罚的群体智能聚类算法的有效性,进行了约束惩罚聚类和无约束群体智能聚类的对照实验.

IRIS数据集分为3个类别,共150个样本,Top10数据集包含earn,Acq,Money-fx,Grain,Crude, Trade,interest,w heat,ship和corn共10个类别.PCSI聚类算法主要解决聚类类别数和搜索出各类别的中心向量这两个主要问题,式(16)为粒子群优化的目标函数,采用自适应罚函数,迭代过程严格限制粒子的移动范围在训练样本集合内各类别的内部,对移动出可行域的运动进行惩罚.

PCSI算法分两步进行:首先搜索样本集的类别数;然后搜索类别中心向量.PCSI算法的参数设置为[8]:最大迭代次数tmax=150;搜索样本集类别数时,粒子种群数目M=5;搜索类别中心向量时,粒子种群数目M =10;学习因子c1=c2=0.5,自适应性罚因子的系数β1=5且β2=0.2.

粒子群初始迭代时在全局范围较大速度寻优,在后续迭代过程降低移动速度,能够在最优值的邻域内逐步逼近最优解,因为较大的移动速度在优化解邻域容易震荡.

4.1 聚类实验结果

对基于约束惩罚的群体智能聚类算法进行聚类实验测试,确定数据集的聚类个数时,种群的粒子数M设置为5.对于IRIS数据集,5个粒子分别代表样本集类别数2,3,4,5,6;对于Top10数据集,5个粒子分别代表样本集类别数6,8,10,12,14.采用自适应罚函数聚类,表1和表2分别为5个种群粒子对IRIS数据集和Top10数据集聚类的实验结果,即每个粒子在聚类结束时的适应度值和迭代次数.

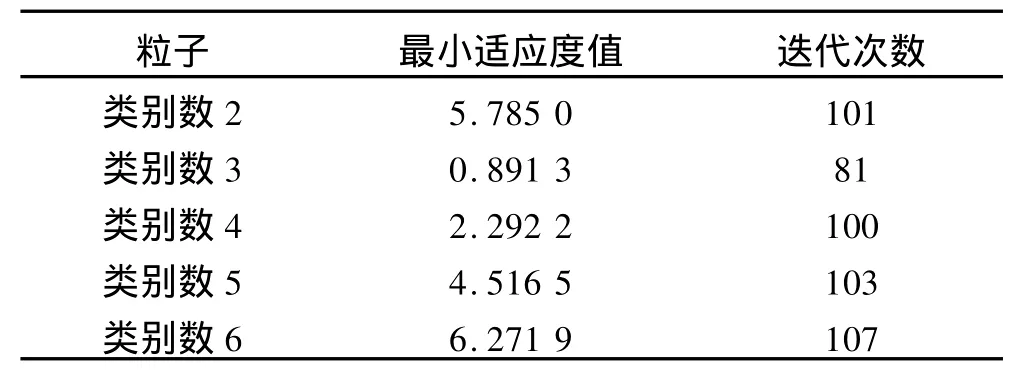
表1 PCSI算法对IRIS数据集聚类的实验结果Tab.1 Experimental results of PCSIclassifying IRIS

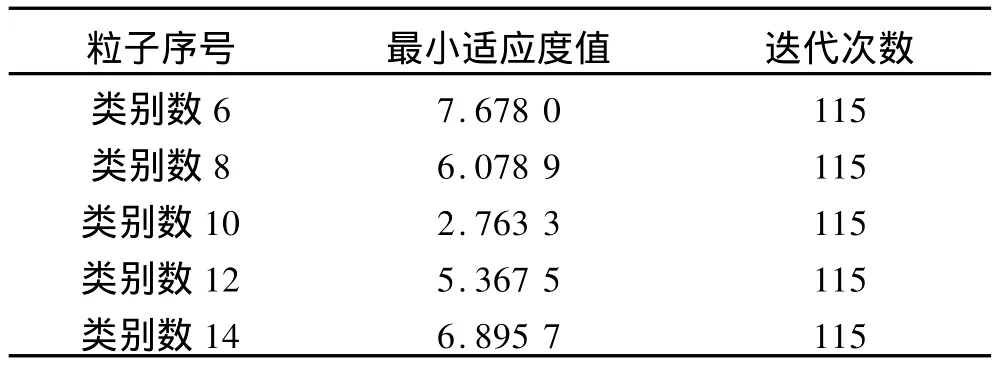
表2 PCSI算法对Top10数据集聚类的实验结果Tab.2 Experimental results of PCSIclassifying Top10

表1中第2个粒子代表样本集有3个类别,种群中获得了最小的适应度值,且迭代时收敛最快.Top10数据集聚类收敛较慢,表2仅取115次迭代的实验结果作为对比,第3个粒子代表样本集有10个类别,在迭代过程中适应度值一直低于其他粒子.IRIS数据集和Top10数据集的聚类结果均符合数据集的分布.

4.2 约束与无约束聚类实验

确定聚类个数后,继续搜索类别的中心向量.设置种群的粒子数为10,并与无约束粒子群聚类算法CPSO进行对照实验,具体见图1,图2.

PCSI聚类IRIS数据集时迭代到42代时收敛,其适应度值为0.64.而CPSO在迭代到50代时基本收敛,适应度值为0.74.PCSI的聚类时间是CPSO的84%,适应度值下降10.9%.

PCSI聚类Top10数据集时,迭代过程其适应度值一直低于CPSO,迭代到50代时PCSI算法基本收敛,适应度值为1.621.而CPSO的适应度值为2.491,适应度值下降56.2%.约束惩罚的群体智能聚类算法比无约束智能聚类算法的聚类效率有明显提高.

[1] Kennedy J,Eberhart R C.Particle swarm op timization[C]//Proceedings of 1995 IEEE International Conference Neural Networks.Perth,1995:1942-1948.

[2] 王凌,何锲,金以慧.智能约束处理技术综述[J].化工自动化及仪表,2008,35(1):1-7.

[3] Wang Y,Cai Z X,Guo GQ.M ulti-objectiveop timization and hybrid evolutionary algo rithm to solve constrained optimization p roblem s[J].IEEE Trans on System s,Man and Cybernetics,Part B:Cybernetics,2007,37(3):560-575.

[4] Montes EM,Coello C A C.A simp le multimembered evolution strategy to solve constrained op timization p roblems[J]. IEEE Transon Evolutionary Computation(S10892778X),2005,9(1):1-17.

[5] Bandyopadhyay S,Maulik U.Genetic clustering fo r automatic evolution of clusters and app lication to image classification [J].Pattern Recognition,2002,35:1197-1208.

[6] Om ran M,Engelbrecht A,Salman A.Particle swarm op timization method for image clustering[J].Journal of Pattern Recognition and A rtificial Intelligence,2005,19(3):297-322.

[7] Zhang Guoying,Liu Yalu,Sha Yun,et al.A new cluster algo rithm based on constrained particle swarm op timization [J].Journal of Computational Information System s,2008,4(3):1037-1040.

[8] Shi Y,Eberhart R C.Parameter selection in particle swarm op timization[C]//Evolutionary Programming V II:Proceedings of 7th Annual Conference on Evolutionary Programming.New York,1998:591-600.

Particle Swarm Clustering Algorithm Based on Adapative Constrained Penalty

ZHANG Guo-ying1, L IU Guan-zhou1, XU Ning2, ZHOU Jun-w u2
(1.Department of Com puter,China university of M ine Technology(Beijing),Beijing 100083,China; 2.Beijing General Research Institute of M ine and M etallurgy,Beijing 100044,China)

A clustering algorithm based on punishing constraint of swarm intelligence(PCSI)is p roposed.Directed by the natureof PSO,PCSIcould random ly search the centersof clustersand obtain the number of clustersw ith fewer computation cost.Penalty function consistsof two components:the first one is the objective function,mean square error(M SE)between every samp le and its cluster center,and the second one is adap tive penalty function,the boundary of data set could be used to constrain particle movement,and the circum stance of violating constraints is punished by corresponding constraint function w ith differential coefficient.In order to decrease the effect of unbalanced data set,the distance of samp le to its cluster center is normalized into space[0,1]by the variation of data set and fuzzy Gaussian function.PCSIisevaluated by clustering IRIS data set and Reuters-21578 text set,and the clustering perfo rmance of PCSIis superio r to non-constrained algo rithm in large size data set.

PSO algorithm;constraint op timization;adap tive penalty function

TP 301.6

A

1671-6841(2010)02-0047-06

2009-11-17

张国英(1968-),女,副教授,博士,主要从事人工智能研究,E-mail:zhangguoying1101@163.com.