两种运行方式下灌溉渠道的非恒定流数值模拟
2010-09-05吕宏兴余国安
韩 宇,吕宏兴,余国安
(1.西北农林科技大学水利与建筑工程学院,陕西杨凌 712100;2.中国科学院地理科学与资源研究所,北京 100101)
两种运行方式下灌溉渠道的非恒定流数值模拟
韩 宇1,吕宏兴1,余国安2
(1.西北农林科技大学水利与建筑工程学院,陕西杨凌 712100;2.中国科学院地理科学与资源研究所,北京 100101)
为了保证灌溉渠道运行安全、合理调配水量,研究单一渠段的非恒定流过渡过程对促进灌溉管理水平是十分必要的。通过考虑灌溉渠道的不同运行方式以及节制闸的不同调控等综合影响,按照灌区常用的渠段上游常水深运行和下游常水深运行2种运行方式,应用渠道非恒定流数值模拟的特征线法及矩形网格计算格式,对梯形断面渠段由于不同闸门调控方式所引起的非恒定流过渡进行模拟,比较2种运行方式以及预报出各级节制闸调闸时间提前量,全面地反映系统动态并且较明确地模拟闸门调节过程。
上游常水深运行;下游常水深运行;闸门调控;明渠非恒定流;数值模拟
渠道系统由一系列明渠渠段(又称渠池)组成,渠道的运行控制就是调控整个渠道水流和水深的变化,保证流量变化时渠道仍要保持较稳定的水位,这才能有利于渠坡和衬砌的稳定安全并确保配水的合理性。一般采用的运行方式有两种,即上游常水深运行和下游常水深运行。选择渠道运行控制的方法可以是就地人工控制、就地自动控制或者检测控制。当前,我国传统渠道还只都采用就地人工控制,渠系自动化国外研究较早,并且自动化灌溉在国外已有相当规模,我国已在援建突尼斯陶里维尔渠工程和湖北、广东的小面积灌区中试验应用,但由于经费等实际原因未能推广。无论在何种控制方式下,在实际调控中,都需要根据配水指令调节闸门,直到整个系统达到稳定并按配水指令运行,同时调节闸门的先决条件是通过研究确定流量变化所要求的节制闸门的开度。
对灌溉和输水渠道的数值模拟研究发展较早,无论是理论基础还是数值离散格式都相对比较成熟,美国ASCE灌溉渠道水力模拟专门委员会通过对不同离散格式的分析与比较[1],指出用特征线法编程(Amorocho和Strelkoff 1965)实现单一渠道的非恒定流模拟简单易行。Preismann 4点差分隐格式(Liggett和Cunge 1975)也较为常用,这种差分方法计算效果很好,但在各渠道交叉相接时,用该格式离散形成的系数矩阵是不规则、不对称的稀疏矩阵,即无效零元素占了绝大多数,降低了运算速度,使其实用性大打折扣。本文选取冯家山水库灌区总干槐园节制闸至张谢节制闸之间的渠段进行模拟计算,针对梯形单一渠道,按照上游常水深运行方式和下游常水深运行方式,在一定初始条件下和不同闸门调控方式下,对模型渠段的非恒定流过渡进行模拟,比较2种运行方式以预报出各级节制闸调闸时间提前量,保证渠道运行安全,合理调配水量。
1 明渠非恒定流的数学模型
1.1 控制方程
输水渠道任一渠段以节制闸为上下游边界,取水口设在紧邻节制闸的上游边,选择沿渠各点的水位(Z)、流量(Q)作为渠道运行的状态变量,忽略旁侧出流(q)的影响,则任一渠段运行控制方程都可用一维非恒定流Saint-Venant基本方程表述:

式中:Z为水位(m);B为对应水位Z时的过水断面水面宽度(m);Q为流量(m3/s);q为旁侧单宽入流量(m3/(s·m));A为过水断面面积(m2);g为重力加速度(m/s2);i为渠道底坡;C为谢才系数(m1/2);R为水力半径(m);s为流程(m);t为时间(s)。
1.2 方程离散
本文采用矩形网格法对求解域进行划分,把微分方程的连续问题离散化,用数值积分来逼近微分方程,建立网格函数的代数方程组,在离散点上求解网格函数的值[2]。
先将方程化为常微分方程,即顺、逆特征方程

离散上述方程,求Saint-Venant方程组的离散解,即求ω+和ω-的交点P,把待求解区域的距离-时间平面划分成矩形网格,网格的交点称为节点,用i表示距离的分段序号,j表示时间的分段序号。本文研究重点在于水位和流量的过渡过程,因此采用柯朗格式得到时刻P的水位(ZP)和流量(QP)的矩形网格特征线法计算公式。
1.3 边界条件
外边界条件,即入流、出流边界,给定随时间变化的流量Q(t)或者水位Z(t)过程。边界方程形式决定于边界控制条件。
内边界条件,即堰、闸等水头突变处的关系条件。本文主要对闸门的出流流态和流量系数的处理,方法主要应用Swamee根据Henry绘制的过闸流量系数的试验曲线拟合出平板闸门过流的流量系数函数式,其详细处理方法可参见文献[3]。
动态边界和明渠水流同时变化且相互影响,为一耦连问题,若直接求解将使非恒定流问题更加复杂[4]。因而,有必要将系统解耦,使二者互为边界条件,在各个时段上独立求解。
本文仅对一个渠段进行模拟研究,如果需要实现线性多段渠道水力响应过程的连续模拟,对于典型的闸门过流渠段,如图1所示,在Gn+1与Gn+1需
100要满足水流连续条件,即节制闸前断面的流量等于节制闸后断面的流量,可得到(5)式
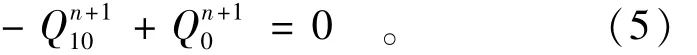
式中:变量Q的上标n+1表示第n+1段上的节制闸号;变量Q的下标数字表示此渠段上的第几断面号。
2 典型模拟渠段
模拟渠段N长l=7 522.0 m,渠道底坡i=1/7 000,糙率由恒定流实测流量水深资料计算取平均值n=0.015,渠段上下游端平板闸门宽度均为bg=4.0 m。渠段断面为梯形,边坡系数m=3,底宽b=5.0 m。初始条件时渠段流量为12m3/s,渠段沿程无流量分出和汇入,通过对恒定非均匀流的水面线计算可得渠段中各个过水断面的初始水深值。
将该模拟渠段N分成11个结点共10个计算单元,其中渠段N上游闸门和下游闸门分别位于其第0断面和第10断面,非均匀流水面线在上游闸门后(结点0)水深为2.673 m,在下游闸门前(结点10)水深为3.6 m。
采用模拟工况:2种运行方式下,渠段引水流量在调节持续时间20 min内,分别减小流量调控,流量调控ΔQ为-1.5,-3.5,-6.0 m3/s后维持不变,渠段边界处的流量调节是假定该流量增减量在调闸过程中随时间作线性变化,按上游常水深运行时,调控渠段下游端闸门,按下游常水深运行时,调控渠段上游端闸门。

图1 典型模拟渠段示意图Fig.1 Typically sim ulated canal stretch
3 计算结果分析
3.1 不同运行方式下的闸门调控过程分析
渠道从水源取水,沿程通过一系列的分水口将所需水量输送到各用水单位。在渠道的运行过程中由于分水等各种因素的干扰,取水口处的水深经常上下波动,通常在分水口处修建节制闸来维持取水口的水深不变,于是一条输水总干渠被各节制闸分成一连串的渠池,构成渠道运行系统,调整取水流量则取水口分水流量以及下游各渠池流量将发生变化,各节制闸门的开度会做出相应的调整,整个渠道系统将产生波动,这种波动能否在一定时间达到稳定是渠道运行的稳定性问题。
按上游常水深运行时,对下游边界流量减小调控,相当于下游N+1渠段完成输配水任务,而N渠段分水闸仍在工作且分水流量稳定不变,或者分水闸完成配水任务关闭,而节制闸Gn+1向N+1渠段输送的流量Qn+1稳定不变[2]。同理,所选渠段按下游常水深运行时,上游边界流量增加相当于节制闸Gn的一个接水过程,上游边界流量减小相当于节制闸Gn的一个送水的过程。在两种运行方式下,都可从模拟结果中分析节制闸Gn+1前为保持闸前稳定水位及流量所应控制的过渡过程及过渡持续时间。
在渠道运行过程中需要按照调控要求得出相应的调闸措施(包括闸门开度和调闸时间)。在2种运行方式下,通过对模拟结果拟合,20min内闸门开度变化过程可以按线性函数拟合如表1。因为一般机械闸门或者手动闸门的调节可表示为开度变化量G0随时间t变化的线性函数[4],为了反映闸门在整个模拟时段内(0~400 min)开度随时间的变化过程,做出模拟曲线如图2、图3所示。随着流量调控和水深经历一段时间趋于稳定,闸门开度的调节也趋于定值。在调节时段(t=20 min)外,闸门开度随时间还有小幅波动,这种波动随时间逐渐减弱,但这种开度的小幅波动在实际的调闸中一般不会出现。因此闸门最终开度,可将流量稳定时闸门开度值作为最终开度。

表1 闸门开度调节函数表Tab le 1 The regu lative function of a gate opening

图2 上游常水深、下游流量线性减小时渠段下游闸门开度调节过程Fig.2 Variation graphs of downstream gate opening under constant upstream water depth and downstream discharge decreased in linear mode
3.2 不同运行方式下各节制闸前后断面水位及流量变化分析

图3 下游常水深、上游流量线性减小时渠段上游闸门开度调节过程Fig.3 Variation graphs of upstream gate opening under constant downstream water depth and upstream discharge decreased in linear mode

图4 上游常水深、下游流量线性减小时渠段上游流量过渡过程Fig.4 Variation graphs of upstream discharge under constant upstream water depth and downstream discharge decreased in linear mode

图5 上游常水深、下游流量线性减小时渠段下游水深过渡过程Fig.5 Variation graphs of downstream depth under constant upstream water depth and downstream discharge decreased in linear mode

图6 下游常水深、上游流量线性减小时渠段下游流量过渡过程Fig.6 Variation graphs of downstream discharge under constant downstream water depth and upstream discharge decreased in linear mode
根据模拟结果分析模拟条件下主要水力要素的变化过程:上游常水深运行方式下,主要对上游流量过渡过程和下游水位过渡过程进行模拟;在下游常水深运行方式下,主要对下游流量过渡过程和上游水位过渡过程进行模拟。2种运行方式下的流量过程线和水位过程线(图4至图7)显示水流过渡过程是一种单向平稳过渡。同一运行方式,在闸门调控的不同流量变幅下,对渠道水位和流量的响应时间以及水流波动幅度影响很大。过渡持续时间随流量变幅的增加而有所延长,波动的幅度也有所增长。以上游常水深运行方式为例,流量变幅为-1.5 m3/s时,流量过渡持续时间仅为229min,当流量变幅增长到-6.0 m3/s时,则过渡时间需要344 min,但波动过程随调控时间的衰减最终都能趋于稳定。如图5所示在上游常水深运行方式下,由于闸门Gn+1开度不同程度的减小,节制闸Gn+1前壅水,因此闸前水位最终都出现了不同幅度的上涨,且随闸门开度减小幅度越大,闸前水位上涨幅度越大;在流量变幅为-6.0 m3/s,过渡时间t=289 min时,趋于平稳的最终水深可达到3.723 m。而在下游常水深运行方式下,恰恰相反,由于节制闸Gn开度不同程度的减小,闸后水面线下降,因此闸后水位最终都出现了不同幅度的下降,且闸门开度减小幅度越大,闸前水位下降幅度越大,最后趋于定值。由此看出,若渠道中水流已经达到另一恒定状态,闸门调控渠段流量只对过渡过程延续时间以及水流波动幅度产生影响,而不影响流量和水位的过渡趋势。2种运行方式下随闸门开度变化幅度的影响,水流恢复稳定状态的时间也有所差异,有利取水口的位置一般在闸前,为使分水的流量保持稳定,需要确定渠段下游流量及水深稳定的时间。根据模拟结果显示:上游常水深运行方式下,下游水深过渡时间在流量变幅为-1.5 m3/s时为229 min,在流量变幅为-3.5 m3/s时为287 min,在流量变幅为-6.0 m3/s时为289 min;下游常水深运行方式下,下游流量过渡时间在流量变幅为-1.5m3/s时过渡时间为230 min,在流量变幅为-3.5 m3/s时为314 min,在流量变幅为-6.0 m3/s时为371 min。由于模型渠段不同闸门调控方式所引起的非恒定流过渡时间以及波动幅度有所差异,所以需要参考模拟结果调控各级闸门。
在闸门调节完毕时,该闸门处断面的流量及水位变化曲线都会出现转折点,在该转折点以后曲线的变化形状或者按原来相反的趋势变化,或者仍按原趋势变化但变化的速率减慢。这是因为,在转折点以前的流量及水位变化由闸门条件产生的干扰波所引起[5],在闸门调节完毕后,水位及流量的变化主要靠渠道自身的调节来稳定目标过渡。而且一般是闸门调节速度越大,曲线变化也越明显。
3.3 同一运行方式下的流量系数过渡过程分析
在不同工况下水流模型不仅能够描述各种流态,而且还需要能描述因水位流量变化而引起的流态转化过程,从而增加了水流模拟的难度。相应于不同工况,闸下过流会出现闸孔自由出流、闸孔淹没出流,本文考虑闸门处流量系数Cd由于受闸门开度G0、闸门上下游水深等因素影响是实时变化的,因而Cd并不是一定值。从图8模拟结果为上游常水深运行流量系数过渡过程,在流量调控时段内,流量系数Cd基本呈线性规律变化,在流量调节时段外,流量系数Cd仍有波动,且流量变幅越大,流量系数Cd的变化越强烈;随着闸门Gn+1上游段水深趋于稳定,流量系数Cd变化也逐渐减弱,最后该系数处于一个稳定值。模拟初始Gn+1闸门下游水深hd=2.64 m,闸门开度G0=0.9 m。按照Swamee提出的判别闸孔出流状态的经验式,计算可知初始时闸孔出流为淹没出流,即闸门开度为最大时是淹没出流,在闸门调控减小的过程中其开度几乎呈直线变化;故在闸门开度减小过程中均为淹没出流,整个过渡过程未出现流态的过渡。

图7 下游常水深、上游流量线性减小时渠段上游水深过渡过程Fig.7 Variation graphs of upstream depth under constant downstream water depth and upstream discharge decreased in linear mode

图8 上游常水深、下游流量线性减小时渠段下游流量系数变化过程Fig.8 Variation graphs of downstream gate discharge coefficient under constant upstream water depth and downstream discharge decreased in linear mode
4 结 论
本文对灌区常用的2种渠道运行方式在闸门调控过程下的明渠非恒定流过渡过程进行研究,数值模拟结果表明:
(1)比较2种运行方式,在上游常水深运行方式下,其优点是能够较快对支渠和下游渠道不可预见的流量增大需求作出反应,而当下游渠道需水量小时又可容蓄水量,适用于供给型渠道。下游常水深运行方式可以使得分水闸能够按照渠中最大的且相对稳定的水深设计,也避免了因水位太低或水面波动给用户带来的配水问题,适用于需求型渠道。从模拟结果来看,同一工况,不同运行方式下,各水力要素过渡时间几乎相同,因此可按灌溉渠道实际需要选择不同的运行方式。
(2)针对闸门不同线性调节方式下,对渠段中研究断面的水力要素的过渡过程进行模拟并给出过渡时间,有利于预报各级节制闸调闸时间提前量,保证渠道运行安全,合理调配水量。
(3)在同一运行方式下,闸门调控的不同流量变幅,对渠道流量的响应时间,以及水流波动幅度影响很大。相同时间内,闸门调控流量变幅越大,流量及水位的变率也越大,水位也越早出现波动情况,对渠道的衬砌安全也越不利。且随调控流量变幅增大渠道的响应时间也会增长,但最终都能过渡到平衡状态。从渠道安全调度运行出发,工程建成后调度配水过程中,在兼顾配水灵活性及缩小配水响应时间的同时,应参考模型程序选择合适的闸门调节时间,调节过闸流量过程。
本文建立的渠系水流调控模型程序简单,应用方便,能全面地反映系统的动态并对其运行作出预测,可得到较明确的闸门调节过程。通过对多种方案的模拟可得到系统最佳运行状态,这对灌区配水管理和工程管理有参考价值。
[1] The ASCE Task Committee on Irrigation Canal System Hydraulic Modeling.Unsteady Flow Modeling of Irriga-tion Canals[J].Journal of Irrigation and Drainage Engi-neering,1993,199(4):515-630.
[2] 吕宏兴,宋松柏,马孝义,等.灌溉渠道闸门调控过程中的非恒定流研究[J].农业工程学报,2002,18(6):18-22.(LV Hong-xing,SONG Song-bai,MA Xiao-yi,etal.Unsteady Flow During Regulating Gate in Irrigation Canal[J].Transactions of the CSAE,2002,18(6):18-22.(in Chinese))
[3] Prabhata K S.Sluice-gate discharge equations[J].Jour-nal of Irrigation and Drainage Engineering,ASCE,1992,118(1):56-60.
[4] 余国安.闸门调控下的灌溉渠道非恒定流数值模拟研究[D].陕西杨凌:西北农林科技大学水利与建筑工程学院,2004.(Yu Guo-an.Numerical simulation of sluice gate regulated unsteady flow in irrigation canals[D].Shaanxi Yangling:Northwest A&FUniversity Agri-cultural Soil&Water Engineering,2004.(in Chinese))
[5] 丁志良,谈广明.输水渠道中闸门调节速度与水面线变化研究[J].南水北调与水利科技,2005,3(6):46-50.(DING Zhi-liang,TAN Guang-ming.Study of sluice gate regulating speed and changes ofwater-surface Profile in transportation channels[J].South-North Water Transfers and Water Science&Technology,2005,3(6):46-50.(in Chinese))
[6] 王长德,韦直林,张礼卫.上游常水位自动控制渠道明渠非恒定流动态边界条件[J].水利学报,1995,2
(2):46-57.(WANG Chang-de,WEIZhi-lin,ZHANG Li-wei.Dynamic boundary condition of unsteady flow in open canalwith automatic constantupstream level control[J].Journal of Hydraulic Engineering,1995,2(2):46-57.(in Chinese))
(编辑:王 慰)
Numerical Simulation of Unsteady Flow in Irrigation Canals w ith Two Operating M odes
HAN Yu1,LV Hong-xing1,YU Guo-an2
(1.College ofWater Resources and Architectural Engineering,Northwest A&F University,Yangling 712100,China;2.Institute of Geographic Sciences and Natural Resources Research,CAS,Beijing 100101,China)
To research unsteady flow transition process in a single irrigation canal stretch for the purpose of ensuring the safe operation of irrigation canals and rational allocation of water,we consider adopting different operating modes,aswell as different gate regulationmodes etc.,under the two operation conditions of constant upstream wa-ter depth and constant downstream water depth,conduct the canal unsteady flow numerical simulation with the rec-tangular grid characteristic method in the trapezoidal cross-section under the different gate controls,and compare the results of two operatingmodes and forecast time in advance to control the sluice atall levels.So,the results can fully reflect the dynamic and more precise adjustment process.
constant upstream water depth operation;constant downstream water depth operation;gate regulation;open-canal unsteady flow;numerical simulation
TV133.2
A
1001-5485(2010)03-0029-05
2009-02-01;
2009-03-09
十一五国家科技支撑计划(2006BAD11B04)
韩 宇(1985-),女,黑龙江大庆人,硕士,主要从事灌溉水力学方面的研究,(电话)15249222459(电子信箱)anqi0594@163.com。
吕宏兴(1955-),男,陕西陇县人,教授,博士生导师,主要从事工程水力学、节水灌溉新技术及灌区现代化管理方面的研究,(电话)13991333552(电子信箱)lvhongxing@tom.com。
