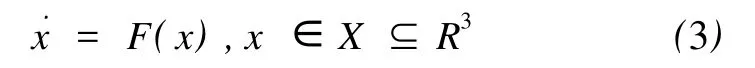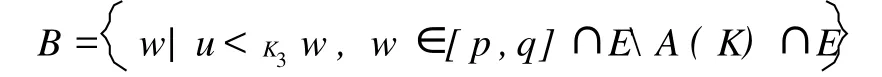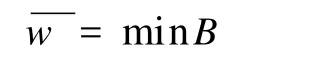关于交错锥的三维合作系统平衡点存在性问题
2010-09-04潘根安
潘根安, 肖 箭
(1.合肥师范学院数学系,安徽合肥230061;2.安徽大学计算科学学院,安徽合肥230039)
关于交错锥的三维合作系统平衡点存在性问题
潘根安1, 肖 箭2
(1.合肥师范学院数学系,安徽合肥230061;2.安徽大学计算科学学院,安徽合肥230039)
研究关于交错锥的三维合作系统平衡点存在性问题,得到定理1:设 f是D上一个连续可微的 K3型合作向量场,其中 D是 P3凸的。若 K为系统˙x=F(x),x∈X⊆R3的闭轨道,则有:(a)系统(3)一定存在两平衡点 p,q,使得 p
竞争系统;合作系统;平衡点;流形;K3锥
1 引言
通过对合作系统和竞争系统的研究,知道解映射保持 R3+(R3-)产生的,因此考虑除 R3+及 R3-以外的其他的锥,可以扩大三维合作系统的研究范围。1952年L.P.Burton和U.M.Whyburn引入锥
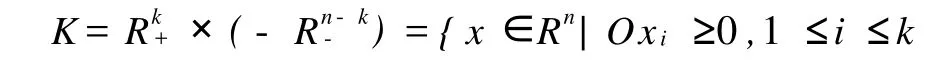
且xj≤0,k+1≤j≤n},
显然当k=n时

当k=0时
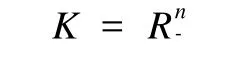
Smith在文[1]中考虑一般的锥 Km,Km={x∈Rn:(-1)mixi≥0,1≤i≤n},其中 m=(m1,m2,…, mn),mi∈{01}。Km是Rn上的一个锥,其由此产生的偏序为:
x≤my,即 y-x∈Km⇔当 mi=0时,xi≤yi,且当 mi=1时,yi≤xi;x x≺my,即 y-x∈int K⇔当 mi=0时,xi 考虑三维系统的锥 K3,定义偏序: x≤K3y,即 y-x∈K3⇔当 mi=0时,xi≤yi,且当 mi=1时,yi≤xi; x x≺K3y,即 y-x∈int K⇔当 mi=0时, xi< yi,且当 mi=1时,yi 记 P为一个对角矩阵,且 P=diag{(-1)m1, (-1)m2,…,(-1)mn},易知 P=P-1,则有 x 定义1 若∀x,y∈D⊂R3,0 定义2 考虑方程 其中f是D⊂R3上连续可微向量场,D为 P3凸的。若(-1)mi+mj≥0,i≠j,x∈D,则称(1)是K3锥的合作系统,或称(1)为 K3型合作系统。若(-1)mi+mj≤0,i≠j,x∈D,则称(1)是关于 K3锥的竞争系统,或称为 K3型竞争系统。 注:这里给出一种判断在区域 D(D是 P3凸的)上的系统是 K3型合作系统还是 K3型竞争系统的方法。 命题1 在 K3锥上的合作系统(1)中用 证明 因为D是P3凸的,所以 PD是P3凸的,其中 令 再令 显然 故有 其中 由同序性可知 命题2 考虑系统(1)及其对应的系统(2),可知: (1)若ω(x)是系统(1)的极限集,则ω(y)是系统(2)的极限集,其中 y=Px,且ω(x)=Pω(y); (2)若u是系统(1)的平衡点,则 Pu是系统(2)的平衡点。 因为 所以 (2)由 u是系统(1)的平衡点知道:对∀t>0,有φt(u)=u。所以 故 Pu是系统(2)的平衡点。 命题3 考虑系统 设 F:X→R3是一个C1的 K3型合作向量场。假设如下条件成立: (a)X=R3,或intR3+,或[[p,q]]K3; (b)X中每个正半轨有紧闭包; 则有: (1)ω(x)中不能存在两点 u,v,满足 u≺K3v; (2)存在 T>0,满足 x(T)K3≥x(0)或 x(T)≤K3x(0),则ω(x)为一闭轨线,且周期为 T; (3)若y∈ω(x),且 x 考虑 K3型合作系统,基于文[7]中定理的相应的条件,亦能得到相同的结果,主要考虑三维交错锥合作系统的平衡点,目的把文[7]的一些结果推广到交错锥上进行研究和探讨。 引理1[7]设 x∈X且 p0,q0分别为周期轨道K的下确界和上确界,则有ω(p0)={p},ω(q0)= {q}并且满足 p≤K3p0≤K3K≤K3q0≤K3q且 p 引理2[7]设在[p,q]中所有平衡点都是单点集,p和q是两个平衡点且按照上面的方式定义,则[[p,q]]包含一系列的平衡点且它们的指标之和为+1。 定理1 设f是D上一个连续可微的 K3型合作向量场,其中D是P3凸的。若 K为系统 的闭轨道,则有: (a)系统(3)一定存在两平衡点 p,q,使得 p (b)开序区间[[p,q]]K3中一定存在一个平衡点u,使得它在序关系 (c)集合 A(K)一定存在一个不稳定的平衡点v。 证明 证明(a)由引理1知系统(3)确实存在两个平衡点 p,q,有 p (b)记a=p和b=q,显然 K⊂[[p,q]]K3和 A (K)⊂[[p,q]]K3,因此知开序区间[[p,q]]中存在一个平衡点 u,满足它在关系 (c)仅证明集合A(K)含有有限个平衡点情形,其余情形类似。以下分两种情况讨论: 首先,假设存在两点 u,v∈A(K)∩E满足u≤K3v以及区间[u,v]K3不含有其它任何平衡点。则由引理2知有 u 其次,假设集合A(K)中任何两个不相同的点在关系≤K3下不相关。现给定点 u∈A(K)∩E,我们定义 易知集合B为非空、有下界的。于是再定义 [1] Smith.H.L.Periodic orbits of competitive and cooperative system[J].J.Differential Equations,1986,65:361-373. [2] Taká èP.Convergence to equilibrium on invariantd-hypersurfaces for strongly increasing discrete-time semigroups[J].J. Math.Anal.Appl,1990,148:223-244. [3] Dancer E N and Hess P.Stability of fixed points for orderpreserving discrete-time dynamic system[J].J.Reine Angew. Math,1991,419:125-139. [4] M.W.Hirsch.Systems of differential equations that are competitive or cooperative V:Convergence in 3-dimensional systems[J].J.Differential Equations,1989,80:94-106. [5] 肖箭.关于具有不变函数的自治系统周期的几个问题[J].安徽大学学报,1999,3:5-8. [6] 肖箭,黄顺林.关于Hirsch和Jiang的全局稳定性定理的注记[J].安徽大学学报,2002(4):1-4. [7] 潘根安,肖箭.关于三维不可约合作系统的平衡点与周期轨道[J].安徽大学学报,2006.3:14-16. Equilibrium Points of Three-dimensional Cooperative Systems on Staggered Cone PAN Gen-an1, XIAO Jian2 (1.Department of Mathematics,Hef ei Normal University,Hef ei230061,China; 2.School of Computer Science,A nhui University,Hef ei230039,China) In this paper,we study the existent problem of three-dimensional cooperation system’s equilibrium point on staggered cone.Then the theorem 1:is obtained:letfbe a continued differentiable vector K3field onD,which isP3convex.IfKis a closed orbit of system(3),one can obtain the resnlts as follows:(a)there exists two pointsp,q∈Esuch thatp competitive system;cooperative system;equilibrium;manifold;cone ofK3 O175 A 1674-2273(2010)06-0004-03 2010-03-08 安徽省高校自然科学基金(KJ2010B165);合肥师范学院重点项目(2010 kj04zd) 潘根安(1976-),男,安徽省寿县人,硕士,合肥师范学院数学系教师;研究方向:微分方程定性理论;肖箭(1963-),男,安徽合肥人,硕士生导师,安徽大学计算科学学院,教授。研究方向:微分方程定性理论。
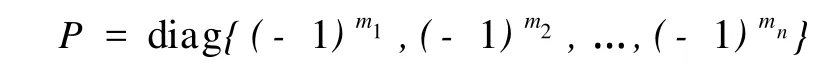
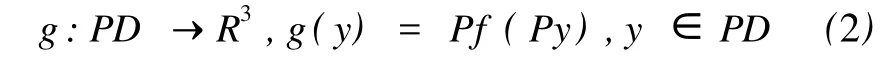

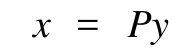
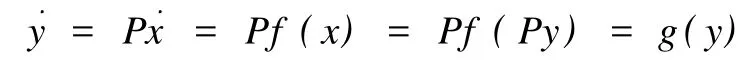
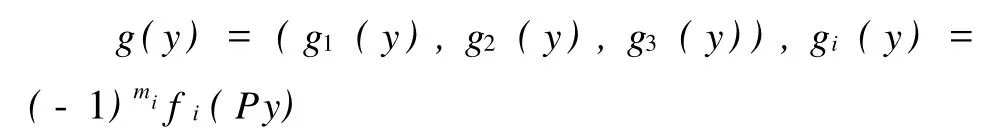
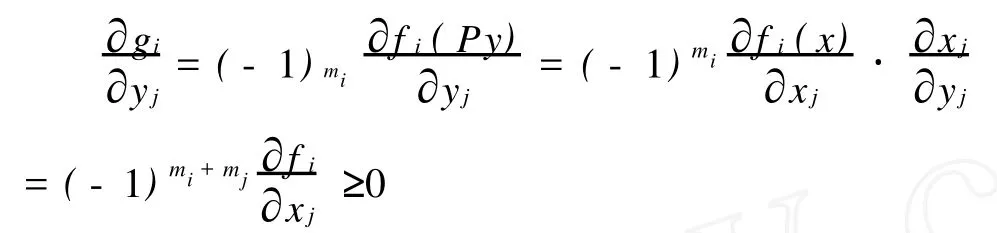
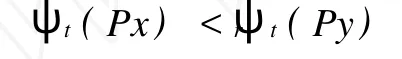
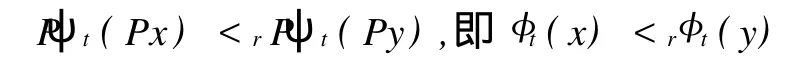
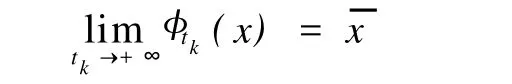
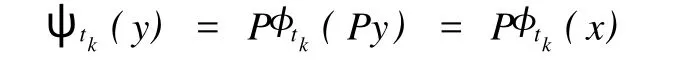
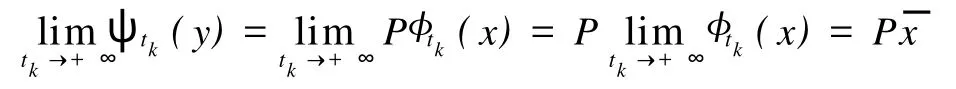
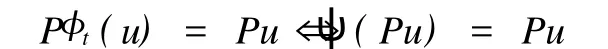

2 K3型合作系统的平衡点问题