活性粉末混凝土连续梁塑性性能试验

李 莉，郑文忠

(哈尔滨工业大学 土木工程学院，哈尔滨150090，lily－tcl@163.com)

活性粉末混凝土(RPC)是一种具有超高强度、超高韧性、超高耐久性等优良性能的新型混凝土材料［1－2］.目前，国内外对 RPC 的材料、配比、养护条件、耐久性和强度等进行了大量的试验研究［3－5］.在国外的某些试点工程中也有所应用［6－7］.实际工程中多数构件为超静定结构，对于普通钢筋混凝土连续梁的塑性设计方法已做过大量研究［8-10］，由于RPC的力学性能指标与普通混凝土有较大不同，使得钢筋RPC连续梁塑性铰的形成、发展以及塑性设计与普通钢筋混凝土连续梁不同，本文制备了5根钢筋RPC两跨连续梁的试件，进行了单跨单点加载试验，考察了试验梁的塑性铰发展过程，提出了钢筋RPC连续梁在两个承载能力极限状态下的等效塑性铰区长度计算公式，和以中支座附近相对塑性转角为自变量和以中支座相对受压区高度为自变量的弯矩调幅系数计算公式.

1 试验概况

1.1 试验原材料

试验梁RPC选用哈尔滨亚泰牌P.O42.5硅酸盐水泥;SiO2含量85.72%，比表面积24200m2/kg的唐山硅灰;鞍山钢铁公司生产的比表面积为4200cm2/g的S75型矿渣粉;山东莱芜汶河化工有限公司的FDN浓缩型高效减水剂;哈尔滨晶华水处理材料有限公司生产的40～70目和70～140目石英砂;直径为0.22mm，长径比为59.1的鞍山昌宏钢纤维厂生产的平直钢纤维.纵筋采用HRB235和HRB400钢筋，箍筋采用HRB335钢筋.

1.2 试验用RPC配合比

根据前期配合比试验优选了一组强度较高，流动度较好的配合比，如表1所示［2］.

表1 试验用RPC配合比

1.3 材料性能

为了得到本批试验所使用的RPC材料力学性能，分别进行了轴压和轴拉力学性能试验.实测的RPC棱柱体强度为102.28MPa，峰值应力对应的应变为3560×10-6，极限压应变为5500×10-6，弹性模量为41237MPa.试验中所用的一级钢筋屈服强度为275.0MPa，极限强度为310.5MPa，屈服应变为1310×10-6;三级钢筋的屈服强度平均值为475.7MPa，极限强度平均值为618.3MPa，屈服应变平均值为2378.3×10-6.

1.4 试验梁参数

混凝土连续梁塑性设计的关键参数为中支座控制截面的弯矩调幅系数.因此以调幅系数为变化参数设计了5根RPC连续梁试件，参数见表2.

1.5 加载方案

采用液压千斤顶分别在试验梁两跨中点单点对称施加集中荷载，试验梁中支座为固定铰支座，两边支座为滚动铰支座.试验装置如图2所示.为确保试验梁在试验过程中与真实受力状态一致，通过图2所示的中支座控制截面下的100 t螺旋式千斤顶反复调节中支座高度，直至试验梁在自重及加载设备作用下，3个支座反力实测值与按两跨连续梁计算简图得到的支反力弹性计算值的误差在允许范围内.

表2 连续梁试件设计参数

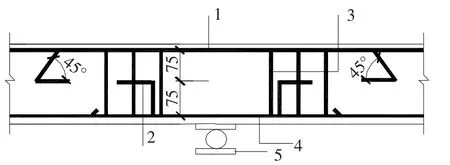
图1 中支座配筋示意图

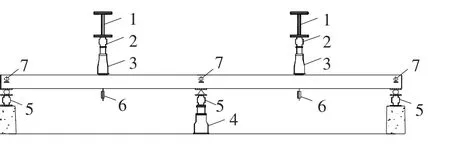
图2 连续梁试验加载设备

梁的挠度通过布置于支座和跨中的位移计测得，裂缝宽度通过读数放大镜测得.中支座和跨中控制截面沿梁高的应变通过布置于梁侧的5个应变引伸计测得.试验加载采用分级加载，直到试件破坏.

2 试验现象及结果

2.1 试验现象

当中支座控制截面受压边缘混凝土达到极限压应变εcu=5500×10-6时为设计用承载能力极限状态，这里称为破坏标志Ⅰ，此时还可继续承担荷载;当试验梁任一跨出现荷载开始减小，变形持续增大时为真实承载能力极限状态，称为破坏标志Ⅱ.

5根试验梁均在中支座附近先出现第一条裂缝，随着荷载的增长，裂缝宽度和数量不断增加，中支座纵向钢筋首先屈服，随着荷载发展逐渐形成塑性铰，由于加载的细微差异和试件材料离散性，试件两跨跨中的裂缝开展和纵向钢筋应变发展略有不同.

2.2 试验结果

2.2.1 试验梁实测开裂弯矩和极限弯矩

根据前期工作提出的RPC梁开裂弯矩计算式得到计算值，与实测值对比如表3所示.

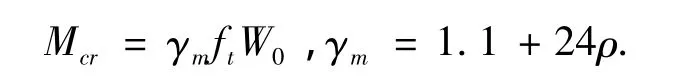
式中:ρ为纵向受拉钢筋截面配筋率，W0为换算截面抵抗矩.

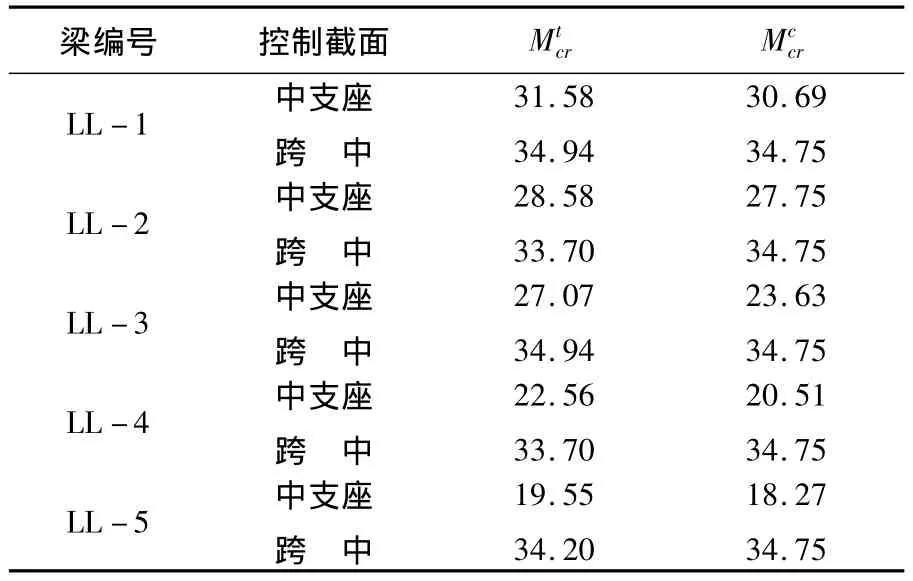
表3 试验梁开裂弯矩计算值与实测值对比 kN·m

令x=Mccr/Mtcr，其平均值=0.99，均方差σx=0.134，变异系数δx=0.018，可见这种开裂弯矩计算方法可用.

试验梁对应于破坏标志Ⅰ荷载值Pu，Ι、边支座反力Ru，Ι及正截面抗弯极限弯矩Mtu，Ι如表4所示.试验梁对应于破坏标志Ⅱ的荷载值Pu，Ⅱ、边支座反力Ru，Ⅱ及正截面抗弯极限弯矩Mtu，Ⅱ，如表5所示.可以看出，虽然各试验梁跨中控制截面配置的纵筋相同，但破坏时的承载力不同，随着中支座控制截面配筋的减少，跨中控制截面的承载力增大.

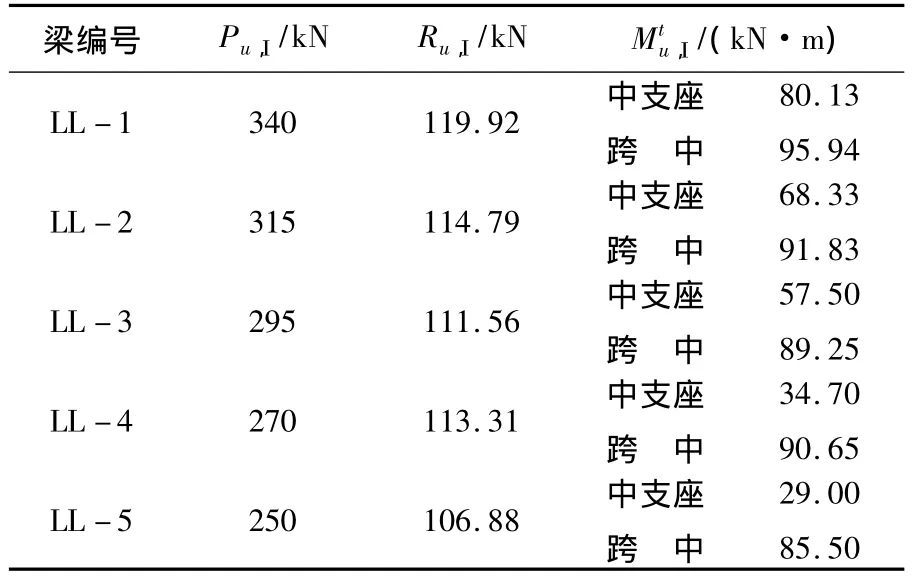
表4 试验梁对应于破坏标志Ⅰ的极限弯矩实测值

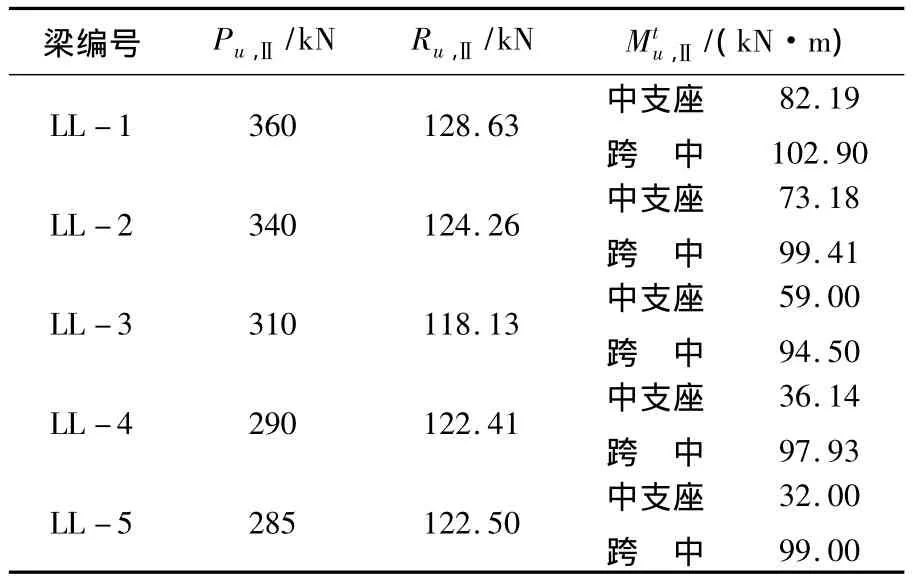
表5 试验梁对应于破坏标志Ⅱ的极限弯矩实测值

2.2.2 试验梁的变形

根据布置在试验梁跨中及各支座的位移计测到的位移实测值，可计算得到在外荷载作用下跨中挠度，各试验梁两跨的荷载－挠度曲线如图3所示，各试验梁均经过了中支座附近开裂、跨中附近开裂、中支座钢筋屈服、跨中钢筋屈服、中支座达到极限压应变和跨中达到极限压应变6个阶段，每个阶段所对应的荷载分别列于图中.开裂前，试验梁的两跨中挠度均很小，且基本相等;由试验梁开裂至中支座控制截面纵向钢筋屈服，跨中挠度开始有较快增长;在中支座及跨中的塑性铰形成及转动过程中，跨中挠度急速增长，占最终变形的绝大部分.

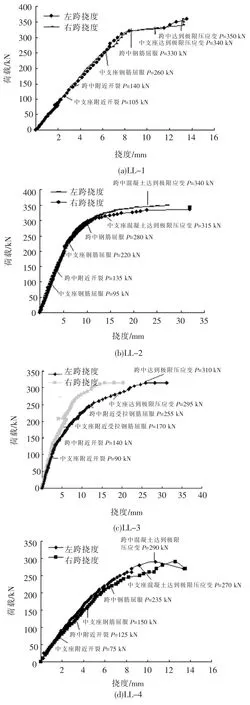
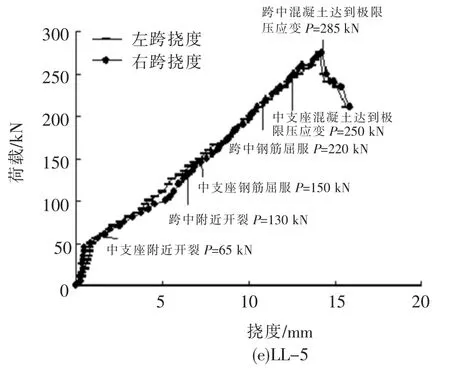
图3 各试验梁荷载－挠度曲线

3 钢筋活性粉末混凝土连续梁的塑性设计

3.1 梁的内力重分布

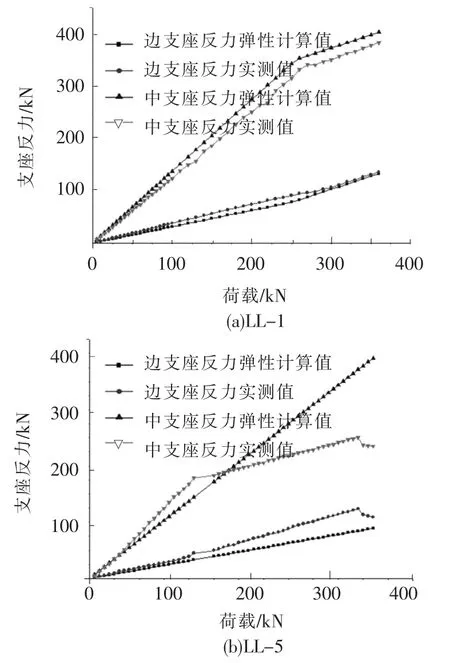
图4 试验梁支座反力弹性计算值与实测值的对比

图4和图5以LL-1和LL－5为例给出了试验梁在加载过程中支座反力和中支座控制截面弯矩的弹性计算值和实测值的对比情况.由图中可以看出，从开始加载之后的若干级荷载作用下，试验梁的支反力实测值与弹性计算值、中支座控制截面弯矩实测值与弹性计算值基本相等，表明此时试验梁处于弹性受力阶段;随着荷载的增加，实测值与弹性计算值开始有偏差，至中支座控制截面纵向钢筋受拉屈服过程中，试验梁边支反力实测值均逐渐较弹性计算值增大、中支座反力实测值逐渐较弹性计算值减小;相应地，中支座控制截面弯矩实测值逐渐小于弯矩弹性计算值、跨中控制截面弯矩实测值逐渐大于弯矩弹性计算值，表明试验梁开始出现一定程度的内力重分布现象.

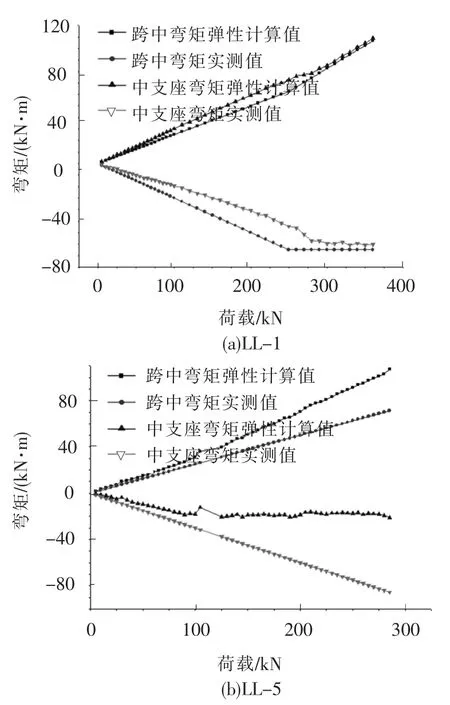
图5 试验梁支座弯矩弹性计算值与实测值的对比

3.2 塑性铰长度及塑性转角

3.2.1 基于设计用承载能力极限状态下

在各试验梁中支座控制截面800mm长范围内的纵向钢筋表面粘贴了间距为25mm的应变片，可测得中支座控制截面两侧纵向钢筋应变不小于屈服应变的长度，即中支座两侧的实际塑性铰区长度.φd为设计用承载能力极限状态下的极限曲率，φy为屈服曲率，以实际塑性铰区内非弹性曲率所包围面积相等为原则，将非弹性曲率等效为矩形分布，由此可确定试验梁在设计用承载能力极限状态下的等效塑性铰区长度.试验梁在达到设计用承载能力极限状态时中支座控制截面附近曲率分布和等效塑性铰区如图6所示.此时塑性铰的转角为θpd=(φd-φy)lpd.基本参数见表6.

取5根试验梁基于设计用承载能力状态时两侧等效塑性铰区长度的平均值，则Lpd=0.40h0.

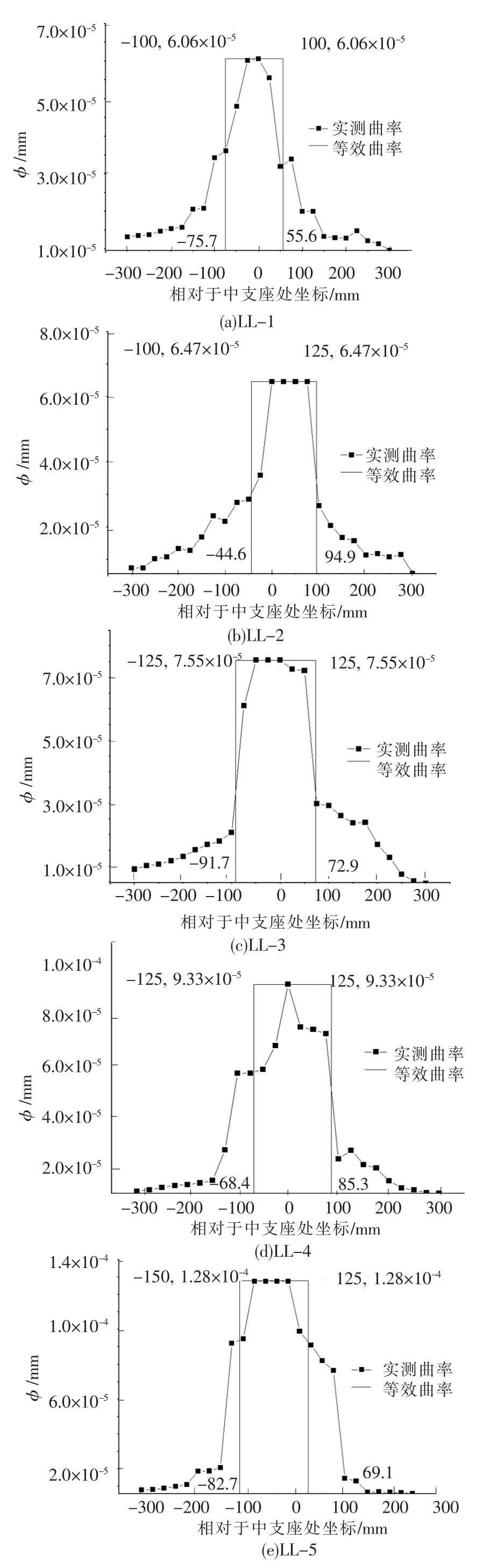
图6 基于设计用承载能力极限状态时试验梁实际塑性铰区内实测曲率及其等效矩形分布

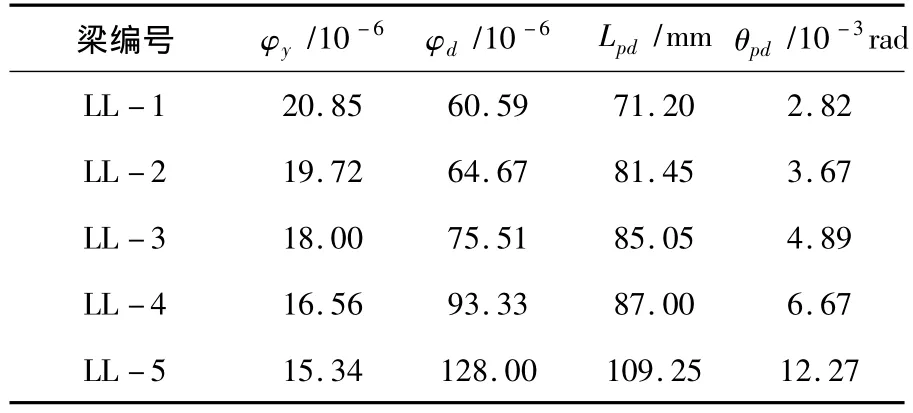
表6 基于设计用承载能力极限状态时试验梁塑性铰区长度和塑性转角

3.2.2 基于真实承载能力极限状态

φu为试验梁真实承载能力状态下极限曲率，按照与实际塑性铰区非弹性曲率所包围面积相等的原则，将曲率等效为矩形分布.从而可得到中支座控制截面两侧等效塑性铰区长度lpu.图7为各试验梁在该状态下实测曲率分布和等效矩形分布，塑性转角为 θpu=(φu- φy)lpu.基本参数见表7.

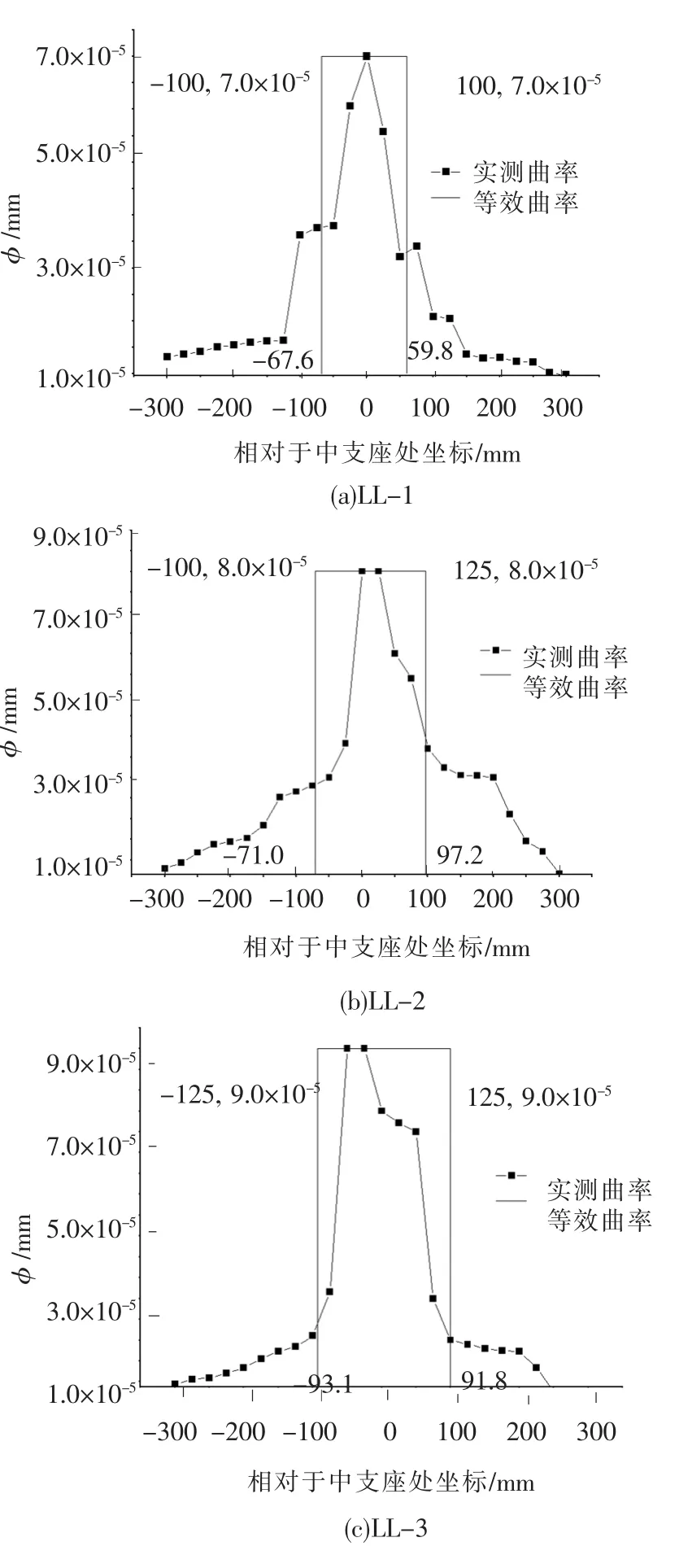
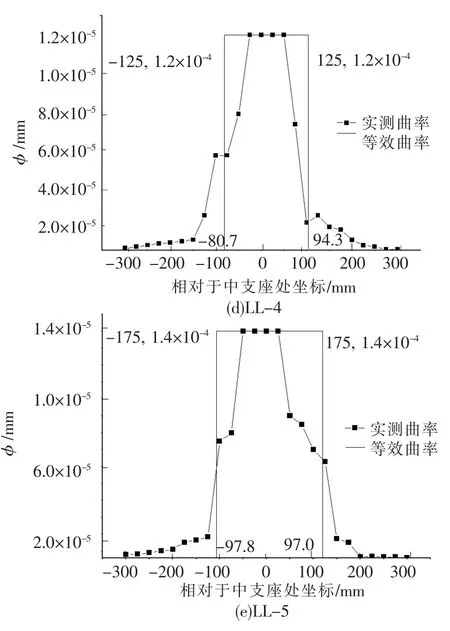
图7 基于真实承载能力极限状态时试验梁实际塑性铰区内实测曲率及其等效矩形分布

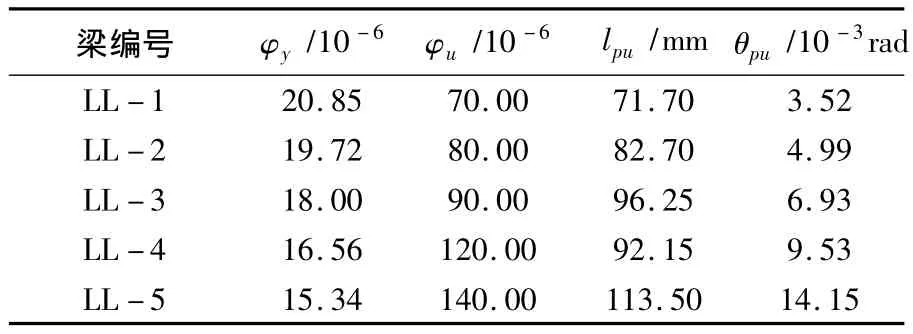
表7 基于真实承载能力极限状态时试验梁塑性铰区长度和塑性转角

取5根试验梁基于真实承载能力状态时两侧等效塑性铰区长度的平均值，则Lpu=0.45 h0.

3.3 塑性调幅系数的计算

3.3.1 基于设计用承载能力状态下的弯矩调幅系数试验梁在设计用承载能力极限状态下中支座弯矩实测值Md，中支座弯矩弹性值Mde和调幅系数βd如表8所示.以βd为纵坐标，以达到该状态时相对塑性转角θpd/h0为横坐标，得到试验梁试验点分布，见图8所示，根据图中数据拟合得到

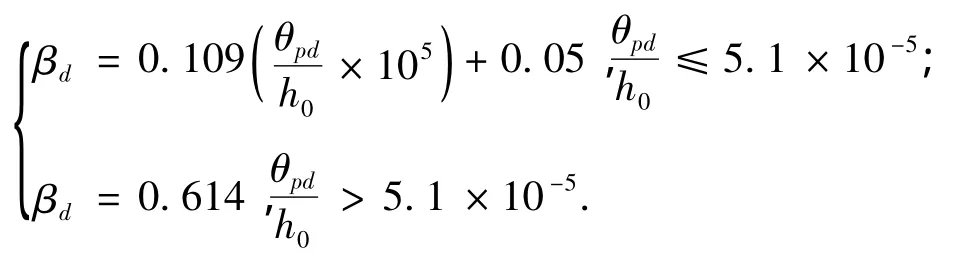
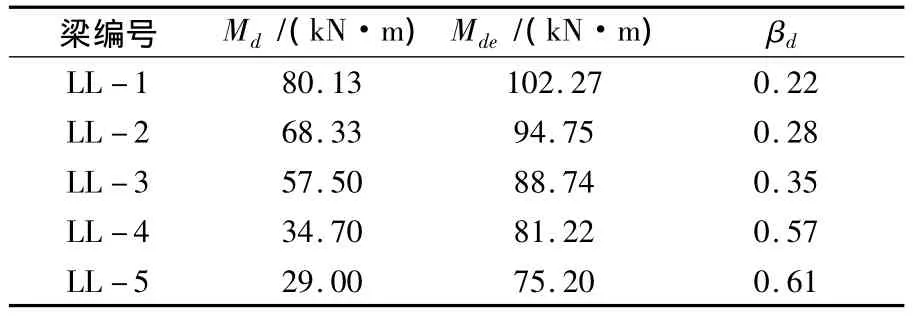
表8 各试验梁在设计用承载能力极限状态下的Md，Mde和βd

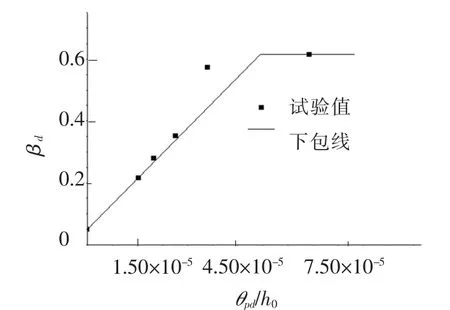
图8 βd与θpd/h0试验点分布及关系曲线

表9列出了根据实测值计算的设计用承载能力状态下的中支座控制截面混凝土相对受压区高度ξi与调幅系数βd的计算值.

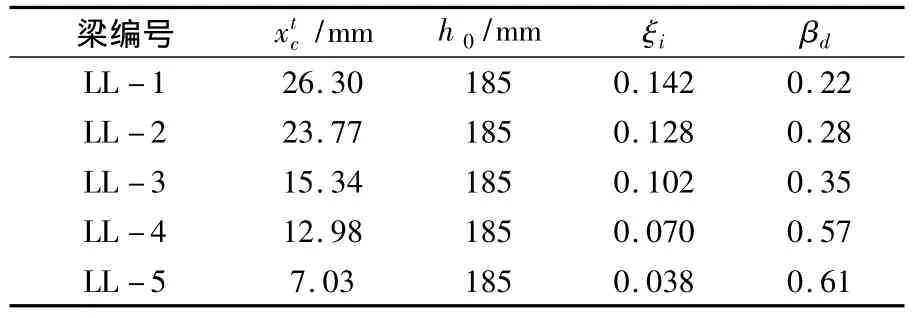
表9 试验梁实测的中支座相对受压区高度ξi及βd

5根钢筋RPC连续梁βd与ξi试验点分布，见图9.由此可得到

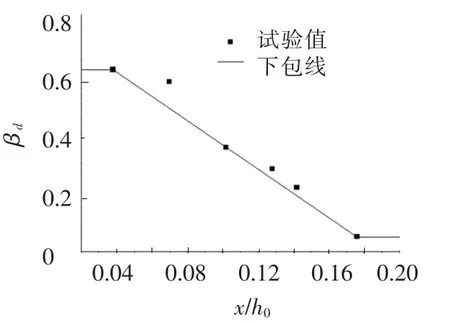
图9 βd与x/h0试验点分布及关系曲线

3.3.2 基于真实承载能力极限状态的弯矩调幅系数试验梁在真实承载能力极限状态下的中支座弯矩实测值Mu，中支座弯矩弹性计算值Mue以及调幅系数βu见表10.以βu为纵坐标，以达到该状态时相对塑性转角θp/h0为横坐标，得到试验梁试验点分布，见图10，根据图中数据拟合得到

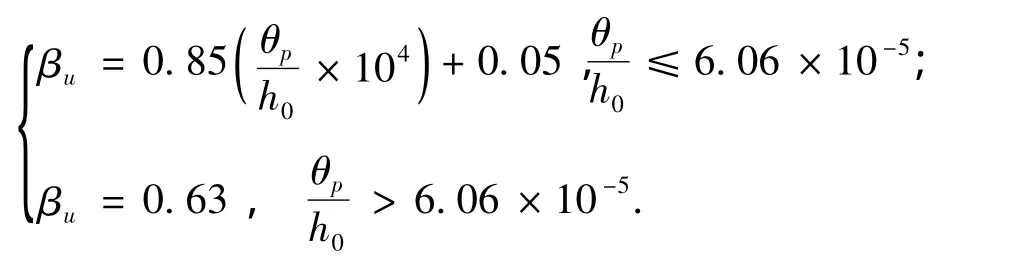
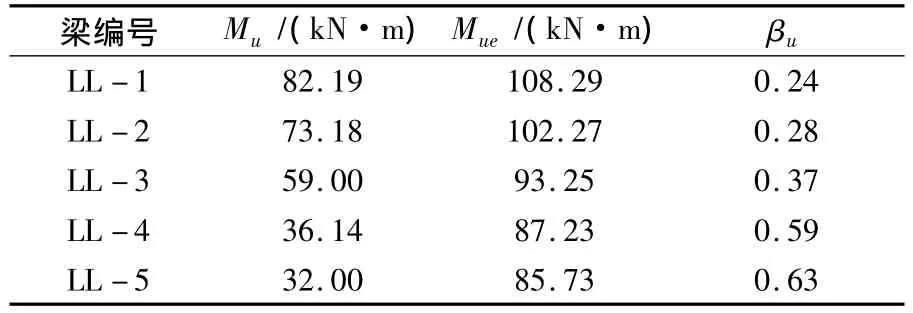
表10 各试验梁在真实承载能力极限状态下的Mu，Mue和βu

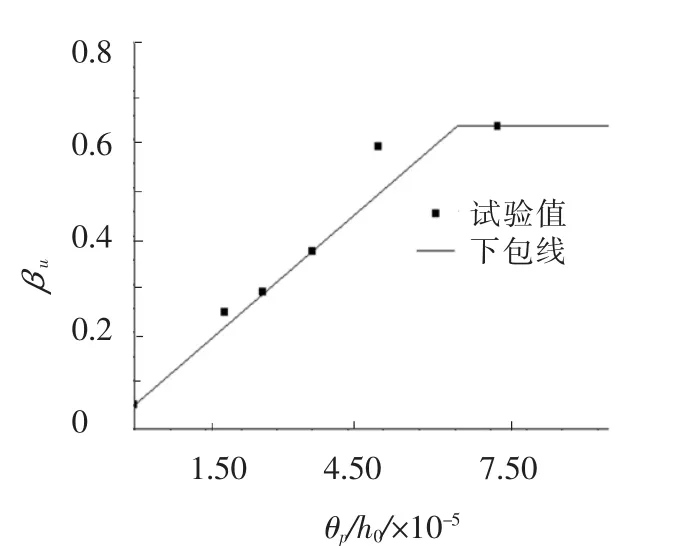
图10 βu与θp/h0试验点分布及关系曲线

表11列出了根据实测值计算的真实承载能力状态下的中支座控制截面混凝土相对受压区高度ξi与调幅系数βu的计算值.5根钢筋RPC连续梁βu与ξi试验点分布，见图11.由此可得到以ξi为自变量的中支座弯矩调幅系数βu为

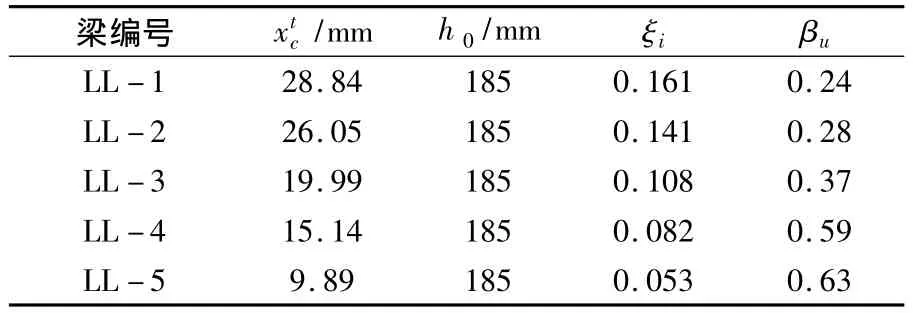
表11 各试验梁在真实承载能力状态下实测的中支座相对受压区高度ξi及调幅系数βu

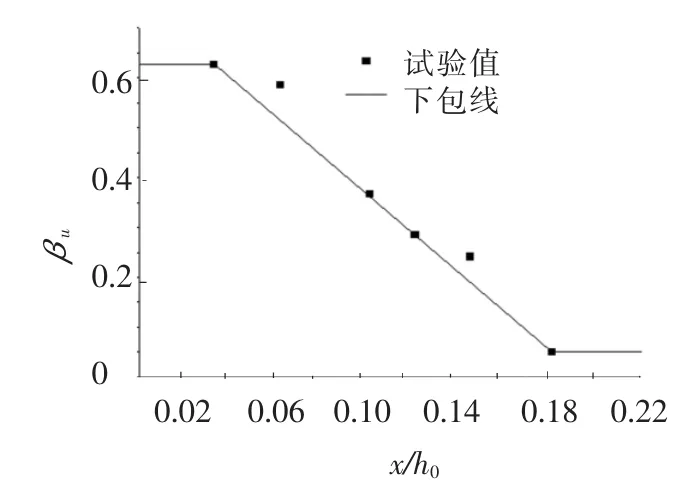
图11 βu与x/h0试验点分布及关系曲线

钢筋RPC连续梁的调幅能力比相同截面相同配筋的普通钢筋混凝土连续梁大，这是由于RPC的极限压应变为5 500×10-6，大于普通混凝土的3 300×10-6，对于适筋梁，截面的极限曲率φu取决于混凝土的极限压应变，而屈服曲率φy取决于钢筋的屈服应变，因此钢筋RPC连续梁的中支座截面极限曲率φu比普通钢筋混凝土连续梁大，使得钢筋RPC连续梁的中支座塑性铰转角比普通钢筋混凝土连续梁大.由此说明钢筋RPC连续梁具有更优越的塑性调幅能力.

4 结论

1)通过5根钢筋活性粉末混凝土两跨连续梁的破坏试验考察了试验梁的开裂、中支座控制截面纵向钢筋屈服，跨中控制截面纵向钢筋屈服和极限破坏状态的受力特征.

2)建立了活性粉末混凝土连续梁达到设计用承载能力极限状态和真实承载能力极限状态时的等效塑性铰区长度计算公式.

3)建立了活性粉末混凝土连续梁达到设计用承载能力极限状态和真实承载能力极限状态的以中支座附近相对塑性转角和以相对受压区高度为自变量的弯矩调幅系数计算公式.

［1］RICHARD P.Reactive powder concrete:a new ultrahigh strength cementitious material［C］//The 4th International Symposion Utilization of High Strength/High Performance Concrete，Paris，France:［s.n.］，1996:1343-1349.

［2］RICHARD P，CHEYREZY M.Composition of reactive powder concretes［J］.Cement and Concrete Research，1995，25(7):1501 -1511.

［3］郑文忠，李莉.活性粉末混凝土配制及其配合比计算方法［J］.湖南大学学报，2009，35(2):13-17.

［4］谢友均，刘宝举，龙广成.掺超细粉煤灰活性粉末混凝土的研究［J］.建筑材料学报，2001，9:280 －284.

［5］ROUX B N，ANDRADEJ C，SANJUAN M A.Experimental study of durabilty of reactive powder concretes［J］.Journal of Materials in Civil Engineering，1996，8(2):1-6.

［6］张燕.活性粉末混凝土在结构工程中的应用及发展［J］.河南建材，2003(4):18－20.

［7］周文元.活性粉末混凝土在道路桥梁工程中的应用［J］.水运工程，2004(12):103 -105.

［8］邓宗才，马俊.钢筋混凝土连续梁塑性分析的试验研究［J］.建筑结构，1997(5):16-18.

［9］杨春峰.无粘结预应力混凝土连续梁截面曲率延性分析与塑性设计［D］.哈尔滨:哈尔滨工业大学，2003.

［10］清华大学土木与环境工程系，山西省建筑科学研究所.钢筋混凝土连续梁弯矩调幅限值的试验研究［J］.山西建筑，1981(1):1－33.