策略集扰动下Nash平衡的精炼

冯冰

（广东岭南职业技术学院博雅教育学院，广东广州510663）

策略集扰动下Nash平衡的精炼

冯冰

（广东岭南职业技术学院博雅教育学院，广东广州510663）

通过定义一种策略集的扰动映射，引入一种新的稳定Nash平衡的概念，并利用Ky Fan不等式定理的相关结果证明该稳定Nash平衡的存在性.

ε－Nash平衡；χ－稳定Nash平衡；扰动；精炼

1 引言及预知识备

为了研究方便，首先给出n人非合作对策的模型：

局中人集合：N＝｛1,…,n｝；

局中人的策略集：∀i∈N，Xi是第i个局中人的策略集，其中X1,…,Xn分别为线性拓扑空间E1,…, En中的子集；

若记对策P所有Nash平衡点的集合为E(f)，由文献[1]中Nash平衡的存在性定理可知，当局中人的支付函数和策略集满足一定条件时，在一个对策P中，Nash平衡点并不是唯一的，也就是说E(f)通常都是非空集合，有时甚至可能是无穷的.满足给定条件所得的Nash平衡，对于给定的具体问题而言有一些并不满足合理性的要求，因此，人们总在试图剔除某些不理想的Nash平衡，也就是对Nash平衡加以精炼，保留一些具有稳定性的解.关于Nash平衡稳定性问题的研究一直是对策论领域的一个热点，国内外学者通过考虑对策略集或支付函数的各种扰动，得到了一系列关于Nash平衡的精炼结果，具体可见文献[2－4].本文中，笔者主要是运用文献[5]中关于Ky Fan点稳定性研究所得的相应结果来讨论Nash平衡的稳定性问题.

为了便于研究，下面先给出一些引理和定义.

引理1（Ky Fan不等式定理）设X为Hausdorff线性拓扑空间E中的非空紧凸集，R为实数集，f：X×X→R满足以下条件：

1）f(x,x)≤0，∀x∈X；

则存在y*∈X，使得f(x,y*)≤0，称引理1中y*为KF点，∀x∈X.

设集值映射T：[0,1]→X，记int(X×X)为X×X的内部，且T满足以下条件：

Ⅰ）T：[0,1]→X是连续的，且∀ε∈[0,1]，T(ε)×T(ε)是X×X的一个非空紧凸子集；

Ⅱ）T(0)×T(0)＝X×X，且当0≤ε＜ε′≤1时，T(ε′)×T(ε′)⊂int T(ε)×T(ε).

又设映射G：T(ε)×T(ε)→R，其中ε∈[0,1]，且满足以下条件：

Ⅲ）G(x,y)＝f(x,y)－ε，(x,y)∈T(ε)×T(ε).

Ⅳ）f(x,y)满足Ky Fan不等式定理中的条件1），2），且对每一固定的是凹的.

定义1[5]称映射对(T,G)是正则的，如果它满足以上的条件Ⅰ），Ⅱ）和Ⅲ），Ⅳ）.

定义2[5]对于以上定义的映射对(T,G)，∀ε∈[0,1)，如果∃y∈T(ε)，使得f(x,y)≤ε，∀x∈T(ε)，则称点y∈T(ε)为函数f的近似KF点，记为ε－KF点.

定义3[5]对于以上定义的映射对(T,G)，如果∃εk＞0，k∈N，当k→∞，εk→0时，有函数f的εk－KF点列yk→y*，同时T(ε)逼近X，且y*∈X为函数f的一个KF点，那么称y*为函数f的稳定KF点，记为(T,G)－稳定KF点.

引理2[5]设X为Hausdorff线性拓扑空间E中的非空紧凸集，R为实数集，f：X×X→R，且(T,G)为一正则映射对，则函数f在X×X上存在(T,G)－稳定KF点.

2 主要结果

首先引入策略集的扰动映射χ：

设集值映射χi：[0,1]→Xi，i∈N，∀ε∈[0,1]，记χ＝(χ1,…,χn)，X＝X1×X2×…×Xn，又记int(X1×X2×…× Xn)为X1×X2×…×Xn的内部，且χi满足以下条件：

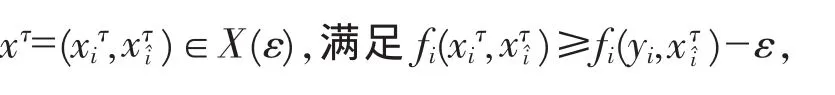
定义5设映射χ满足条件Ⅰ）和Ⅱ），如果∃εk＞0，k∈N，当k→∞，εk→0时，有对策P的εk－Nash平衡点列xk→x*，且x*∈X为(T,G)－稳定KF点[5]，则称x*为对策P的χ－稳定Nash平衡点.

定理1设映射χ满足条件Ⅰ），Ⅱ），对策P(N;X;f)满足：

1）对任意i∈N，Xi为Hausdorff线性拓扑空间中的紧凸集；

则对策P存在χ－稳定Nash平衡点.

证首先，证明对策P的ε－Nash平衡点是存在的.

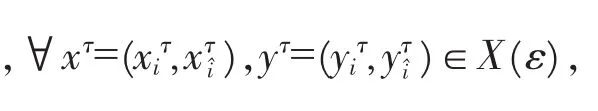
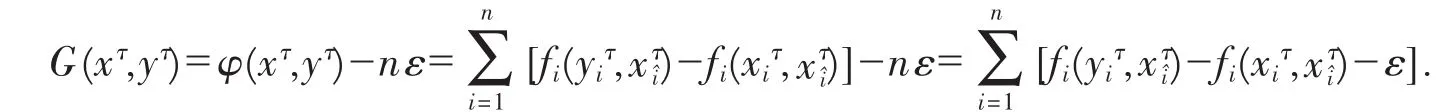
则容易验证∀xτ∈X(ε)，G(xτ,xτ)＝－nε＜0.

对每一yτ∈X(ε)，xτ→G(xτ,yτ)是下半连续的；

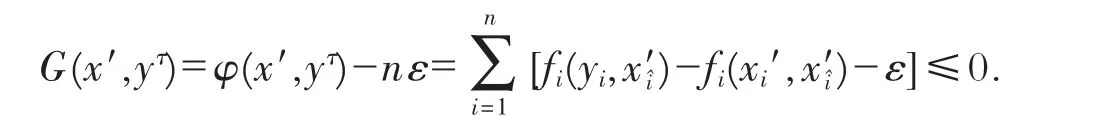
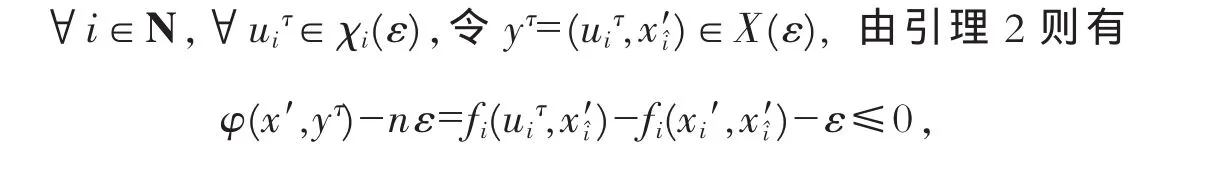
这时由φ(x′,yτ)≤nε，其中nε→0，并且函数φ满足文献[5]中的条件，则x′为ε－KF点.

∀εk＞0，当k→∞，nεk→0时，任取对策P的εk－Nash平衡点列｛xk｝⊂X，因为X为紧集，存在x*∈X，使得x*是｛xk｝的聚点.不妨设xk→x*∈X，这里，xk为函数φ的εk－KF点，由引理2可知，x*为函数φ的(T,G)－稳定KF点，从而为对策P的χ－稳定Nash平衡点.

[1]俞建.Nash平衡的存在性与稳定性[J].系统科学与数学,2002,22(3)：296-311.

[2]YU Jian.Essentiai equilibria of n-person noncooperativegames[J].Toumal of Mathematical Eeonmiesl,1999,31：361-372.

[3]俞建.博弈论与非线性分析[M].北京：科学出版社,2008：39-63,83-85.

[4]VANDERLAAN G,TALMAN D,YANG Zaifu.Refinements of stationary points with applications to noncooperative games and economics[J].SIAM Journal on Optimization,2006,16：854-870.

[5]冯冰,杨辉.定义域的扰动下Ky Fan点稳定性的研究[J].贵州大学学报：自然科学版,2008,25(3)：242-244.

The Refinements of Nash Equilibrium under the Perturbation of Strategy Sets

FENGBing
(School of Humanities&Social Sciences,Guangdong LingnanInstitute of Technology,Guangzhou,Guangdong 510663,China)

To define a perturbation mapping of strategy sets and give a new concept about the stable Nash equilibrium,the existence of itby anoutcome of the Ky Faninequality is studied.

ε-Nash equilibrium；χ-stable Nash equilibrium;perturbation；refinement

O225

A

1009－8445（2010）05－0008－03

（责任编辑：陈静）

2010－05－09

冯冰(1984－),女,广东徐闻人,广东岭南职业技术学院博雅教育学院助教,硕士.