基于改进遗传算法的多目标配电网重构

周 丹，辛 江，马志刚

（1.北京大兴电力公司,北京102600;2.石家庄供电公司，河北 石家庄050000）

0 引言

配电网络重构是一个多目标非线性混合优化问题[1-7]，已经发表的配网重构方法有以下几种：数学优化理论算法，如分支定界法，它存在严重的“维数灾”问题；启发式方法，如支路交换法[8]、最优流模式算法[9]，它们缺乏数学意义上的全局最优性；人工智能算法，如神经网络法[10]、模拟退火法、遗传算法（GA）[11-23]等，这些方法在保证得到全局最优解方面效果很好。人工智能算法中遗传算法只需要目标函数本身，而不需要目标函数的导数或其他辅助的信息，因而具有广泛的适应性[23]。但该算法同样还面临许多问题，如计算速度慢，距离在线应用的要求还有一定的距离；用遗传算法解决电网重构的主要问题是计算过程中生成过多不可行解，易产生早熟现象，计算效率低下，以及生成染色体解的范围过大，存在难以承受的计算代价。人们开始对如何减少算法时间和提高算法效率进行研究，文献[24]针对遗传算法的编码方式做了一定的改进，采用了直接编码方案，并提出通过模糊规则在线地改变交叉率和变异率的值，改进了算法性能，提高了收敛速度，避免了不成熟收敛。由于配电网重构的结果必定为辐射型网络，文献[25]提出了一种减少生成树数量的重构算法，但最终要一一计算，比较减少后的每棵树的网损。

针对遗传算法存在的问题，结合前人的改进方法，对遗传算法在综合考虑降低网损收益和开关操作费用的多目标重构问题进行全面分析，导出不影响最优解前提下的必选择支路，缩小了可行染色体解空间范围；改进了原有遗传算法的二进制编码方式和遗传操作，采用支路实数编码和与之对应的遗传操作，提高了遗传算法的计算效率；最后将编码方式与辐射状网络潮流计算[26-27]结合起来，使之能够给潮流计算提供关联矩阵等重要中间变量，加快适应度函数的计算。综合以上几个方面的改进，使遗传算法计算时间大大减少，并且理论上能够保证得到全局最优解。

1 配电网重构的数学模型

按照不同的场合和目的可以定义不同的重构模型，一般来说，其数学模型描述如下

式中，f(S,X)是数学模型的目标函数；S为控制变量；X为状态变量；h是等式约束；g为不等式约束；T为所求问题的解空间。

1.1 目标函数

1)考虑开关操作次数最少。

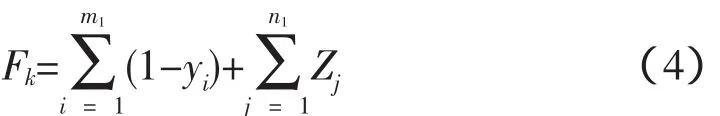
式中，yi和Zj分别是表示分段开关和联络开关在重构后的状态，闭合时为1，断开时为0；m1和n1分别为配电网中的分段开关和联络开关数。

2)考虑网损最小。

式中，ri是馈线上的阻抗；Pi和Qi分别是馈线i上流过的有功功率和无功功率；Ui为馈线i上的电压；FC为网络中所有闭合馈线的集合。

本文为使配电网在一段时间T内的收益最大，并且综合考虑降低网损的收益和开关的操作费用，得到配电网重构的多目标函数：

式中，k1为单位电价；T为重构时间间隔；Ploss1和Ploss分别为重构前后的网损；k2为开关操作一次的费用；Fk为重构一次的开关操作次数。

1.2 罚函数

对于节点电压，其罚函数为：

式中，m1和m2表示惩罚程度，为大于0的常数，通常取2。

1.3 综合目标函数

将g1和g2加入到原目标函数F中，得到新的目标函数f：

式中，β1和β2均为大于0的常数，称惩罚因子。

2 改进遗传算法

2.1 编码策略

由于电网中的开关数量巨大，采用0-1编码染色体的长度十分惊人，编码解码的计算量都会很大，不利于缩短计算时间。为了加快重构速度，采用十进制的非常规编码方式，选择断开的支路编号作为基因编号。将所有支路都闭合，这样网络中将形成一些环，依次打开这些环，系统就恢复到辐射状的结构。设环的个数是N，每个环路当中的支路形成一个集合，每个集合中选取一条支路断开，每个集合中选择出的支路编号成为染色体的一位，最终染色体长度为N。

以一典型的三馈线系统为例，见图1，共有16条支路，按照一般二进制编码方式染色体长度为16，则染色体空间将有216=32 768个个体。通过数学组合可以得出图1中可行染色体个体为60个，二进制编码有效候选解只占60/32 768=0.183 11%，搜索效率非常低。应用十进制编码，闭合所有支路，系统中有3个环集合存在，它们分别是（1、5、10、9、7、6）、（6、11、16、15、12）、（1、2、3、4、14、13、12），此时生成染色体空间中个体数目为=210,有效候选解占60/210=28.571%，搜索效率与二进制相比得到了很大提高。

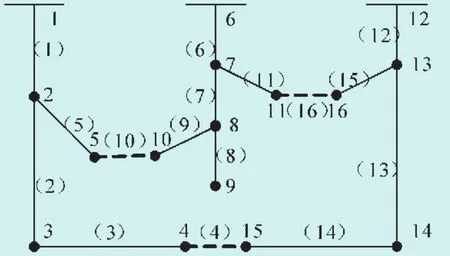
图1 IEEE典型三馈线系统

基于图论理，论文献[28]给出了以网损最小为目标函数时必须闭合支路的一般规则：与电源点相连的支路开关一般应闭合。文献[24]根据基于理想网络的规则，导出了不影响解最优性的必须闭合支路开关的规则。应用这2条规则，系统中支路1、6、12为必须闭合支路，将它们从个个环路空间中删除，进一步减小了解空间范围，此时染色体空间中个体数目为60。此系统由于馈线多而环路少造成了生成的染色体空间恰好等于可行解空间，但是应用上述规则确定出必闭合支路一定能够减少染色体空间的范围。

2.2 初代染色体生成

初始种群依次从N个环路集合中随机选取的方式生成，每生成染色体的一位都要判断系统连通性，过程如下：以图1系统为例，系统中存在3个环路集合，经规则约简后为I（5、10、9、7），II（11、16、15），III（2、3、4、14、13），随机从这3个环路集合中选取一个集合，从这个集合中随机选取一条支路作为染色体的第一个基因，设选中I集合中的10支路。从剩下的2个环路集合中选取一个，在集合中随机选取第二条支路，判断网络连通性，连通则选取的支路编号作为染色体的第二个基因，否则从该集合中重新选取开关，再验证连通性，直到找到一个适合的支路，设选中II中支路16，判断系统连通，16为染色体的第二个基因。依此类推，选中III中的4号支路，打开系统所有环路，形成一个合法的染色体（10、16、4）。

每形成一个合法染色体后还要检查该染色体是否和已经形成的染色体有重复，有则舍弃，重新生成。最后检查总的染色体数目是否达到种群规模，是则停止，否则继续生成下一个个体。

2.3 交叉和变异

由于应用十进制编码方式，大大减小了染色体长度，避免了对不必要基因的遗传操作。采用单点交叉的方式，交叉概率取0.5。随机选取交叉点，交换父、母染色体中该点基因，形成2个新的个体，每交换一个基因都需要验证交换的合法性（交换后网络是否连通）。如果2个后代都不合法，则重新选取父母进行交叉，直到产生至少一个合法个体。交叉产生的合法后代不进行比较，全部直接进入下一代。

十进制的编码方式，变异操作不同于二进制编码的变异位基因取反，所采取的办法是：随机选取一位变异基因，用该基因（支路）所属环中的另外一条支路来替换它。实验证明，如果随机选取替换支路，形成非法染色体的概率很大，这里从变异基因对应支路的相邻支路中选取，若左右相邻支路都不符合标准，则寻找第二个相邻支路，依此类推。

结合十进制编号配网重构的特点，变异操作对寻优的影响较大，应取较高的变异概率，但当变异概率过高时，可能会使当代最优解发生变异从而偏离最优，通过试验本文中变异概率取0.5。

2.4 连通性判定

网络拓扑辨识问题通常使用搜索算法（广度优先、深度优先），这些算法一般使用链表法描述网络结构，在求解过程中需要完全占用CPU时间[28]。本文采用基于关联矩阵法的网络拓扑辨识算法，辨识速度快，具有很强的实时性。具体操作如下：

根据华沙尔算法定义矩阵乘法运算：

此时公式（10）中A为网络节点-支路关联矩阵，用A表示，式（10）中B为节点-支路关联矩阵的转置AT，C=A·AT=[cij]表示了节点i与节点j通过任意支路的关联情况，若cij=1则必有支路连接ij节点，矩阵C称为一级节点—节点连通矩阵，计为C1。运用连通关系C2=C1·C1，求得C2它代表了节点之间的部分连接关系，依次类推，直至C阵不再变化为止。若C阵为一全1矩阵，则表示矩阵连通，否则非连通。

3 树状网潮流计算

3.1 前推回代

在系统网络损耗最小的单目标优化问题当中，文献[25]以网损的倒数作为适应度函数,方法简洁有效。本文也采用此种方法。适应度函数的计算时间很大程度上影响着整体算法的时间。通常的牛拉法、PQ分解法在辐射网潮流计算时，常常会出现收敛问题，计算速度较慢，前推回代法能够很好解决这个问题。此次应用支路电流计算染色体适应度。

式中，I觶Ni为节点i注入电流矢量；S觶i为节点i注入功率；V觶i为节点i电压。

式中，A为电源点添加无源虚拟支路的节点-支路关联矩阵（电流流入方向为负）；U是为与A同阶的单位阵；A0是对角元素为“0”，非对角元素与A完全相同的矩阵。

式中，I觶L为支路电流列矢量；I觶N为节点注入电流矢量。

显然，式（14）左端最后一个元素，即最后一个支路电流等于它末端节点注入电流的负值（I觶N取注入节点为正方向），因而采用回代的方法就可以很容易将各支路电流求得。

电压电流的关系式为：

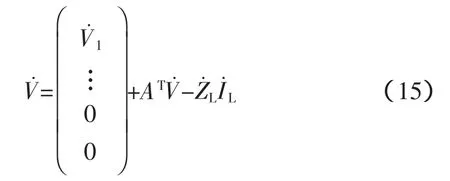
显然，式（15）左右两端第一个元素均为V觶1，应用前推方法，给定根节点电压，由第二行开始计算，即可将各节点电压求得。具体步骤为：

1)设定各节点电压初值V(0)，其中根节点电压为给定值V1；

2)由各节点电压值求得各节点注入电流；3)由式（14）计算各支路电流；

4)由给定根节点电压V1，以式（15）计算各节点电压；

5)检查是否满足收敛条件．若满足即结束计算，否则返回2)进行计算。

3.2 二次编号

前推回代法之所以能够快速计算系统潮流，很大程度上是由于特殊的编号方式（沿着供电的路径，节点编号依次增大），使得A阵为一上三角矩阵，回代变得很方便。而随机生成的染色体对应网络可能改变线路的功率方向，即原来编号大的节点功率流向编号小的节点，这样形成的A阵不是一个上三角矩阵，不能用于回代计算，需要进行二次编号。

具体做法如下：采用深度优先搜索方法搜索整个网络，记录各个节点搜索的先后顺序，按照搜索的先后顺序依次对节点进行重新标号，新编号的节点满足从节点0沿供电路径节点编号依次增大的要求。对应将支路编号，支路编号与它所连接的末节点新编号相同。将原节点、支路的信息赋给新的节点、支路，从而完成二次编号操作。

二次编号是计算适应度时候的内部编号，为了使前推回代得以进行，二次编码操作只适应在计算染色体适应度函数中，在遗传算法的其他操作中仍沿用以前的编码方式。

4 算例结果及分析

本算例采用如图2所示的美国PG&E的69节点配电系统。额定电压为12.66 kV，总负荷为3 802 kW+j2 694 kV·A。其他参数定为：基准功率100MV·A，基准电压12.66 kV。对该配电网进行简化处理，线路1-2，2-3，3-28，28-29，29-30，30-31，31-32，32-33，33-34，34-35，8-40，40-41，12-57，57-58，11-55和55-56之间的开关均不能断开，否则就会有孤岛出现。

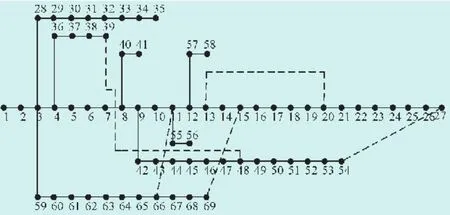
图2 美国PG&E的69节点配电系统图

用本文算法与文献[29]模糊自适应遗传算法的对比计算结果如表1所示。

由表1可知，本文的重构方法需打开隔离开关14-15，47-48，50-51，闭合联络开关15-69，27-54，39-48，开关操作6次，比文献[29]的开关操作费用多，但是利用本文的方法有效降低了网损，提高了电压质量，并且在重构时间间隔T为24 h时，总收益比文献[29]高，进一步验证了本算法的可行性。

表1 配电网重构前后各项指标比较

按本文的方法，连续运行优化程序50次，最好的一次迭代到17代就收敛，最差的一次是迭代到42代收敛，大部分在30代左右收敛。

5 结论

本文综合考虑降低网损的收益和开关操作的费用，使配电网在一段时间T内的收益最大，得到配电网重构的多目标函数。以美国PG&E的69节点配电系统为算例进行了试算，并对仿真结果进行了具体分析，验证了用于配网重构实数编码的遗传算法的有效性和快速收敛性。实例表明所用方法对于避免陷入局部最优解或接近全局最优解显示了良好的优越性，进一步拓展了遗传算法在配电网络重构中的应用。

[1] 王磊，吕娟，张强.基于最小生成树算法的配电网络重构[J].陕西电力，2009,37（1）:13-17.

[2] 张红云，钟筱军，毕鹏翔，等.配电网开关优化方法研究及应用[J].陕西电力，2008,36（11）:21-24.

[3] 赵俊光，唐恒海，江洁.确定配电网最佳无功补偿点位置及容量的优化方法[J].陕西电力，2009,37（8）:1-4.

[4] 刘晋，苏虎成，袁喆，等.基于序贯仿真法的复杂配电系统可靠性评估[J].陕西电力，2009,37（6）:17-20.

[5] 王李娟.基于IEC61850的配电网络馈线自动化终端[J].陕西电力，2009,37（6）:59-62.

[6] 黄庆，董家读，黄彦全.一种新的配电网无功优化算法[J].陕西电力，2009,37（2）:22-25.

[7] Roytelman I,Melnik V,Lee SSH,et al.Multi-Objective Feeder Reconfiguration by Distribution Management System[J]．IEEE Trans on PWRS,1996,11（2）：661-667．

[8] Debapriya Das.A Fuzzy Multiobjective Approach for Network Reconfiguration of Distribution Systems[J].IEEE Transon Power Delivery,2006,21（1）:202-209.

[9] 邓佑满，张伯明，相年德.配电网络重构的改进最优流模式算法[J].电网技术，1995，19（7）：47-50.

[10]Kim H,Ko Y,Jung K H.Artifieial Neuarl-Netwok Based Feeder Reconfiguration for Loss Reduction in Disrtibution Systems[J].IEEE Transaction on Power Delivery,1993,8（3）:1356-1366.

[11]马玲，袁龙，张泽.基亏遗传算法的电网优化规划[J].陕西电力，2008,36（11）:56-60.

[12]张蕾，王高平.一种改进的共同进化遗传算法及其应用[J].现代电子技术，2008,31（14）：132-134.

[13]冯建宇.配电网络重构的环路分解遗传算法[J].陕西电力，2008,36（6）:39-43.

[14]陈燕，徐建军.基于遗传算法的MPLS-VPN数据网络规划模型的研究与实现[J].陕西电力，2008,36（2）:19-23.

[15]潘舒，吴陈.基于遗传算法的关联规则挖掘[J].现代电子技术，2008，31（2）：90-92.

[16]王喜刚，翟智勇，杨海波.基于遗传算法的无功电压控制分区研究[J].陕西电力，2009,37（7）:37-40.

[17]苏煜，王薇.一种适用于配电网络重构的改进遗传算法[J].陕西电力，2006,34（8）:26-29.

[18]赵俊光，梁科，李洪旭.电力系统无功优化改进遗传算法的研究[J].陕西电力，2009,37（2）:1-5.

[19]宋鹏，徐彤.基于遗传算法斜向探测电离层参数反演研究[J].现代电子技术，2008，31（19）：16-18.

[20]王磊，庄园.基于最小生成树算法和改进遗传算法的配电网络综合优化[J].陕西电力，2009,37（12）:9-13.

[21]周巧俏，汤云岩，海晓涛.基于改进自适应遗传算法的分布式电源的选址和定容[J].陕西电力，2010,38（2）:40-44.

[22]NaraK,ShioseA,KitagawaM.ImplementofGeneticAlgorithm For Distribution Systems Loss Minimum Reconfiguration[J].IEEE Trans.on Power system,1992,7（3）:1044-1051.

[23]余贻鑫，段刚．基于最短路算法和遗传算法的配电网络重构[J]．中国电机工程学报，2000，20（9）:44-49.

[24]刘莉，陈学允．基于模糊遗传算法的配电网络重构[J].中国电机工程学报，2000,20（2）:66-69.

[25]王威，韩学山，王勇，等.一种减少生成树数量的配电网最优重构算法[J].中国电机工程学报，2008，28（16）:34-38.

[26]张学松，柳焯，于尔铿，等．配电网潮流算法比较研究[J]．电网技术，1998，22（4）:45-49.

[27]张尧，王琴，宋文南，等．树状网的潮流算法[J]．中国电机工程学报，1998，18（3）:217-220.

[28]毕鹏翔，刘健，刘春新，等．配电网重构的改进遗传算法[J]．电力系统自动化，2002，1（25）:57-61.

[29]张忠城，王淳.模糊自适应遗传算法在配电网络重构中的应用[J].江西电力，2006，30（2）:6-8.