变压器健康状况评估与剩余寿命预测

2010-09-03梁博渊杨欣桐

电网与清洁能源 2010年11期

梁博渊，刘伟，杨欣桐

（1.华北电力大学电气与电子工程学院，河北保定 071003；2.河北省电力研究院，石家庄 050021）

0 引言

随着电压等级的提高和电网规模的扩大，对电网内运行设备，尤其是核心设备电力变压器的可靠、健康运行提出了更高的要求。通过对变压器进行剩余寿命分析、状态评估并采取相应的寿命延长技术，可以有效地提高变压器的可靠性与经济效益。

目前，国内外专家学者通过神经网络、模糊理论、贝叶斯网络、专家系统、粗糙集理论等方法，结合对变压器预防试验数据、运行工况等建立相应的变压器故障诊断或状态评估模型[1-6]，研究广泛，理论较为成熟。由于变压器结构本身的复杂性，以及导致变压器突发故障原因的不确定性，对变压器剩余寿命进行准确的分析预测十分困难，该领域目前的研究主要是通过分析变压器糠醛含量来对变压器的固体绝缘性能进行评估，再根据绝缘状况来确定变压器的可靠性及剩余寿命。

本文建立了电力变压器状态评估的三级模型，在评估模型中引入英国EA公司的电力设备健康状况老化公式，根据老化公式，推导出基于健康状态值的剩余寿命及故障率判断公式，并应用该模型对一座500 kV变电站变压器进行健康状态评估、剩余寿命预测、未来健康状况预测。

1 变压器状态评估信息的确定

电力变压器的老化通常是指绝缘的老化。变压器投运后，电场和磁场共同作用，温度升高，负荷增加，加快了变压器的老化进程；运行期间，偶然发生的过电压、短路故障，导致变压器绕组瞬间大电流，温度急剧升高，严重损坏了绝缘的耐压强度[7]。图1形象模拟了变压器健康状况的老化进程。

对变压器老化进程进行研究分析后，进而确定变压器的各个状态信息量，把状态信息分为基础信息、运行信息、试验信息、故障缺陷信息4部分。

1)基础信息：基础信息为变压器自身所固有的信息，包括变压器的额定容量、额定电压、额定电压比、绝缘水平、空载损耗和空载电流、负载损耗和短路阻抗、绕组联结组标号，同时还有冷却方式、变压器油温升、绕组温升，还包括制造厂家、出厂日期、投运日期，及本系列设备的家族缺陷等。

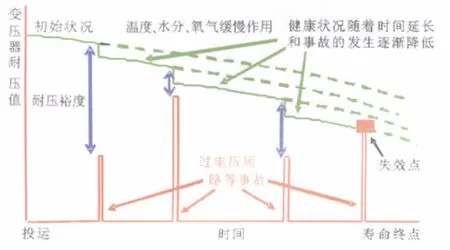
图1 电力变压器老化进程模拟图

2)运行信息：运行信息为变压器运行期间状态信息的记录，包括变压器的负载情况、变压器外部所在环境情况（温度、污秽等级）、冷却系统的工作状况和调压开关的工作状况等其他辅助机构的状态信息。

3)试验信息：包括油化试验（酸度、击穿电压、微水、介质损耗）信息、油色谱试验（氢气、甲烷、乙烷、乙烯、乙炔）信息、糠醛试验信息。

4)故障缺陷：变压器最近5 a的各种故障信息（包括故障大小、故障持续时间、维修更换情况等），如短路故障（要有故障电流、故障时间记录，故障后的直阻测试、电容量测试、频谱测试分析等）。

2 变压器状态评估模型的建立

2.1 一级评估模型

本文将变压器状态评估模型分为三级。第一级评估模型选用对变压器状态最重要的指标，这些指标直接反映变压器主体的健康状况、投运的时间长短及此期间健康值损失，包括生产厂家、型号规格和设计寿命、投运年限、运行负荷、运行环境指标。具体的评估模型如图2所示。

图2 电力变压器健康状态评估一级模型

一级评估模型的评估结果为一个值在0~10的健康指数，其值与变压器的设计寿命、运行负荷、投运年限、运行环境成一定的比例或指数关系。

2.2 二级评估模型

二级评估模型主要针对油色谱试验数据、油质试验数据、糠醛含量数据进行评估。这些试验数据是对变压器健康状况的间接反映，把这些数据与标准数据和前期数据进行比较，就可以反映出当前变压器的健康变化情况，其评估模型的结构图如图3所示。

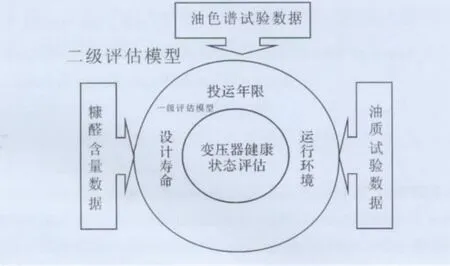
图3 电力变压器健康状态评估二级模型

2.3 三级评估模型

三级评估模型如图4所示。三级评估主要用三个系数F1、F2、F3对一、二级模型评估出的健康指数进行修正。F1是外观状况修正系数，是由变压器主体反映的实际状况得到的；F2是故障及维修系数，是由变压器前期的故障、缺陷情况，结合工区的维修、更换配件等情况得到的；F3是附件系数，是由变压器几个重要附件的实际健康状况决定的。评估最终得出健康指数HI、剩余寿命EOL。

图4 电力变压器健康状态评估三级模型

3 评估模型中系数与权重的确定

3.1 健康水平指数计算公式

在本文所建立的评估模型中，引入了英国EA公司的一个健康指数计算公式，该公式是基于设备老化原理、体现设备健康水平指数随时间变化过程的一个经验公式，目前广泛应用于英国和北美电力设备的健康状态评估。健康水平指数计算公式为：

式中，HI0为设备的初始健康水平指数；HI为设备最终的健康水平指数；B为老化系数；T1为与全新设备HI0对应的年份，一般为设备投运年份；T2为与所要计算的对应的年份，可为当前年份，也可为未来年份。

健康水平指数的取值范围为0～10，其值越低表示的设备状态越好。健康水平指数处于0～3表明设备状态良好；健康水平指数处在3.0～6.5表明设备已经出现比较明显的老化现象，且老化过程开始明显上升；健康水平指数＞6.5时，表明设备已经出现严重的老化现象，在此状态下，故障发生概率明显上升。

3.2 评估模型中各指标权重的确定

本文所建立的变压器状态评估模型是分层次的多指标综合评判，需要赋予各指标合理的权重，以正确反映它们在同一层次评估中不同的重要性。本文通过多位专家群组决策，采用层次分析法[8-9]对各指标赋予权重，计算结果见表1、2。

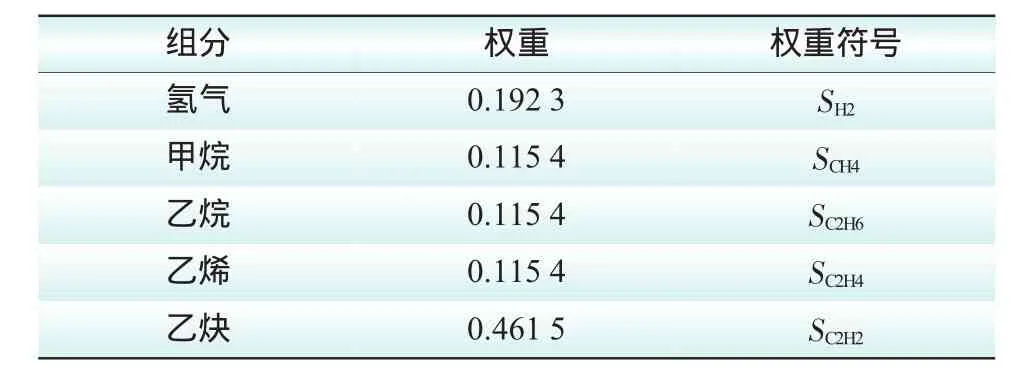
表1 变压器油色谱试验主要气体权重表

表2 变压器油质试验各因素权重表

3.3 一级评估模型中各系数的确定

1）老化系数B的确定。由式（1）可得：

设T′exp=T2-T1，为基于变压器设计运行年限的预期运行年限。假设当变压器运行T′exp年后，其健康状态明显劣化，处于寿命的终结，此时其健康指数HI将达到6.5，事故率非常高，马上就要坏掉。变压器初始健康水平指数HI0为变压器投运时的健康指数，一般取0.5。由此，式（2）满足如下关系：

2）设备预期寿命T′exp的确定。电力变压器在进行产品设计时，就已经基本确定了其使用寿命。但不同的生产厂家、不同的生产技术及工艺都可能对所生产的设备的质量和寿命造成一定的影响；此外，即使是在同一时间、同一工厂生产的不同批次的产品都可能存在质量上的差异，因此，在考虑设备的设计寿命时，本文先通过用户对设备质量的掌握情况，根据设备的厂家和型号规格设定一个预期的使用寿命Texp，再利用负荷系数和环境系数对其进行修正：

在设备正常运行、没有外来因素（如出口短路等）影响的情况下，电力变压器的负荷对其健康状况的影响起决定作用。一般来说电力企业对变压器的负荷情况管理比较严格，变压器负荷率用百分比表示，通常控制在40%~60%最佳。变压器负荷系数取值见表3。

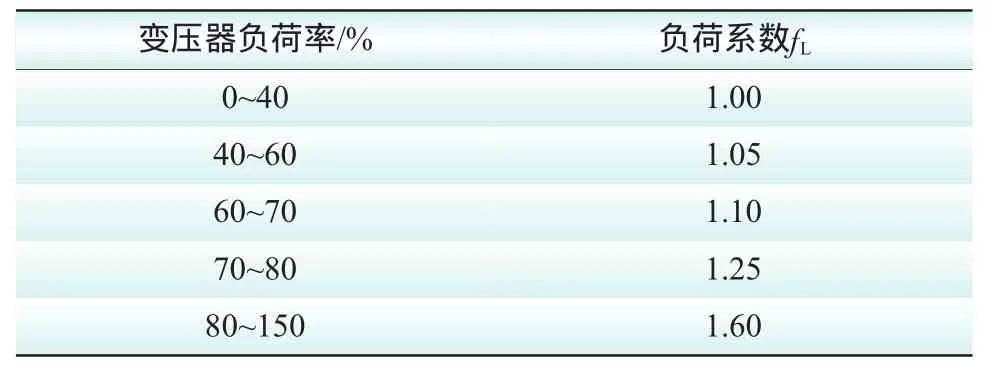
表3 变压器负荷系数表

变压器负荷率是指变压器运行中所承载的平均负荷与变压器额定容量之比：

3）环境系数的确定。不同地区、不同环境污染程度、年平均气温、湿度、当地的污秽等级对变压器的安全运行、使用寿命都有较大影响。对环境温度的要求是：最高气温40℃，最高日平均气温30℃，最高年平均气温20℃，最低气温-25℃。高相对湿度易繁殖霉菌，影响金属的耐腐蚀性能。污秽较严重的地区，比如附近有水泥厂，空气中灰尘含量对外部绝缘套管有很大影响，环境系数取值见表4。

在得出老化常数B之后，根据变压器健康指数公式得出老化健康指数HI1：

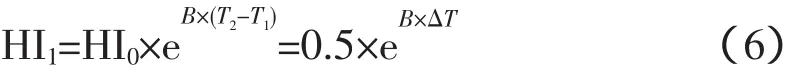
式中，ΔT为设备的投运年限。

表4 变压器环境系数表

3.4 二级评估模型中各系数、权重确定

1）HI2a确定[10-11]。HI2a由油色谱试验数据确定，计算步骤如下：

根据H2，CH4，C2H6，C2H2，C2H45种气体的测试结果，分别计算气体的含量等级V，具体分级规则如表5所示。

表5 变压器油色谱试验主要气体含量分级表

将各项目试验等级V乘以对应项目权重，计算各种气体组分分值：

2）HI2b确定[12-13]。HI2b主要由油质试验决定，计算步骤如下。

根据酸度、击穿电压、微水、介质损耗的测试结果，分别计算各测试项目的试验等级U，具体分级规则如表6所示。将各项目试验等级U乘以对应项目权重，计算各种气体组分分值：

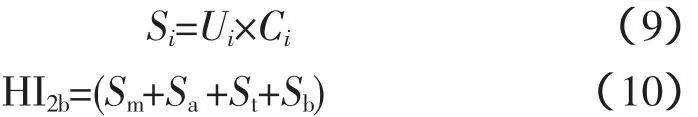
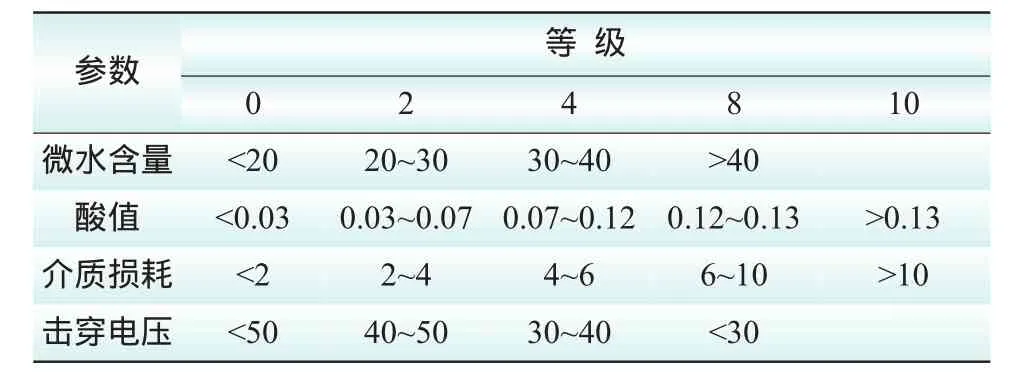
表6 变压器油质试验各因素分级表

3）HI2c确定[14]。HI2c由糠醛试验数据确定。糠醛是绝缘材料碳-碳分子链断裂的产物，它直接反映绝缘的老化状况，碳碳链的断裂程度用聚合度表示。一般新的绝缘材料聚合度为1 000，聚合度低于250时需引起注意。纸的聚合度和糠醛含量（FFA）之间满足经验公式：

当FFA＝5时，DP＝250，这时反映出变压器的绝缘已经达到其使用寿命HI=7；当FFA＝0.01时，DP=1 000，绝缘为全新状态HI=0.1；可得出计算公式：

4）综合健康指数HIcom。综合健康指数HIcom是根据HI1、HI2a、HI2b、HI2c的组合计算的，具体逻辑关系如下：

当HI1为最大时：

当HI1为非最大时：

式中，fcom是一个系数，在不同情况下，根据对应规则取值也不同。

3.5 三级评估模型中各系数的确定

1）外观修正系数。由变压器主箱体、冷却系统、管道系统、调压开关、其他辅助机构4个部分的外观状况查表得出对应系数决定，取值为4个部分中的最大值，变压器外观修正系数如表7所示。

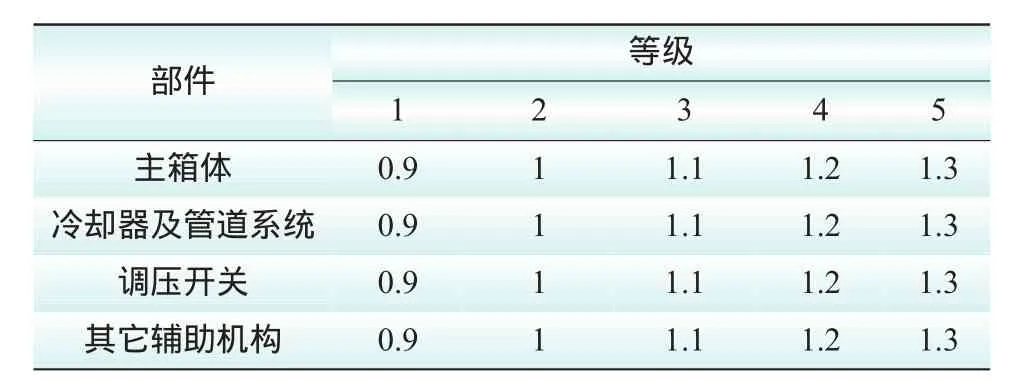
表7 变压器外观修正系数表

2）缺陷修正系数。F2是根据变压器过去5 a中发生的各类故障缺陷等级次数乘以对应的缺陷等级，累加得到变压器的缺陷等级：

缺陷等级＝一般缺陷次数×一般缺陷基数＋严重缺陷次数×严重缺陷基数＋紧急缺陷次数×紧急缺陷基数。缺陷系数取值如表8、9所示。

表8 变压器缺陷基数表

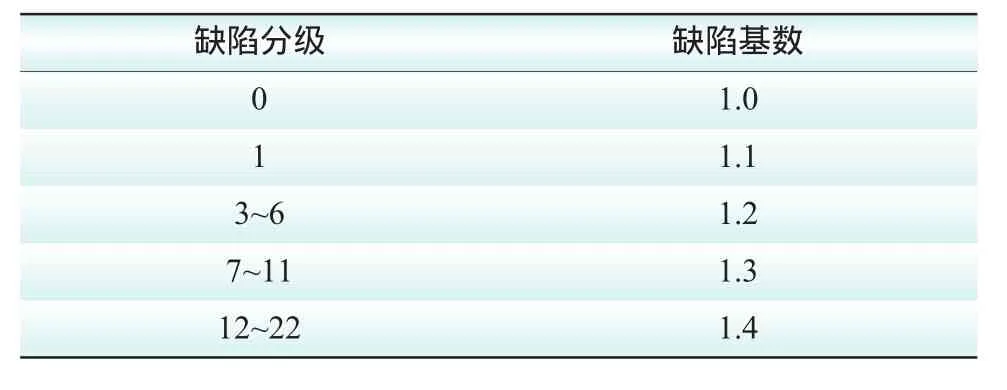
表9 变压器不同缺陷等级系数表

3）套管可靠性系数F3。F3是根据变压器套管型号，考虑现场应用中各型号的可靠性，对其进行分级，如表10所示。

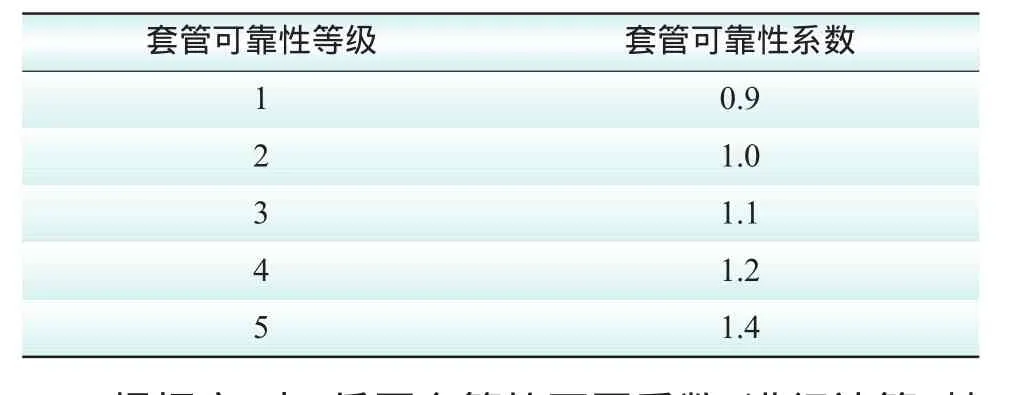
表10 变压器套管可靠性系数表

根据高、中、低压套管的不同系数，进行计算，基本逻辑关系如下：

① 若max（高、中、低）>1，则F3＝高、中、低系数之积；② 若max（高、中、低）≤1，则F3＝min（高、中、低）。

3.6 最终健康指数确定

1）最终健康指数HI。

2）剩余使用寿命。变压器的剩余使用寿命EOL是以变压器当前健康指数来推算到其报废的健康指数的时间。当健康指数到达7时，设备故障发生概率急剧上升，设备在此阶段需要采取相应的措施（如更换、大修等）。

由HI=HI0×eB×EOL，代入变压器寿命终点的健康值HI=7，可得7=HI0×eB×EOL，两边取对数，得剩余使用寿命公式：

3）未来健康指数HIn。根据健康指数的计算公式，及我们所要计算的未来年份，可以得出设备未来的健康指数HIn，其中n为未来年份，即ΔT

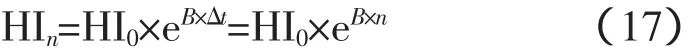
4 评估实例

4.1 状态信息

某变电站2号变压器A相电压等级为500 kV，生产厂家是保定变压器厂，型号规格为ODFPS-250000/500，出厂编号20073s04，出厂日期2007年4月1日，投运日期2007年4月25日，容量250MV·A，产品代号1BB.773.0311，产品型式DSOWODAF,空载损耗74.8 kW，空载电流0.078%，油种DB-25，体重201 t，油重57.8 t，接线组别Y0/Δ-11，接地方式为直接接地，调压方式为无载调压，运行环境为2级，变电站空气污秽等级为4级，冷却器有3组，高压套管型号为LB-500,中压套管型号为LRB-220，低压套管型号为LRB-35。该变电站额定负荷容量为1 500MV·A，过去5 a中最高负荷为501.1MV·A，预计未来5 a负荷与额定负荷百分比为0.634，相关试验数据如表11~14所示。

表11 42℃主箱体含气量、油色谱试验数据表 μL/L

表12 主箱体油简化试验数据表

表13 套管含气量、油色谱试验数据表 μL/L

表14 套管油简化试验数据表

4.2 评估过程

1）主健康指数HI1的计算。该变压器设计寿命是40 a，已运行1 a，处于环境污秽等级中等的地区，污秽等级为2，预计未来5 a负荷率在80%以上，该变压器所处的外部环境系数，查表3得fL=1.1；该变压器的负载系数，根据目前负荷及未来负荷预测，查表4得fE=1.05。

在计算出环境系数和负荷系数后，可以根据变压器预期寿命计算公式（4）计算，代入设计寿命、负荷系数、环境系数，可得2号变压器C相预期寿命：

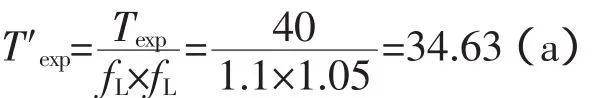
变压器老化系数是根据公式（3）代入数据计算得到的：

在得出变压器预期寿命T′exp和老化系数B后，根据变压器健康指数计算公式（6），代入数据，可得当前变压器主健康指数：

2）变压器健康指数HI2a、HI2b、HI2c的计算。HI2a为变压器油色谱试验数据确定的健康指数，由表5及表11试验测试数据，按照计算公式（7），由各气体组分的权重系数表1，可得：

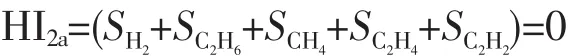
HI2b为变压器油质试验数据确定的健康指数，由表6及试验测试数据，按照公式（9），由表2试验项目的权重，按公式（10）求出HI2b：

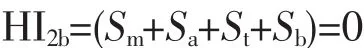
HI2c为由变压器糠醛含量测试数据确定的健康指数，根据公式及试验数据，可得：

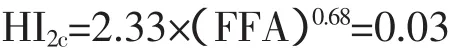
3）综合健康指数HIcom。综合健康指数HIcom是根据前面4个HI（HI1、HI2a、HI2b、HI2c）的组合计算，计算可得：

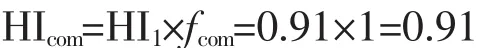
4）最终健康指数HI。变压器最终健康指数，是在计算出综合健康指数的情况下，根据变压器外观状况、曾经缺陷情况、附件（套管）状况，进行修正后，得到的一个客观值：

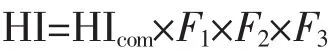
式中，F1为外观修正系数，根据现场评估结果结合表7，选最大修正系数得F1=0.9；F2为缺陷修正系数，投运以来没有发生过故障，查表8、表9得F2=1；F3为套管可靠性系数，根据现场情况及各项试验数据评估为高、中、低压套管，查表9并由其逻辑关系得F3=1。将数据代入公式可得最终健康指数：

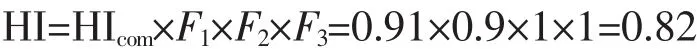
5）设备剩余寿命EOL。变压器的剩余使用寿命EOL是以变压器当前健康指数来推算到其报废的健康指数的时间。将计算所得老化系数B=0.1169代入剩余使用寿命公式，得出变压器的剩余使用寿命EOL：

6）未来健康指数HIn。根据健康指数的计算公式，及所要计算的未来年份，可以得出设备未来的健康指数HIn，其中n为未来年份，即ΔT。10 a后变压器预测健康指数为：

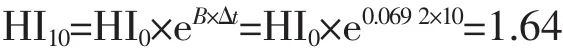
评估结果显示设备健康指数较低，表明设备目前故障率比较低，且10 a后设备健康指数仍比较低，说明设备的老化常数较小，设备所处的电网环境、外部环境都比较良好，这与目前设备的实际状况是非常相符的。

5 结论

本文建立了变压器状态三级评估模型，一级模型选用的状态信息量是对变压器状态影响最大的指标；二级模型选用的试验信息状态量是对变压器健康状况的间接反映；三级评估模型，选用由变压器主体反映出来的实际状况信息对前两级评估的结果进行修正。三级模型从整体对变压器的健康状态进行分析评估，使各项状态信息得到有效、充分利用。在评估模型中引入英国EA公司的电力设备健康状况老化公式，根据老化公式，推导出基于健康状态值的剩余寿命及未来健康指数公式。从电力变压器状态评估需要出发，运用层次分析法确定各级评估模型中各评判因素的权重，并应用该评估模型对一座500 kV变电站变压器的健康水平指数、剩余寿命、未来健康状况进行分析和计算，为状态检修的实施提供理论参考。

[1]安宗贵，李治平，王森.变压器油色谱远程在线监测与诊断系统[J].陕西电力，2010,38(6):50-54.

[2]王鹏，姜晓飞.基于模糊神经网络的变压器故障诊断技术与方法的研究[J].陕西电力，2010,38(5):53-56.

[3]王凯，王亚妮，张锋，等.变压器油纸绝缘老化状态的分析方法[J].陕西电力，2010,38(2):54-57.

[4]李军浩，郭磊，吕亮，等.变压器油老化对其局部放电及介质响应特性的影响[J].陕西电力，2009,37(11):1-4.

[5]姜晓飞，王鹏.基于油中溶解气体分析的变压器故障在线监测技术[J].陕西电力，2008,36(12):73-76.

[6]徐康健.变压器油色谱分析的灵敏性与油产地之间的关系[J].陕西电力，2008,36(7):60-62.

[7]尚勇，董明，赵文彬，等.油浸电力变压器固体绝缘老化的诊断[J].变压器，2002，39（12）：35-38.

[8]许树柏.层次分析法原理[M].天津：天津大学出版社，1988.

[9]Saaty T L.A Scaling Method for Priorities in Hierarchical Structures[J].JournalofMath Psychology，1997(15)：234-281.

[10]操敦奎.变压器油中气体分析诊断与故障检查[M].北京：中国电力出版社，2005:29-38.

[11]DL/T 722-2000 变压器油中溶解气体分析和判断导则[S].北京：中国电力出版社，2000.

[12]李军，董立文.油浸式变压器的老化和寿命评估[J].高电压技术，2007，33（3）:186-189.