Thomas-Fermi方程的特征分析与数值求解

杨秀德，吴 波，2

（1.遵义师范学院物理系，贵州遵义563002；2.西南大学物理科学与技术学院，重庆410075）

Thomas-Fermi方程的特征分析与数值求解

杨秀德1，吴 波1，2

（1.遵义师范学院物理系，贵州遵义563002；2.西南大学物理科学与技术学院，重庆410075）

Thomas-Fermi方程在处理核——电近似模型中占有非常重要的地位，但就方程而言，方程是非线性的，精确求解非常困难。作者通过一个简单的实例导出方程，分析了方程的具体特征,提出了一种方程有效的数值求解方法。

Thomas-Fermi方程；非线性微分方程；阿贝尔方程

在过去的几十年中，随着量子力学的建立，将量子力学应用到各领域成为关键问题，尤其在微观世界的认识方面更是热点。在处理微观原子世界的过程中，核——电构成的原子模型是大家关注的问题，除了少数简单体系可以精确求解以外，更多需要提出近似模型来处理多电子体系的微观世界。这其中一个成功的例子就是Thomas-Fermi—Dirac模型，虽然这个模型还很粗糙[1],但是在处理原子内部相关作用等问题上仍有许多值得利用的地方[2]。另外对此模型的讨论涉及到一个非线性微分方程——Thomas—Fermi方程，精确求解这个方程是非常困难的，因此许多人利用不同的方式进行近似求解[3，4]。本文从一个简单模型出发导出这个方程，分析了方程的特征和利用MATLAB系统进行数值求解，供大家参考。

1 模型的建立

在二体散射理论中，发生“碰撞”的两个粒子之间存在着相互作用势，如图1所示。若设这样的相互作用势为，引入折合质量μ=m1m2/（m1+m2）、相对位矢为相对速度为，根据牛顿运动定律，可以写出约化单体运动方程：

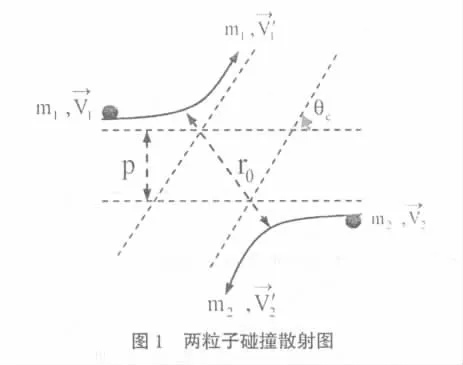
建立极坐标，根据能量守恒和角动量守恒定律，分析得出：

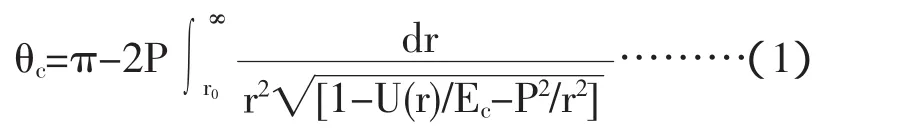
其中，Ec为质点系质心动能，P称碰撞参数。若采用库仑势（这里讨论斥力情况）来描述它们之间的相互作用，根据（1）式则有：

其中Z1、Z2、Ec均为已知。由于P是随机变化的，（2）式难于求解，但可以用近似理论去分析。若核外电子视为有一定密度的电子气，考虑核外电子云对裸库仑势的屏蔽作用，用一种建立在量子统计方法之上的Thomas-Fermi（TF）方法进行描述，最终可以得到Thomas-Fermi方程

其中x=r/aTF，aTF为屏蔽长度，Φ(x)满足Φ(x)，且满足以下定解条件：

2 方程的特征分析

由于方程是非线性的，求解较为复杂，一般都使用近似求解。而且在方程求解过程中，首先要分析方程的具体特征，从而选择合适的求解方法。

2.1 解的存在性和唯一性

Thomas-fermi方程解的存在性和唯一性可以通过卡拉西奥多里定理和马莫布里安尼定理[5]给出，可以证明方程（3）存在唯一的满足上述（4）式的三个定解条件的解。具体证明不在此赘述。

2.2 尺度变换不变性

对Thomas-fermi方程，可以作变量代换，令ξ= λx,z=λαΦ(x)：，若选择合适的α值为-3，则有：

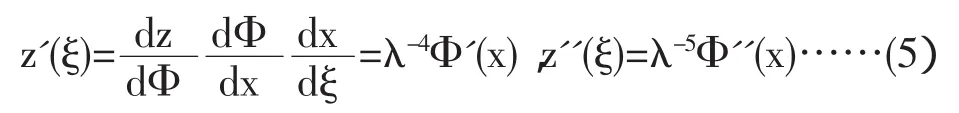
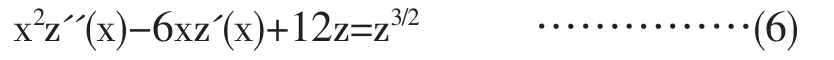
很明显，（6）式若作代换：ξ=λx，结果使得方程保持形式不变，说明方程为一种等尺度方程[6]。可以作变量代换：x=et，将（6）式变换为：

上式为常系数二阶微分方程，由于非线性项z3/2的存在，求这个方程的解析解也是相当困难的。

2.3 与阿贝耳方程的关系

对于（8）式，作分式变换：

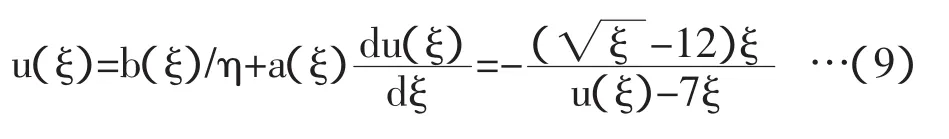
3 方程的计算机数值求解

这里，考虑到该方程与阿贝尔方程的变换关系，因此可以先求解阿贝尔方程，通过变量代换来达到最终求解Thomas-fermi方程的目的。但是考虑到方程的复杂性，可以采用数值求解。下面是利用Matalab进行数值求解的步骤和相应程序：

（1）差分法求解方程（10）；

（2）将求解的u（ξ）代回（9）式，便可以求得（8）式的解；

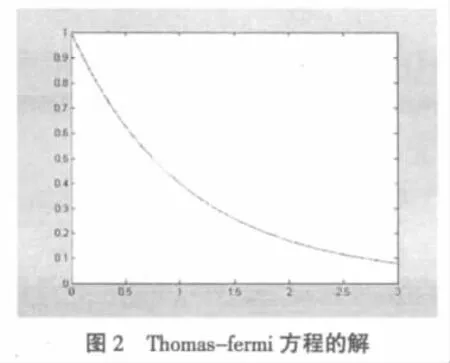
（3）再将（8）的解通过条件Φ=x-3ξ,x=exp（∫η(ξ) dξ）变换，将最终得到Thomas-Fermi方程（3）式的解。画出解的图形，如图2所示，即为本文得到的Thomas-Fermi方程的解。

以下为上述几步求解的Matlab程序：

%设置变量，定义初值

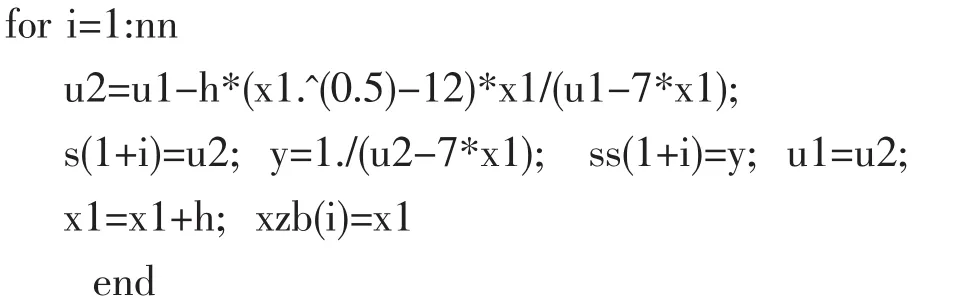
%差分法求解阿贝尔方程

%数值积分，代换变量

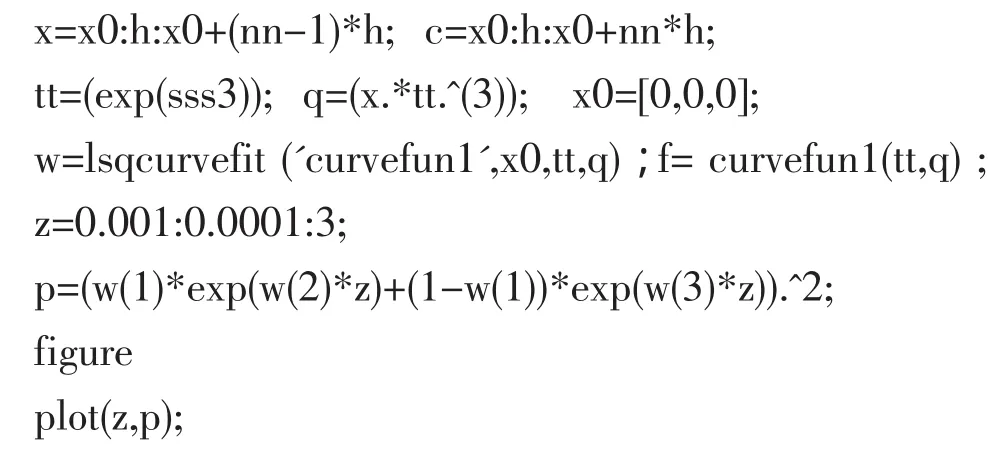
4 结论

Thomas-Fermi方程是一种非线性微分方程，在处理原子内部相关作用势方面有很多应用。本文从一个具体实例导出方程，给出了方程解的存在性和唯一性、等尺度特征以及与阿贝尔方程的关系等特征，最后利用MATLAB计算机数值求解，得到方程的近似解。当然，非线性方程的数值求解方式很多，本文方法仅供大家参考。

[1]R.N.Kesarwani.Improved variational solution of the Thomas-Fermi equation foe atoms[J].Physics Review A，1981，23(3)：991-998.

[2]Francisco M.Fernandez and J.F.Ogilvie.Approximate solutions to the Thomas-Fermi equation[J].Physics Review A，1990，42 (1)：149-154.

[3]高雁鸣.引力Thomas-Fermi方程的数值解[J].新疆工学院学报,1999,20(2)：96-99.

[4]V.Bush and S.H.Caldwell.Thomas-Fermi equation solution by the differential analyzer[J].Physics Review，1931，38：1898-1902.

[5]E.卡姆克.常微分方程手册[M].北京：科学出版社，1986.45-46，321.

[6]刘式适，刘式达.物理学中的非线性方程[M].北京：北京大学出版社，2000.21-22.

[7]E.卡姆克.常微分方程手册 [M].北京：科学出版社，1986.688-689.

[8]周大勇.基于Mathematica的特殊阿贝尔的可积性及其判定[J].大连铁道学院学报.2005，26(2)：6-9.

（责任编辑：朱 彬）

Characteristic Analysis and Solutions to the Thomas-Fermi Equation

YANG Xiu-De1,WU Bo1,2
(1.Department of Physics,Zunyi Normal College,Zunyi 563002,China;2.School of Physical Science and Technology, Southwest University,Chongqing 410075,China)

The Thomas-Fermi equation holds sway over nucleus-electron approximate models.But as to the equation,it is a nonlinear differential equation,so it is of difficulty to procure the exact solution.In this text we infer an equation from a simple example,analyze characteristics of equation,and put forward a valid numerical method at last.

Thomas-Fermi equation;Nonlinear differential equation;Abel equation

O232

A

1009-3583（2010）-03-0073-02

2010-03-12

遵义师范学院资金资助项目（基07013）；贵州省教育厅资金资助项目（2007B003）

杨秀德，男，贵州铜仁人，遵义师范学院物理系讲师，硕士，主要研究方向：计算物理和计算机辅助教学。