基于Levenberg-Marquardt算法的油田产量预测模型
2010-08-31翟亮亮王连堂王俊杰
翟亮亮,王连堂,王俊杰
(1.西安石油大学理学院,陕西西安710065;2.西北大学数学系;3.思茅师范高等专科学校)
基于Levenberg-Marquardt算法的油田产量预测模型
翟亮亮1,王连堂2,王俊杰3
(1.西安石油大学理学院,陕西西安710065;2.西北大学数学系;3.思茅师范高等专科学校)
针对标准的BP神经网络存在的缺陷,采用基于Levenberg-Marquardt算法改进的神经网络,建立了油田产量预测的模型,并分析了各种参数对油田产量的影响。
油气田产量预测模型;神经网络算法;参数分析
近年来国内外学者应用神经网络方法对各种类型的预测问题开展了大量的研究[1-3]。文献[4]通过对影响产能的各种因素进行了综合分析,采用多元线性回归得出它们之间的关系式,从而反映了油层的产能情况,但油田产量与其影响因素不是简单的线性关系,而是复杂的非线性随机关系。本文通过对油井初期产量与油层物性实际资料进行分析和取样,对BP神经网络算法进行了改进,利用神经网络的非线性映射和泛化能力,通过训练,建立了油田产量预测模型,并为实际计算提供了一条有效的途径。
1 BP神经网络算法及改进
1.1 标准BP神经网络算法
标准BP算法是一种有导师指导的学习算法。该算法的学习过程由正向传播和反向传播两部分组成,在正向传播过程中,输入模式从输入层经过隐含层神经元的处理后,传向输出层,每一层神经元的状态只影响下一层神经元状态。如果在输出层得不到期望的输出,则转入反向传播,此时误差信号从输出层向输入层传播并沿途调整各层连接权值和阈值,以使误差不断减小,直至达到精度要求。该算法实际上是求误差函数的极小值,它通过多个样本的反复训练,采用梯度下降法使权值沿着误差函数负梯度方向改变,并收敛于最小点。
1.2 Levenberg-Marquardt算法
众所周知,梯度下降法最初下降较快,但随着接近最优值,由于梯度趋于零,致使误差函数下降缓慢,而牛顿法则可在最优值附近产生一个理想的搜索方向。Levenberg-Marquardt,实际上是梯度下降法和高斯牛顿法的结合,它的优点在于网络权值数目较小时收敛非常迅速。它比传统的BP及其他改进算法(如共轭梯度法,附加动量法,自适应调整法等)迭代次数少,收敛速度快,精度高[5]。
其基本思想是使每次迭代不再沿着单一的负梯度方向,而是允许误差沿着恶化的方向进行搜索,同时通过在最速梯度下降法和高斯牛顿法之间自适应调整来优化网络权值,使网络能够有效收敛,这样大大提高了网络的收敛速度和泛化能力。其权值调整公式为
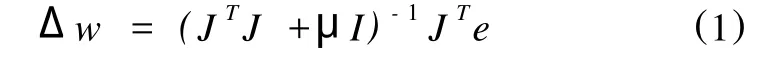
式中:e——误差向量,J——误差对权值微分的雅可比矩阵,μ——一个标量,当μ增加时,它接近于具有较小的学习速率的最速下降法,当μ下降到0时,该算法就变成高斯-牛顿法了。因此,L-M算法是在最速下降法和高斯-牛顿法之间的平滑调和。
1.2.1 L-M算法具体迭代步骤
(1)将所有输入送到网络并计算出结果,另用误差函数计算出所有目标的误差平方和。
(2)计算出误差对权值微分的雅可比矩阵。首先,定义Marquardt敏感度:

从(2)式可以看出,敏感度为误差函数E对m层输入的第i个元素变化的敏感性,其中,n为每层网络的加权和。敏感度的递推关系式为可见,敏感度可由最后一层通过网络被反向传播到第一层:
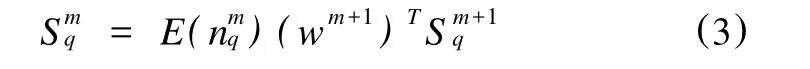

然后,用(4)计算雅可比矩阵的元素:

(3)用式(1)求出Δw。
(4)用w+Δw重复计算误差的平方和。如果新的和小于步骤(1)中的和,则用μ除以θ(θ>1),并有w=w+Δw,转向步骤(1),否则,用μ乘以θ,转向步骤(3)。当误差平方和减小到某一目标误差时,算法即被认为收敛。
2 建立预测模型
(1)输入参数的确定。输入参数的选取主要考虑油井初期产量的影响因素,同时还要考虑这些数据的可采集性。研究中选取了以下4个参数作为神经网络的输入:有效厚度、渗透率、孔隙度、含水饱和度。
(2)输出参数的确定。对于本研究而言,输出参数只有一个,即油井产量。
(3)网络层数的确定。由于只有一个隐含层的三层前向神经网络,且以任意精度逼近任意非线性映射的能力,所以本研究采用三层神经网络。
(4)激励函数的确定。激励函数是神经网络中极为重要的参数。在应用BP算法的多层前向网络中,采用的是Sigmoid函数。
(5)隐含层节点数的确定。隐含层神经元数代表网络输入与输出之间的非线性程度,对模型训练速度和预报能力有着重要影响。由于输入向量有4个元素,所以网络的输入层的神经元有4个,根据 Kolmogogorov定理知,网络中间层的神经元可取9个。
3 模型检验
考察安塞油田某区块的20口油井[4],选取其中15口油井的原始数据作为训练样本,另外选取5口油井作为测试数据。为了消除量纲的影响,对原始数据做归一化处理使其在区间[0,1]之间变化,研究采用的归一化公式为:
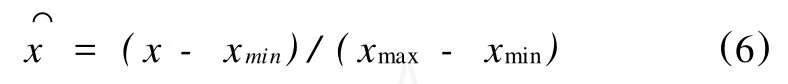
网络训练结束后,须对归一化的数据进行反归一化,得到实际数据。
利用Matlab编制程序[6],建立具有4个输入节点,9个隐层节点,1个输出节点的神经网络,精度选为0.001,训练步数定为2000,并对实际数据进行仿真,两种仿真结果见表1。从中可以看出,采用BP神经网络和L-M神经网络算法训练时,收敛速度都很快,比较而言,L-M神经网络算法,在网络训练和网络测试中的相对误差比BP神经网络算法误差要小。
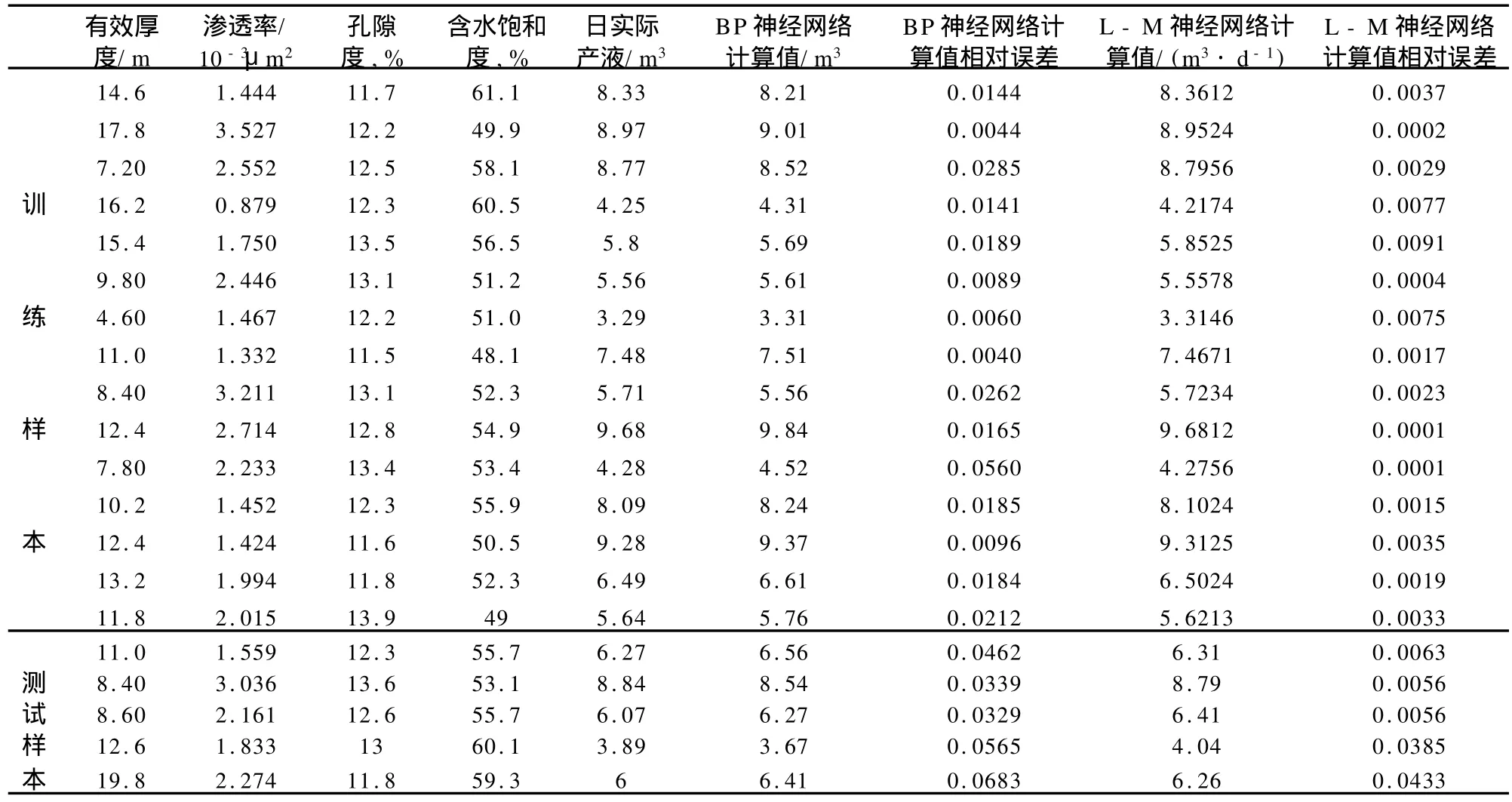
表1 油井初期产量的训练与预测
4 预测产量参数分析
选择前4个参数进行分析。利用训练好的LM神经网络模型,其他参数不变,只改变一个参数来分析对油井产量的影响[7]。
4.1 有效厚度对产量的影响
渗透率为2.1×10-3μm2,孔隙度为12.6%,含水饱和度为52.6%,有效厚度分别为4.6、4.8、5.8、6.4、6.8、7.2、7.6、8.4、9.6m。利用训练好的LM神经网络计算油井的产量,油井产量和有效厚度的关系曲线如图1,从中可以看出,在其他参数不变的情况下,有效厚度和产量之间的关系为非线性曲线,产量随着有效厚度的增加而增加。但当有效厚度过大时,它对产量的影响不是很显著。
4.2 渗透率对产量的影响
有效厚度为11.2m,孔隙度为12.3%,含水饱和度为55.7%,渗透率分别为1.332、1.467、1.559、1.699、1.836、2.161、2.331、2.446、2.795×10-3μm2。利用训练好的L-M神经网络计算油井的产量,油井产量和渗透率的关系曲线如图2,从中可以看出,在其他参数不变的情况下,有效厚度和产量之间的关系大致为线性的,产量随着渗透率的增加而增加。
4.3 孔隙度对产量的影响
有效厚度为 10.2m,渗透率为 1.559×10-3μm2,含水饱和度为57.9%,孔隙度分别为11.5%、11.8%、12.2%、12.5%、12.8%、13.1%、13.4%、13.6%、13.8%,利用训练好的L-M神经网络计算油井的产量,油井产量和渗透率的关系曲线如图3,从中可以看出,在其他参数不变的情况下,有效厚度和产量之间的关系大致为线性的。产量随着孔隙度的增加而减少。
4.4 含水饱和度对产量的影响
有效厚度为 11.8m,渗透率为 1.476×10-3μm2,孔隙度为13.7%,含水饱和度分别为50.1%、52.3%、53.1%、54.9%、55.7%、56.2%、58.1%、59.2%、60.5%,利用训练好的L-M神经网络计算油井的产量,油井产量和渗透率的关系曲线如图4,从中可以看出,在其他参数不变的情况下,含水饱和度和产量之间的关系为非线性曲线,产量随着含水饱和度的增加而减少。
5 结论
(1)采用改进的BP神经网络对油井产量进行预测,具有较高的精度。同时,该神经网络具有很好
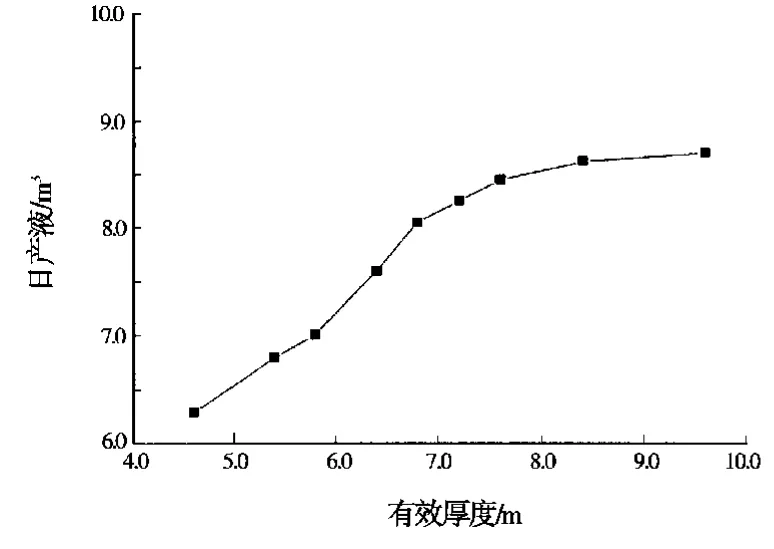
图1 有效厚度对产量的影响
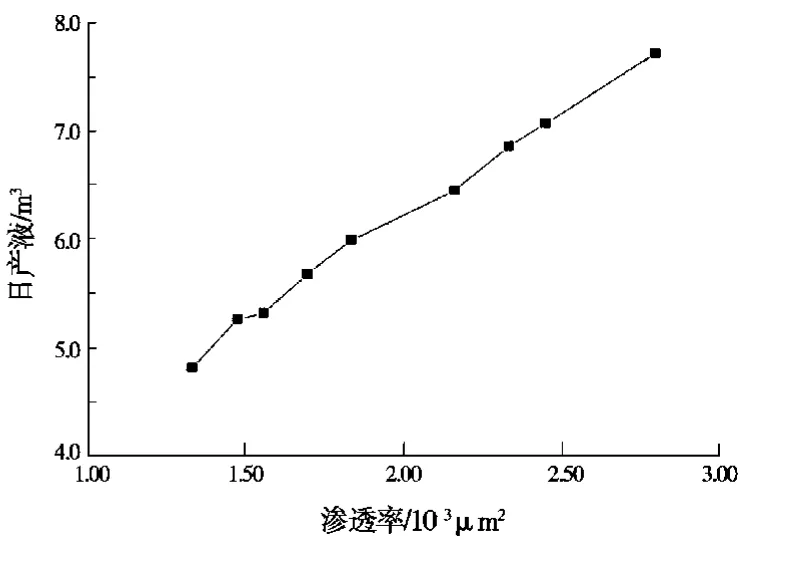
图2 渗透率对产量的影响
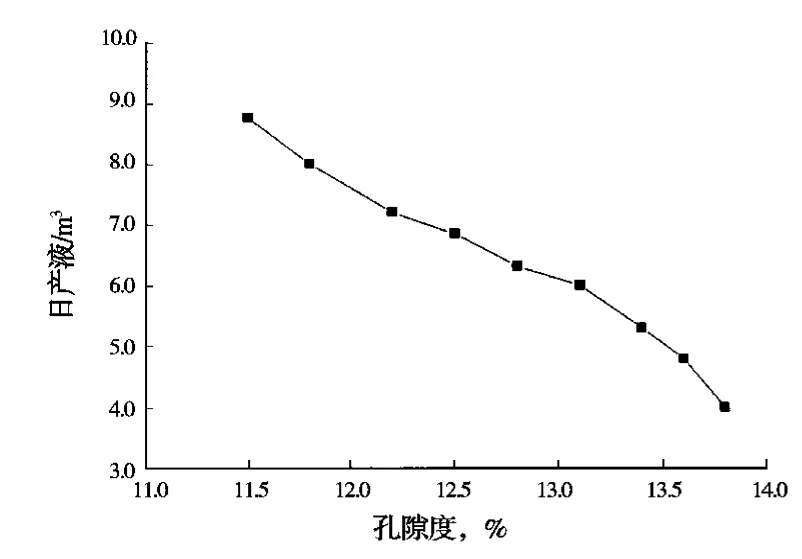
图3 孔隙度对产量的影响
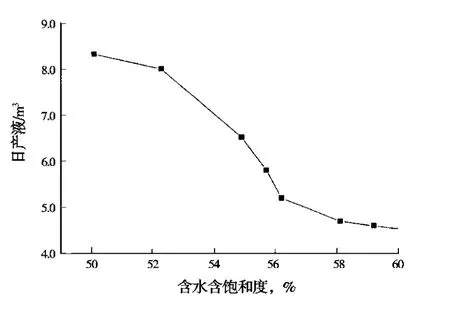
图4 含水饱和度对产量的影响
(2)各种参数对油井产量的影响规律不同。有效厚度、含水饱和度和油井产量的关系为非线性曲线;渗透率、孔隙度和油井产量的关系近似为线性关系。
(3)本研究是在一定的区块和地质背景下建立起来的,实用范围仅仅局限于此区块的勘探开发,而对于其他区块,还必须根据自身的地质背景,物性资料确定相应的神经网络模型,所以该模型的使用有一定的局限性。
[1]Chan W,T,chow Y K,liu L F.Neural network:an alternative to pile driving formulas[J].Computers and Geotechnics,1995,17(2):135-1561
[2]Lee I M,lee J H.Prediction of pile bearing capacity using artificialneuralnetworks[J].Computers and Geotechnics,1996,18(3):189-200
[3]王光兰.遗传算法在油田产量预报中的应用[J].西南石油学院学报,2000,22(2):34-35
[4]李栓豹,陈雷.多元线性回归在安塞油田产量预测中的应用[J].承德石油高等专科学校学报,2004,4(6):27-31
[5]马立平,仁宝生.油田产量灰色神经网络混合预测模型研究[J].石油天然气学报,2008,30(5):129-133
[6]张德丰.MATLAB神经网络应用设计[M].北京:机械工业出版社,2008:20-30
[7]陈铁冰.基于神经网络的混凝土预制桩单桩竖向极限承载力参数分析[J].公路交通科技,2007,24(11):87-91
编辑:刘洪树
TE318
A
1673-8217(2010)03-0053-03
2009-12-08;改回日期:2010-01-21
翟亮亮,讲师,1980年生,2008年毕业于西北大学应用数学专业,主要研究领域为数学物理反问题和测井方法。
