铣削加工表面轮廓的几何分形特征

淦，黄宜坚

（华侨大学机电及自动化学院，福建 泉州 362021）

铣削加工表面轮廓的几何分形特征

（华侨大学机电及自动化学院，福建 泉州 362021）

将分形几何学运用于铣削表面的形貌研究，分别采用结构函数法和重标极差分析法，计算出不同铣削表面的分形维数D和垂直尺度因子G.根据计算结果，运用改进Weierstrass-Mandelbrot分形函数模拟仿真出相应的表面轮廓，并画出实测表面轮廓和模拟表面轮廓的高度归一化概率密度分布图.试验结果表明，铣削表面轮廓分形维数D、垂直尺度因子G随着表面粗糙度的增加而降低；仿真出的表面轮廓和实测表面轮廓具有相同的高度归一化的概率密度分布，并能更加真实地反映出表面轮廓的细微结构.

分形几何；分维维数；垂直尺度系数；铣削；表面轮廓

随着几何分形学的发展和成熟，分形理论被广泛用于加工和磨损表面的形貌和粗糙度研究.它的引入为解决难以处理和准确表达的复杂表面形貌问题，提供了新的途径.相关文献表明［1-6］，表面形貌具有统计自相似和自仿射的分形特征.因此，从理论上讲是可以通过轮廓曲线的分形维数和形貌系数来表征加工表面的.El-Sonbaty等［7］用关联维数仿真的铣削加工表面的轮廓，与实测表面轮廓有着很好的吻合性.朱华等［8］运用形貌系数或特征粗糙度参数Ra＊来唯一表征粗糙表面，比单独运用分形维数D和垂直尺度系数G更能敏感地反映表面粗糙度地变化.本文运用结构函数法和重标极差分析法［9-11］，求出加工表面轮廓的分形参数，代入Weierstrass-Mandelbrot（W-M）分形轮廓仿真函数，绘制相应的表面轮廓，并与实测表面轮廓进行比较.

1 铣削加工表面轮廓的分形现象

1.1 分形证明

机械加工表面的微观显示出统计自相似性和自仿射性，据此，在不同的放大倍数下可以看到表面不断出现的相似结构.即当测量尺度减小时，可以看到更加精细的微观结构.换言之，机械加工表面具有明显的分形现象.

铣削试验中，试件实测表面轮廓在不同取样长度内的形貌，如图1所示.图1中：Z（x）为轮廓高度值；N为采样数据点.由图1可知，当铣削表面轮廓的分辨率不断提高（或者说观察尺度逐渐减小）时，可以看到轮廓表面会重复显现一定的微观精细结构.因此，铣削加工表面轮廓确实存在分形现象.

根据Lyanpunov分形指数（λ）的大小，也可以判断轮廓表面是否存在分形［12］.具体过程如下：将由粗糙表面轮廓测量仪所测的轮廓高度值Z（x）当作一维时间序列，然后将该时间序列输入到求解Lyanpunov指数的有关程序，得到Lyanpunov指数谱，如图2所示.图2中：τ为时延步长.根据图2，可计算出平均Lyanpunov指数λav=4.717 3＞0，由此可证明，铣削加工零件表面轮廓存在明显的分形现象.

再者，通过相空间重构动力学系统的奇异吸引子，也可辨识系统是否存在分形.如果系统具有分形性质，其最终运动归宿集中在奇怪吸引子上.在吸引域之外，系统运动不断向“吸引子”靠拢；而在吸引域之内，由于对初始条件的敏感依赖性，系统运动的轨道间互相排斥、折叠，充满了整个吸引域却又永不重复.具体过程如下：对所测表面轮廓数据时间序列Z（x）进行重构，通过观察重构的相空间轨迹是否存在奇异吸引子，若存在，则说明系统存在分形.铣削表面轮廓的相空间重构伪相图，如图3所示.从图3可知，铣削表面轮廓的相空间重构伪相图呈现一定的形状和轨迹.因此，铣削表面轮廓再一次被证明具有分形现象.

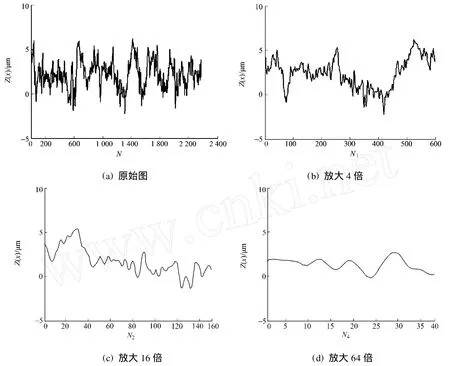
图1 铣削加工表面轮廓的自相似性和仿射性Fig.1 Self-similarity and self-affinity of the milled surface proflie

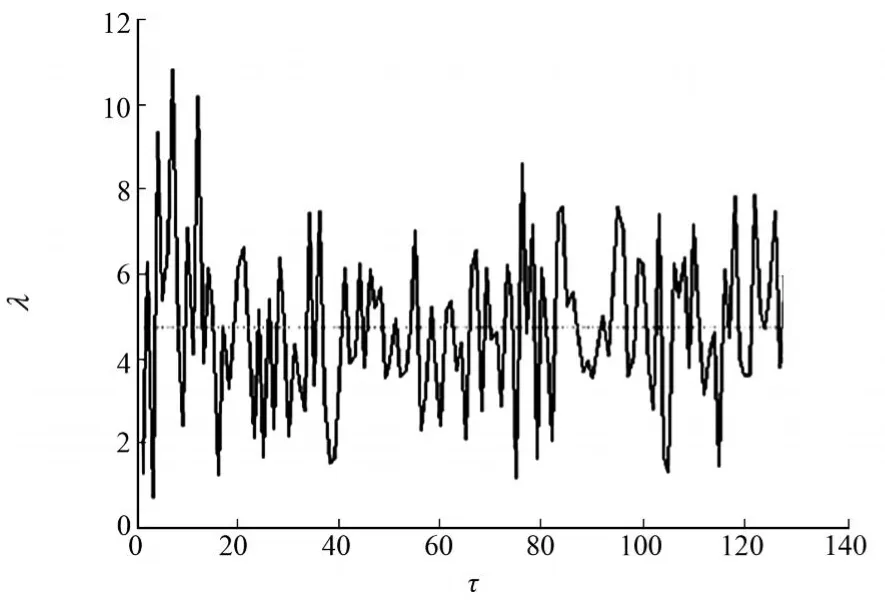
图2 铣削表面轮廓Lyanpunov指数图Fig.2 Lyapunov exponents diagram of milled surface profile

图3 相空间重构图Fig.3 Graph of reconstructed phase space

1.2 分形维数和垂直尺度的物理含义

铣削加工表面有着这样的特性：表面上幅值比较大的峰，其波长一般比幅值小的波峰要长；对于波谷也有同样的现象.因此，加工表面分形维数表达了表面所具有的复杂结构的多少和结构的微细程度，以及微细结构在整个表面中所占能量的相对大小.分形维数越大，表面中非规则的结构就越多，结构越精细，而精细结构所具有的能量相对越大.

依据Weierstrass-Mandelbort（W-M）分形函数，加工表面轮廓［7］可表示为

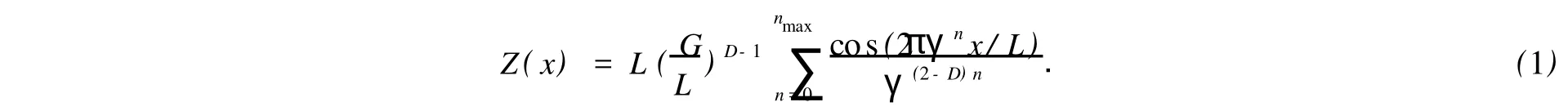
式（1）中：L为表面轮廓采样长度；x是采样长度在x上的坐标；γ为大于1的常数，取1.5为适宜的［10］，且空间频率的模γn=1/L，决定了轮廓的功率谱.式（1）为改进后的分形几何中的W-M函数，具有不可微、连续和自仿射性，而这正符合粗糙表面轮廓的数学特性.

若将轮廓高度值Z（x）归一化后，式（1）可改写为

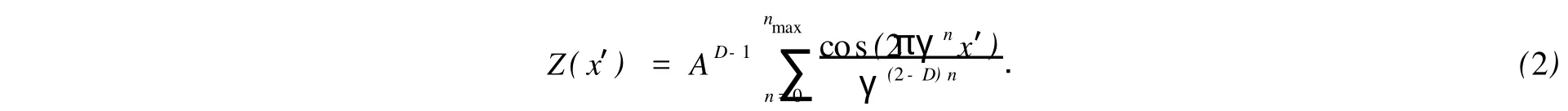
分形函数增量（或称轮廓高度差）Z（x+λ）′-Z（x′）服从期望为零的独立高斯分布，其方差为

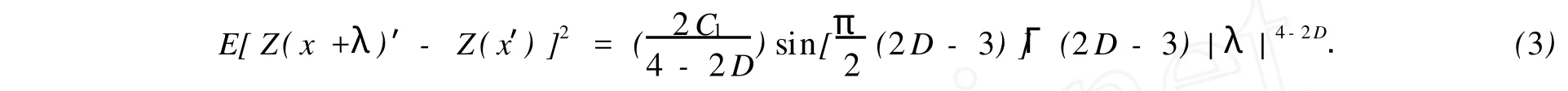
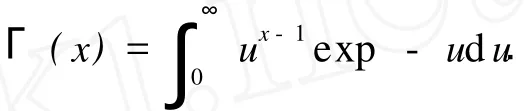
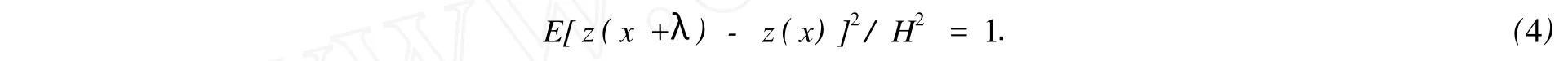
式（4）中：H就是z（x）的一个特征性的参数.式（4）可以改为

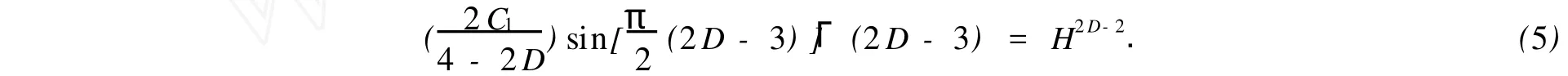
将式（5）代入式（4），可得

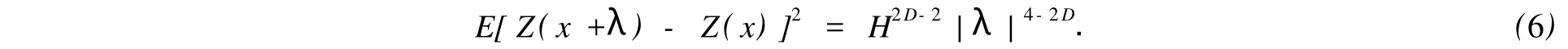
对于W-M函数，根据功率谱函数式，可以得到该函数的方差的期望为

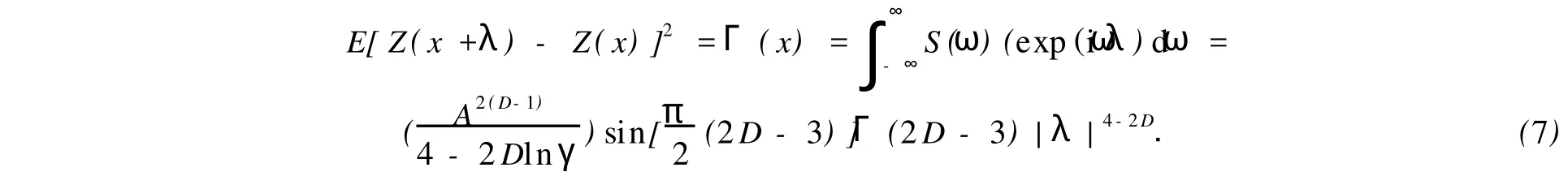
比较式（6），（7），可得

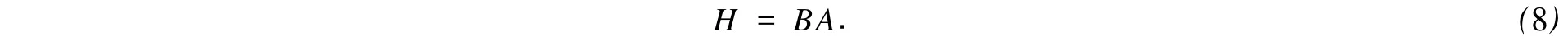
2 分形维数的计算方法

2.1 结构函数法

将铣削表面轮廓曲线看成一时间序列Z（x），由于其分形特性，使得该时间序列的采样数据的结构函数满足

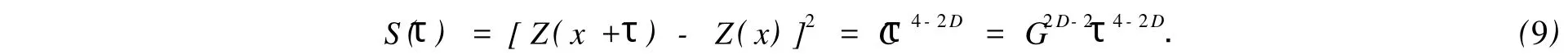
式（9）中：［Z（x+τ）-Z（x）］2为差方的算术平均值；τ为数据间隔的任意选择值；G为铣削表面轮廓的垂直尺度系数；D为轮廓曲线的分形维数.从式（9）还可看出，结构函数S（τ）与数据间隔成幂指数关系.

针对若干尺度τ对轮廓曲线的离散信号，计算出相应的S（τ），然后画出双对数logS-logτ图，如图4（a）所示.通过最小二乘法线性拟合出直线段，得到其斜率k和截距b.即有

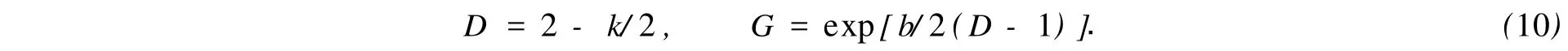
由式（10）可知，分形维数D和垂直尺度系数G是独立于数据间隔τ的，而且垂直尺度系数G与分形维数有关.这就说明了，分形轮廓主要取决于分形维数D，而两分形参数（D，G）可以表征铣削加工粗糙表面的固有本质规律.因此，该两分形参数可以完全表征铣削加工表面轮廓形状，具体的表面轮廓可由D，G分形参数值代到式（1）得到.

2.2 重标极差分析法

表面轮廓曲线可以用一维布朗函数来描述，它具有自放射性，其分维数D为

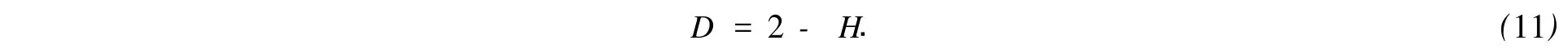
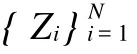
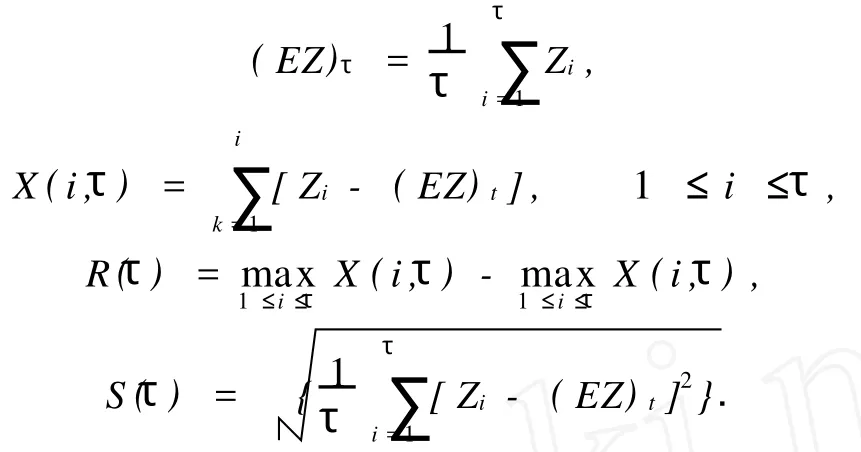
R（τ）/S（τ）与τH的关系为

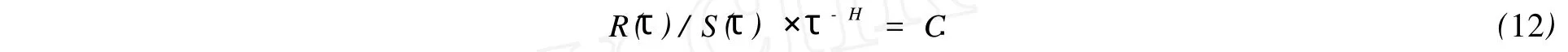
式（12）中：C为常数.计算出｛τ，R（τ）/S（τ）｝的值，在双对数坐标系｛lnτ，lnR（τ）/S（τ）｝中用最小二乘法拟合，如图4（b）所示.由图4（b）得到直线段斜率H，并通过计算得到轮廓曲线的分维数.

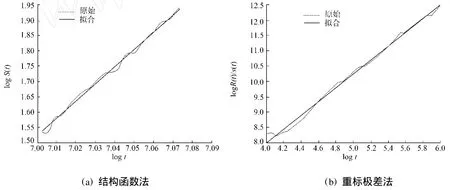
图4 表面轮廓的双对数图Fig.4 log-log graph of surface profile

3 粗糙度与分形参数的关系

对于式（1）的W-M分形函数，其均值和偏度分别为

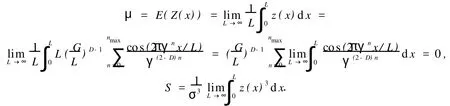
经过数值仿真发现，S≈0.因此，W-M分形函数是近似为零均值，服从对称分布的.由轮廓算术平均偏差Ra，也即粗糙度的定义可知

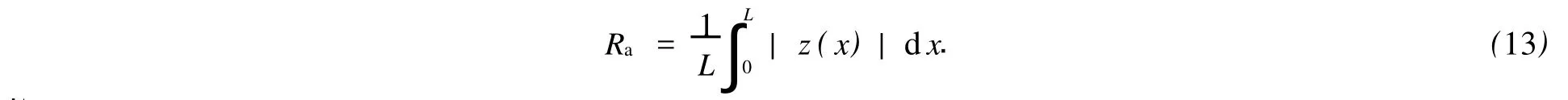
将分形函数式（1）代入式（13），则有

通过理论分析和数值模拟求证，找出分形参数D，G与粗糙度Ra的数值关系［14］为

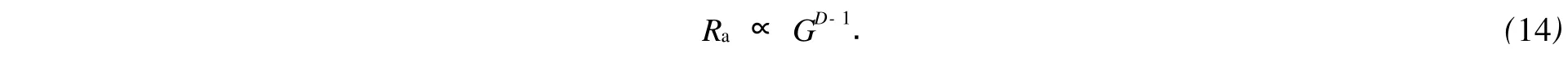
大量的计算和理论分析表明，G＜1且1＜D＜2.因此，从式（14）可知，粗糙度Ra与分形维数D存在幂指数关系，粗糙度Ra随着分形维数D上升而下降，减小而增大；而当分形维数D固定不变时（1＜D＜2），粗糙度Ra与垂直尺度系数G呈单调递增关系.即Ra随G增大而上升，降低而减少.

若垂直尺度系数不变时，当分形维数D增大，铣削表面轮廓的精细结构越来越精细，故而表面粗糙度Ra值减小；若分形维数D不变，当垂直尺度系数G增大，铣削表面轮廓在同一位置处高度值增大，也就是说表面质量越来越粗糙，从而表面粗糙度Ra上升.

4 实验部分

4.1 铣削实验

实验在数控铣床进行，共加工了6块45#钢，其粗糙表面质量分为6种不同等级.刀具选用型号为YT-08的硬质合金立铣刀，直径d为20mm高速螺旋齿（2齿，螺旋角为45°），加工过程不加铣削冷却液.相应粗糙表面的切削用量，如表1所示；铣削过程示意图，如图5所示.表1中：主轴转速为ω；进给量为F；切削深度为dp.

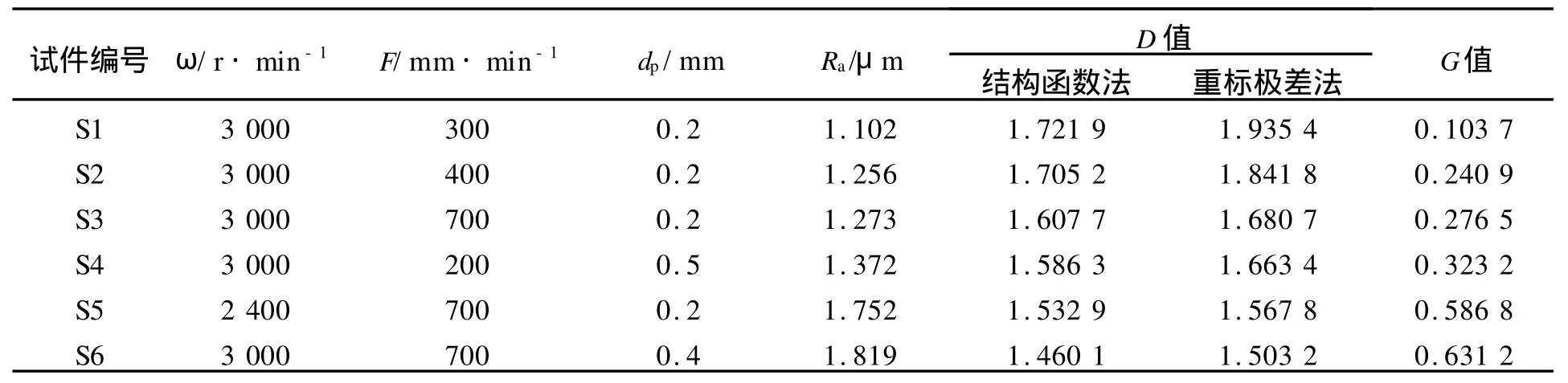
表1 试件切削参数值Tab.1 Specimen cutting parameters

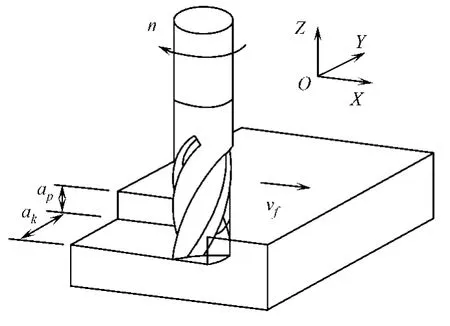
图5 铣削加工过程Fig.5 Milling process

试验的铣削加工零件表面粗糙度，由德国马尔XR200型针接触式粗糙度测量仪测量得到.该测量仪测针尖半径r=2μm，最小轮廓分辨率可达76nm，并配有专业的测量软件操作系统MarSurf XR 20.被测铣削表面轮廓的取样长度Lt=5.6mm，轮廓的采样点数NPT=11 200，分成7段，每段长度为0.8mm；软件评定长度L取中间5段，长度为4mm.通过软件分析可得表面轮廓粗糙度Ra，储存表面轮廓高度数据｛Zi｝iN=1，并运用上述两种分形维数计算方法，求得相应粗糙度表面下的分形维数D和垂直参考因子G.如表1所示.

从表1可看出，随着表面粗糙度Ra的不断增加，分形维数D单调递减，垂直尺度系数单调递增.这说明，加工表面轮廓的分形维数越高，垂直尺度系数越小，则铣削加工粗糙表面的精细结构相似程度越大，表面质量就越好，且轮廓平均峰值越小.Ra与分形参数属于单调关系，即证明了Ra∝GD-1表达式的准确性.另外一方面，对于相同的轮廓表面，运用结构函数法所计算出来的分形维数值要小于极差法所得分数维值.

4.2 加工表面轮廓的模拟仿真

通过两种分形维数计算方法，可求出分形参数D和表面粗糙度Ra.然后，将其代入W-M分形函数中，可得加工表面轮廓的形状.具体仿真流程如图6所示；铣削加工试件表面轮廓的实测和仿真对比，如图7所示；实测表面和模拟表面轮廓高度值归一化后，其概率分布图如图8所示.

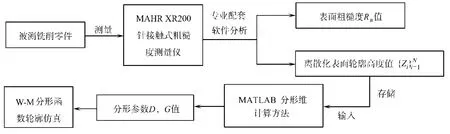
图6 加工表面轮廓模拟仿真流程分析图Fig.6 Process analysis flow for the simulation of machined surface profile

图7 试件表面轮廓的实测和仿真对比Fig.7 Comparison of the measured and simulated of specimen surface profile

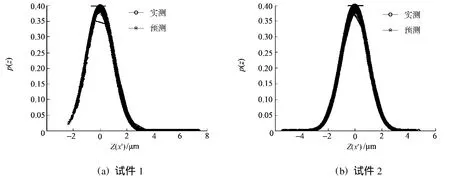
图8 试件表面轮廓高度值归一化后的概率分布图Fig.8 Plot of high degree of normalization probability density distribution of sample surface profile

5 结束语

通过改进的W-M分形函数仿真出的铣削加工模拟表面轮廓，与实测表面轮廓相比，其在统计规律上是具有相同的概率密度分布的.相对于实测表面，模拟表面能提供更多的细节信号，即能提供更多的精细结构.由于上述几何分形参数能够表征加工表面微观形貌的本身固有的规律，因而几何分形学同样可应用于其他机械加工表面的形貌描述和研究.

［1］MAJUMDAR A，BHUSHAN B.Role of fractal geometry in roughness characterizat ion and contact mechanics of surfaces［J］.ASME J Tribology，1990，112（1）：205-216.

［2］GAGNEPAIN J J，ROQUES-CARMES C.Fractal approach to two-dimensional and three-dimensional surface roughness［J］.Wear，1986，109（1）：119-126.

［3］ZHOU G Y，L EU M C.Fractal geometry model for wear prediction［J］.Wear，1993，170（1）：1-14.

［4］HASEGAWA M，LIU J C，OKUDA K，et al.Calculation of the fractal dimensions of machined surface profiles［J］.Wear，1996，192（1/2）：40-45.

［5］MAJUMDAR A，TIEN C L.Fractal characterization and simulation of rough surfaces［J］.Wear，1990，136（2）：313-327.

［6］JORDOM D L.Measurement and characterization of multiscale surfaces［J］.Wear，1986，109（1）：127-134.

［7］El-SONBATY I A，KHASHABA U A，SELMY A I，et al.Prediction of surface roughness profiles for milled surfaces using an artificial neural network and fractal geometry approach［J］.Journal of Materials Processing Technology，2008，200（1/2/3）：271-278.

［8］朱华，葛世荣，陈国安.磨合表面形貌变化的分形表征［J］.机械工程学报，2001，37（5）：68-71.

［9］葛世荣，索双富.表面轮廓分形维数计算方法的研究［J］.摩擦学学报，1997，17（4）：354-362.

［10］王建军，魏宗信.粗糙表面轮廓分形维数的计算方法［J］.工具技术，2006，40（8）：73-75.

［11］李成贵，刘杰.机械加工表面轮廓分形维数的两种计算方法［J］.航空精密制造技术，1997，33（4）：25-27.

［12］韩正铜，张永忠，黄民，等.磨削过程振动特征的实验研究［J］.制造技术与机床，2004（2）：63-65.

［13］费斌，王海容，蒋庄德.机械加工表面分形特性的研究［J］.西安交通大学学报，1998，32（5）：83-86.

［14］潘玉良，吴立群，张云电.分形模型参数与粗糙度参数Ra关系的研究［J］.中国工程科学，2004，6（5）：49-51.

Geometry Fractal Characteristics of Milled Surface Profiles

GAN Ben，HUAN G Yi-jian
（College of Mechanical Engineering and Automation，Huaqiao University，Quanzhou 362021，China）

The fractal geometry was used to investigate the microtopography of the milled surface.By use of the method of structural function and of rescaled range analysis，the fractal dimensionDand vertical scale coefficientGof the different milled surfaces can be obtained.According to the calculation results，the corresponding surface profiles are simulated by using the improved the Weierstrass-Mandelbrot fractal function and the graphs of high degree of normalization probability density distribution of the measured and simulated surface profiles are plotted.The experimental results have shown that the fractal dimensionDand vertical scale coefficientGof the milled surface profile decrease with the increase of roughness，the simulated and measured surface profiles have the same high degree of normalization probability density distribution and the former can reflect the fine structure of the surface profiles more really.

fractal geometry；fractal dimension；vertical scale coefficient；milling；surface profile

TH 161+.14；TG 54

A

1000-5013（2010）04-0371-07

（责任编辑：陈志贤 英文审校：郑亚青）

2009-04-24

黄宜坚（1945-），男，教授，主要从事机电系统设计与控制的研究.E-mail：yjhuang@hqu.edu.cn.

福建省高新技术开发研究计划重点项目（2005H035）；福建省自然科学基金计划资助项目（A0610020）