GPSD迭代法的收敛性定理

陈恒新

（华侨大学数学科学学院，福建 泉州 362021）

GPSD迭代法的收敛性定理

陈恒新

（华侨大学数学科学学院，福建 泉州 362021）

给出了一些易于检验的广义的预条件同时置换（GPSD）迭代法的收敛性定理.利用这些定理，能够较容易地判别解线性方程组Ax=f的GPSD迭代法的收敛性.数值例子证明，定理具有较好的实用价值.

线性方程组；GPSD迭代法；PSD迭代法；收敛性

广义的预条件同时置换（GPSD）迭代法包含了PSD迭代法，而PSD迭代法则包含了Jacobi超松弛迭代法（JOR），对称超松弛迭代法（SSOR），预优Jacobi迭代法（PJ）等迭代法［1-3］.文［1］在线性方程组系数矩阵A为相容次序矩阵及A的Jacobi迭代矩阵的特征值μj均为实数且＜1的条件下，证明了PSD迭代法收敛的充分必要性定理.文［2］在线性方程组系数矩阵A为对称正定矩阵或非奇异H-阵的情况下，研究了PSD迭代法的收敛性.本文对GPSD迭代法做进一步的研究，给出了一些易于检验的GPSD迭代法的收敛性定理.

1 GPSD迭代法

设A=D-E-F是n×n实矩阵.其中：D是非奇异对角阵；E是严格下三角阵；F是严格上三角阵.记L-D-1E，U=D-1F，对角矩阵Ω=diag（ω1，ω2，…，ωn）；T=diag（τ1，τ2，…，τn），τi≠0，i=1，…，n，则矩阵A的Jacobi迭代矩阵为B=D-1E+D-1F=L+U，且记B=［bi，j］.其中：bi，i=0，i=1，2，…，n.

求解线性代数方程组

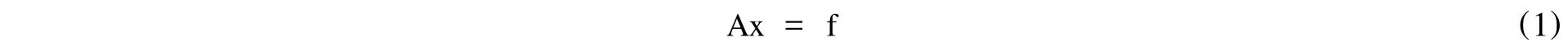
的GPSD迭代法为

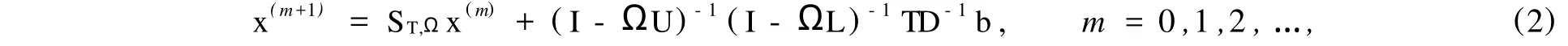
其GPSD法迭代矩阵为

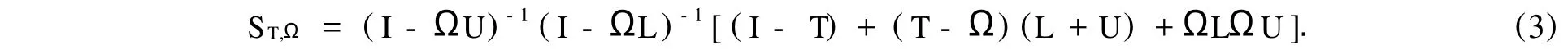
当取T=τI，Ω=ωI时，GPSD迭代法便成为PSD迭代法［1］.

为了叙述方便，引入如下记法：

（1）记Jacobi迭代矩阵B=［bi，j］，空集为φ，N1⊕N2=1⊕2=N=｛1，2，…，n｝，且N1∩N2=φ，1∩2=φ.

（4）集合K-L=｛i|i∈K而i∉L，对任一n阶方阵G=［gi，j］，|G|=［|gi，j|］.

需要说明的是，文中所取数集N1，1，N2，2皆非空.

2 非负矩阵的性质

定义1 对于n×n实矩阵G，M及N，如果M非奇异，并且有M-1≥0和N≥0，则称G=M-N为矩阵G的正规分裂.由文［4］定理3.8，定理3.13可得引理1，2.

引理1 设n×n矩阵G≥0，则I-G非奇异且（I-G）-1≥0的充要条件是ρ（G）＜1.

引理2 设G=M-N为矩阵G的正规分裂，且G-1≥0，则ρ（M-1N）＜1.

引理3［5］若A，B为n阶方阵，且|B|≤A，则ρ（B）≤ρ（A）.

3 GPSD迭代法的收敛性定理

定理1 设线性方程组（1）的系数矩阵A为非奇异H-矩阵，则当

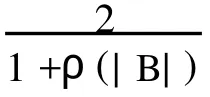
证明 因为A为非奇异H-矩阵，则有ρ（|B|）＜1，其中|B|=|L|+|U|.又因为U为严格上三角矩阵，Ω=diag（ω1，ω2…，ωn）≥0，所以有ρ（ΩU）=0ρ，（Ω|U|）=0.于是有

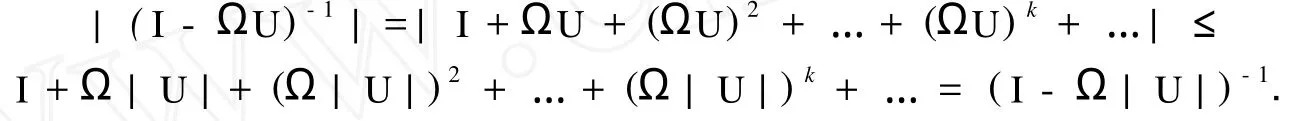
同理，因L为严格下三角矩阵，故有

|（I-ΩL）-1|≤（I-Ω|L|）-1.

于是有

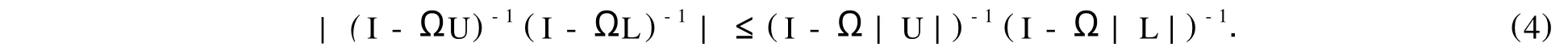
现记

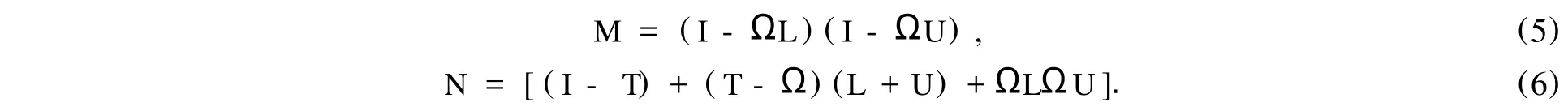
由式（3）可知

令

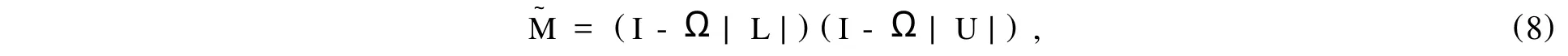
则由式（4），（5）有

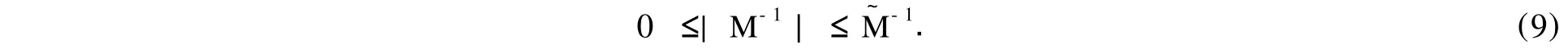
（i）当0＜τi≤1，i=1，2，…，n时，因0≤ωi≤τi，i=1，2，…，n，令

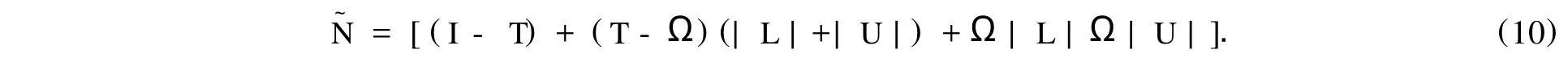
由于 I-T=diag（1-τ1，1-τ2，…，1-τn）≥0，T-Ω=diag（τ1-ω1，τ2-ω2，…，τn-ωn）≥0，故可知≥0，则有

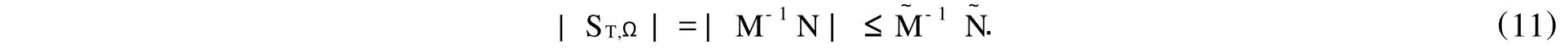
因为|B|≥0ρ，（|B|）＜1，0＜τi≤1，i=1，2，…，n.

所以，由式（11），（12）并据引理3可得

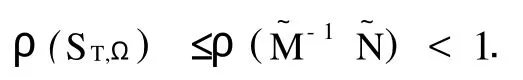
即GPSD迭代法收敛.

由式（6），（13）可知

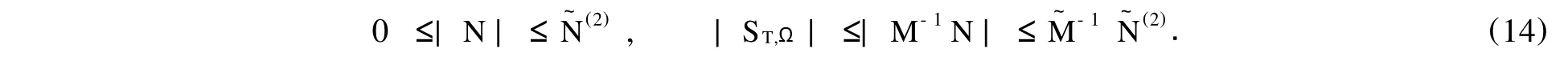
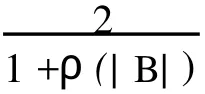
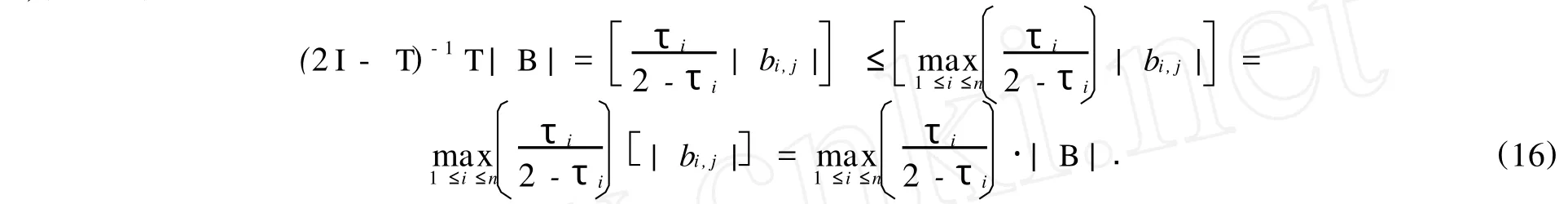
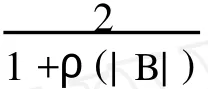
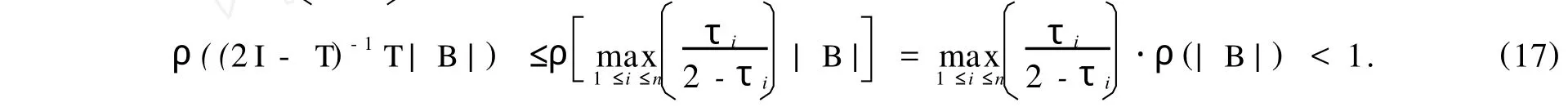
于是，由式（15），（17）并据引理1可知

（G（2））-1=（I-（2I-T）-1T|B|）-1（2I-T）-1≥0.

再由引理2可得

所以，由式（14），（18）并据引理3可得

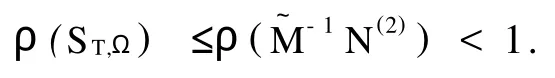
此时，GPSD迭代法也收敛.证毕.

引理4 对于任意的i∈N1，j∈N2，若i，j∈N-，则恒成立

ri，j=αi+βj+αβji-αβij＜1.

证明 因为i，j∈N-，所以有αi+βi=bi＜1，αj+βj=bj＜1，则有0≤βi＜1-αi和0≤αj＜1-βj.于是有αβji＜（1-αi）（1-βj），从而有

ri，j=αi+βj+αβji-αβij＜1.

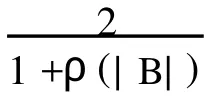
注1 因定理2（以及定理3）中N1（或1）可在N-（或-）中任取，所以该定理的应用性较广.

证明 若N1=N-，则N2=N+；若N1≠N-，则N2-N+≠φ.因为i∈N1⊂N-，对j∈N2-N+，有bj＜1，即j∈N-.由引理4可知，ri，j＜1.

据此及定理条件，可知对一切i∈N1，j∈N2，有ri，j=αi+βj+αβji-αβij＜1恒成立.所以可得

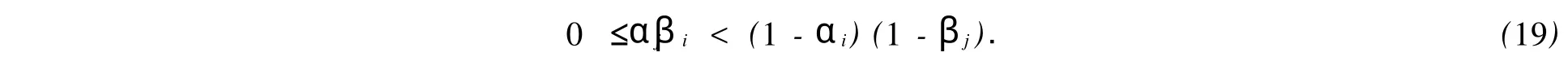
又由αi+βi=bi＜1，可得

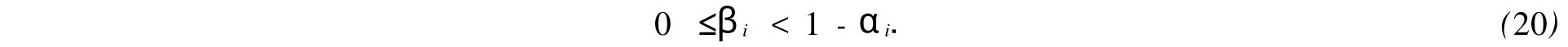
由式（19），（20）可知，1-βj＞0.因此，βj＜1.

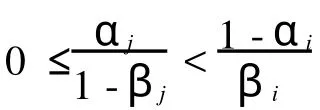
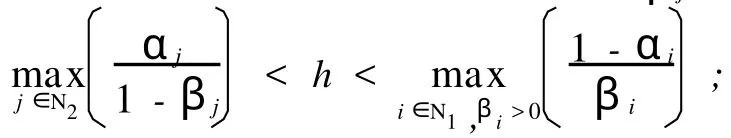
否则，｛i|βi＞0，i∈N1｝≠φ，即βi≡0，i∈N1，则取

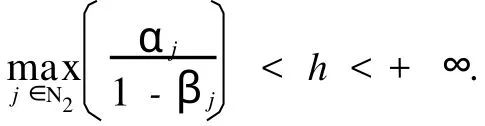
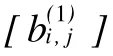
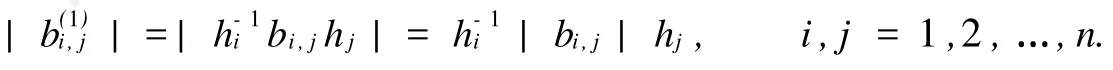
即|B1|=H-1|B|H，则ρ（|B1|）=ρ（|B|）.

因此，有ρ（|B|）＜1，即矩阵A为非奇异H-矩阵.所以，由定理1可知，当

时，解方程组（1）的GPSD迭代法（2）收敛.同理，对列也有如下相应定理.

定理3 在线性方程组（1）矩阵A的Jacobi迭代矩阵B中任取一1⊂-.如果对i∈1，j∈+，成立，则当0＜τi＜，0≤ωi≤τi，i=1，2，…，n时，解方程组（1）的GPSD迭代法（2）收敛.它隐含PSD（0＜τ＜，0≤ω≤τ），SSOR（0＜ω＜2），JOR（0＜τ＜），PJ（0＜ω≤1）等迭代法收敛.

4 数值例子

因为b1=0.6＜1，b2=1.2＞1，b3=1.125＞1，所以N-=｛1｝，N+=｛2，3｝.现取N1=N-则N2=N+，且有α1=0，β1=0.6；α2=0.7，β2=0.5；α3=0.5，β3=0.625.因为对i∈N1=｛1｝，j∈N+=｛3，4｝，有r1，2=0.5+0.7×0.6=0.92＜1，和r1，3=0.625+0.5×0.6=0.925＜1成立

因为b1=0.6＜1，b2=0.95＜1，b3=1.2＞1，b4=1.1＞1，所以N-=｛1，2｝，N+=｛2，3｝.又因=1.45＞1，=0.9＜1，=0.6＜1，=0.9＜1，所以=｛2，3，4｝，+=｛1｝.

若直接取N1=N-，N2=N+，因r2，3=0.45+0.5+07×0.5-0.45×0.5=1.075＞1；若取1=，因=0.5+1.45×0.4=1.08＞1.所以，不能用文中定理判别解该方程组之GPSD法的收敛性.但是，由于文中定理的1（或1），可在-（或-）中任取，所以其应用性较广.如在例2中，可取N1=｛1｝⊂N-，则N2=｛2，3，4｝，α1=0，β1=0.6；α3=0.6，β3=0.6；α4=0.4，β4=0.7.

于是，对于i∈N1=｛1｝，j∈N+=｛3，4｝，则有r1，3=0.6+0.6×0.6=0.96＜1和r1，4=0.7+0.4×0.6=0.94＜1成立.

［1］陈恒新.关于PSD迭代法收敛的充分必要性定理［J］.应用数学与计算数学学报，1999，13（1）：11-20.

［2］刘兴平.某些迭代方法的收敛性［J］.数值计算与计算机应用，1992，13（1）：58-64.

［3］陈恒新.关于SSOR迭代法和Jacobi迭代法的敛散性［J］.华侨大学学报：自然科学版，1993，14（1）：20-26.

［4］瓦格RS.矩阵迭代分析［M］.蒋尔雄，等译.上海：上海科学技术出版社，1966：41-130.

［5］胡家赣.线性代数方程组的迭代解法［M］.北京：科学出版社，1997：18-19.

Convergence Theorem of GPSD lterative Method

CHEN Heng-xin
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

Some convergence theorems of GPSD（generalized preconditioned simultaneous displacement）iterative method are obtained in this paper.The convergence of GPSD iterative method for solving linear equationsAx=fcan be easily discriminated by use of these theorems.Two numericial examples are given，that shows these theorems had a good practical value.

linear equations；GPSD iterative method；PSD iterative method；convergence

O 241.6

A

1000-5013（2010）06-0706-05

（责任编辑：陈志贤 英文审校：张金顺，黄心中）

2009-12-16

陈恒新（1956-），男，副教授，主要从事计算数学的研究.E-mail：chenhx@hqu.edu.cn.

福建省自然科学基金计划资助项目（S0650018）