动态规划法在边坡工程稳定分析中的应用研究
2010-08-30林义国黄少敏
林义国, 黄少敏
(1.福建江河电气化公司,福建 福州 350001;2.福建水利电力职业技术学院,福建 永安 366000)
1 前言
边坡是人类生存的重要环境,甚至是工程建筑的重要组成部分。在水利水电工程建设中,也经常遇到边坡稳定问题。传统上,对边坡工程的稳定分析多数采用极限平衡理论方法,但是极限平衡理论方法一般都引入较多的假定条件,因此分析的结果往往与实际情况并不十分吻合。随着计算机软件、硬件的飞速发展,采用理论体系更为严格的方法进行边坡稳定分析已经成为可能。有限单元法全面满足了静力许可、应变相容和应力、应变之间的本构关系[1],因此可较为理想地分析边坡稳定的应力、变形和稳定性。但是如何利用有限元的计算结果,确定安全系数和临界滑动面,这是很有意义的工作,各国专家学者对此进行了大量的研究分析,取得了很多研究成果,也推动了边坡工程稳定性研究理论和方法的发展。
在利用有限元应力场搜索临界滑裂面的工作中,许多学者都做了有益的尝试。John Krahn 2004年直接沿用条分法中使用的搜索方法,假设滑移面的形状,并采用试算或其它优化算法搜索临界滑移面[2]。Giam和Donald 1988年提出一种由已知的应力场确定临界滑移面及最小安全系数的方法,称为模式搜索(CRISS)法,它根据有限元计算得到的应力场,由应力水平较高点出发,形成一个由坡顶到坡底的破坏面[1]。另外还有许多不同的方法,由于不同的边坡稳定研究方法具有不同的优缺点,适用于不同的工程地质环境,因此为促进边坡研究新方法的出现和传统方法的改进与发展。本文在前人研究的基础上,尝试利用有限元法计算结果,在已知边坡应力场的情况下,引入动态规划法搜索边坡的最危险滑动面位置,并求出最小安全系数进行边坡工程的稳定分析研究。
2 动态规划法确定滑动面基本原理[3]
2.1 安全系数F的定义
采用公式(1)的形式,如下所示:
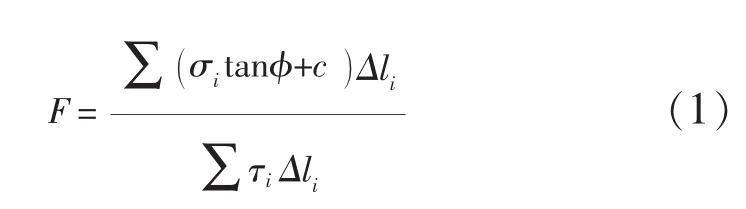
式中:σ是滑移面上一点的法向应力,τ是滑移面上一点的切向应力,c是粘聚力,准是内摩擦角,△li是滑移面上一段的长度。
2.2 动态规划法确定危险滑动面
动态规划是运筹学的一个分支,是求解决策过程最优化的数学方法。20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程的优化问题时,提出了著名的最优化原理,把多阶段过程转化为一系列单阶段问题,逐个求解,并创立了解决这类过程优化问题的新方法—动态规划。应用于边坡稳定分析时,主要思路是通过引入辅助函数G:

式中:Ri是滑移线上第i段的抗滑力,Si是滑移线上第段的滑动力。
动态规划可以找到一条路径,这条路径作为滑移面,使得目标函数公式 (2)取得最小值。计算是一个迭代过程,第一步需要假定安全系数,找到滑移面后更新安全系数F,然后重新搜索新的滑移面,直到前后两次安全系数的差值小于设定的阀值,迭代终止,一般迭代次数不会超过5次就会收敛[4-5]。
计算简图如图1所示,图中搜索网格的竖格线代表不同的搜索阶段 (Stage),横格线代表不同的搜索状态(State)。当搜索网格足够密时,就可以给出足够准确、光滑的滑移面。具体的搜索步骤如下:
定义优化函数为 Hi(j):初始阶段到点(i, j)—i阶段、状态的辅助函数G的最小值。则点(i+1,k)的优化函数可定义为:
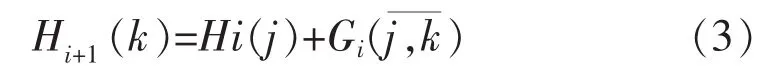


终结阶段的优化函数:
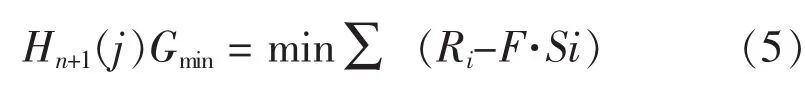
终结阶段的最优点就是满足hn+1(k)=minhn+1(j)的点,根据公式(5)可知,在从初始阶段任意点到终结状态任意点的所有路径中,只有以点(n+1,k)为终点的某条路径可以使G取到最小值。知道了终结阶段的最优点,根据公式 (3)就可以回溯得到上一阶段的最优点,逐步回溯至初始阶段,也就得到了使G取到最小值的那条最优路径。
这种方法不需要假设滑移面的形状,几次迭代搜索后可以自动找出临界滑移面。为了求得滑移面的起点和终点,需在实际土坡范围外设置虚拟计算单元,需要另外建立搜索网格。同时需要判断搜索网格中节点所在的单元,并插值得到这些节点的应力。
3 算例分析
本算例是一个均质黏土边坡,取自RockScience公司的软件算例,断面几何尺寸及力学计算参数。如图2所示 (作为算例验证分析,可采用非实际工程的边坡,这个算例在多篇文献中均有采用)。
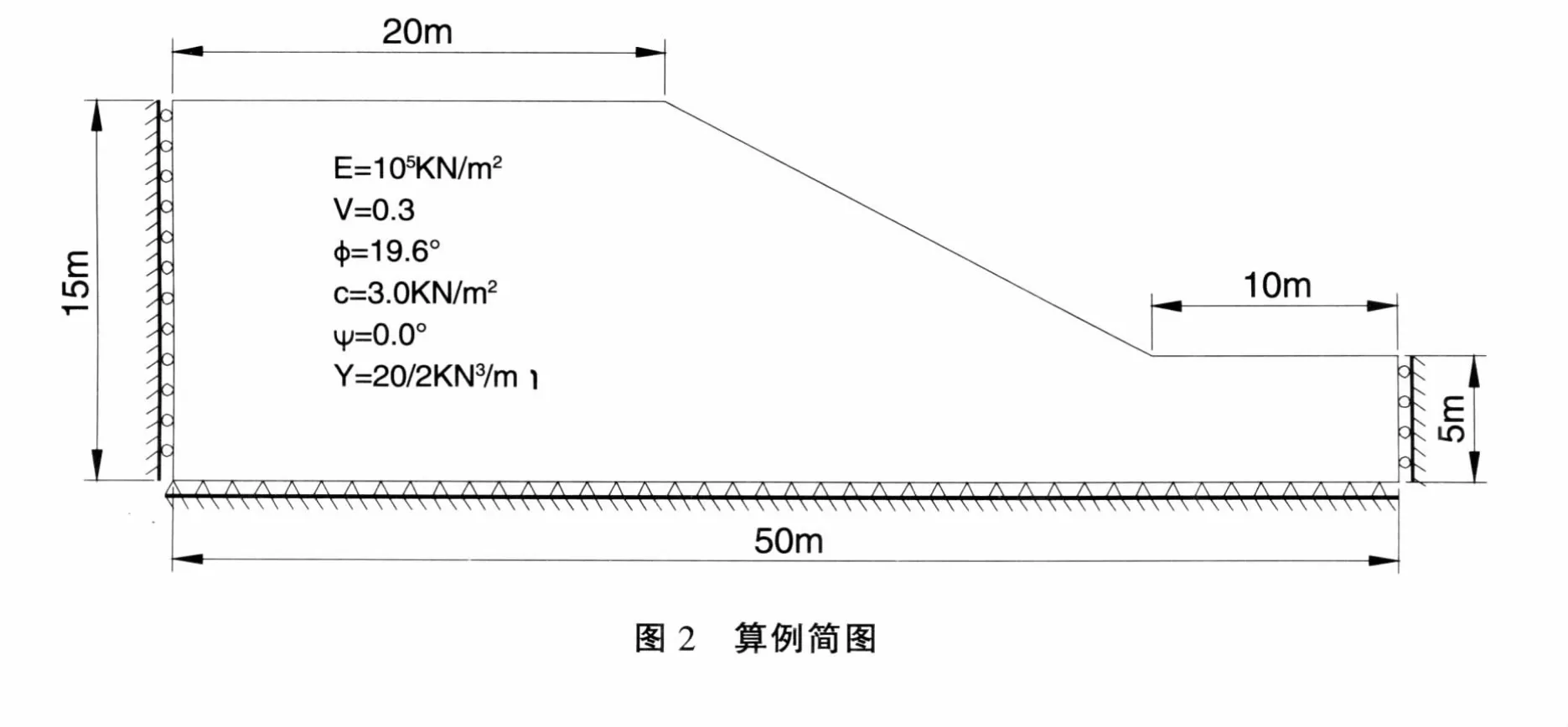
3.1 网格剖分
有限元计算的网格剖分如图所示,边界条件如图2所示,左侧和右侧边界为滑动支座,约束x方向位移,下方为固定支座,约束x和y两个方向的位移。
3.2 计算结果
本文方法计算的安全系数为1.13,应力及变形结果云图见图4、图5给出了根据有限元计算出的应力场自动搜索出的临界滑移面,迭代3次得到。

图3 网格剖分
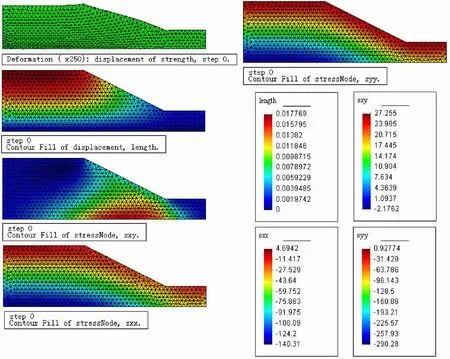
图4 有限元计算结果
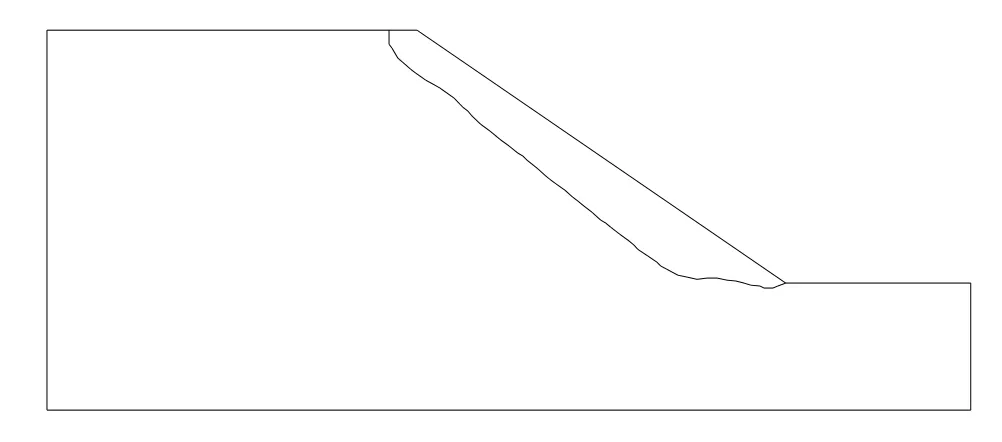
图5 临界滑移面
3.3 各种方法计算比较
图6是本算例的Bishop解的临界滑移面,其它方法得到的滑移面类似。表1列出了各种方法得到的安全系数 (本算例的极限平衡法结果均采用RockScience公司的Slide软件计算得到的)。

图6 Bishop解的临界滑移面
4 结论
通过以上计算和比较,可以得出以下结论:
(1)应用本文方法确定边坡临界滑移面,与传统极限方法Bishop解确定的临界滑移面 (图6)十分相似,说明利用该方法分析边坡稳定是可行的,同时有限元方法可较为理想地分析边坡稳定的应力、变形和稳定性,弥补了极限方法的不足。
(2)本文方法计算得到的安全系数为1.13,稍稍大于极限方法所得的安全系数值 (表1中所示,如Bishop解的安全系数为0.987)。这表明并验证了传统极限方法计算的安全系数偏于保守的规律。
(3)用动态规划法确定边坡临界滑移面,不需要假设滑移面的形状,几次迭代搜索后就可以自动找出临界滑移面,大大减少了试算工作量,是边坡稳定分析方法的进步。

表1 条分法结果
[1]陈祖煜.土质边坡稳定分析—原理·方法·程序,北京:中国水利水电出版社,2003.
[2]John Krahn.2004.GeoSlope SlopeW Engineering Book.
[3]Ha.T.V.Pham,Delwyn G.Fredlund.2003.The application of dynamic programming to slope stability analysis.Can.Geotech.J.40:830-847.
[4]Jin-Zhang Zou,David J.Williams Wen-Lin Xiong.1995.Search for critical slip surfaces based on finite element method.Can.Geotech.J.32:233-246.
[5]Da-Yong Zhu.2001.A method for locating critical slip surfaces in slope stability analysis.Can.Geotech.J.38:328-337.
