基于我国全球连续监测与评估系统的ERP测定的精度分析

何战科,李志刚,杨旭海,程宗颐

(1.中国科学院国家授时中心,陕西西安710600;2.中国科学院精密导航定位与定时技术重点实验室,陕西西安710600;3.中国科学院上海天文台,上海200030)

0 引 言

地球自转参数(Earth Rotation Parameters,简写为ERP)是指极移和日长变化,这些参数決定着地面观测站在空间的精确位置以及地球坐标系在空间的指向。它与岁差、章动一起构成地球定向参数(Earth Orientation Parameters,简写为 EOP),它是实现天球参考架与地球参考架相互转换的最基本的参数。人造卫星和宇宙飞行器的精密定轨和导航都需要高精度的地球自转参数,因此,对地球自转参数的研究具有非常重要的意义。

COMPASS全球连续监测与评估系统是COMPASS卫星导航系统的重要组成部分,系统包括跟踪站、数据中心和分析中心等部分。其功能与国际GNSS服务(International Global Navigation Satellite System(GNSS)Service,缩写为IGS)相当。

随着经济建设和国防建设的发展,自主解算与预报地球自转参数已经变得越来越迫切。因此,基于我国完全自主的全球连续监测与评估系统,提供高精度、高分辨率的地球自转参数服务,为我国卫星导航系统的建设、发展和应用提供支撑服务。

1 地球自转参数变化概况

极移包括两个主要的周期成分[1]:一个是大约435天(1.2年)钱德勒周期,另一个是周年周期,极移的周年成分主要是由大气作用引起的受迫摆动。2000年-2009年期间极移变化如图1[1]所示。地球自转确定的日长(修正了潮汐改正)变化有几个毫秒,图2[1]给出了1973年-2009年期间的日长变化。

2 地球自转参数的估算

GAMIT[2-3]采用双差载波相位观测量作为基本观测量,处理时间随着站数的增加呈几何级数增加,如果按照IGS各分析中心采用两百多个站,以我们所用的计算机硬件条件,解算一个ERP结果至少需要两天时间,在本例中每解算一次也需要8 h左右。由于现有计算机硬件条件的限制,从目前的302个IGS05参考框架站中优选了22个站,这22个站构成的网几何分布良好、资料稳定:大部分站在ITRF2005框架中的坐标中误差都在1 mm以下,速度场中误差都在0.3 mm/y以下,分布图如图3(红五星★表示所选站)所示。仅三个站的中误差较大:ASPA站在X方向的坐标中误差为4 mm,速度场中误差0.8 mm/y;BILI站在Z方向的坐标中误差为3 mm,速度场中误差0.5 mm/y;GLPS站在Y方向的坐标中误差为2 mm,速度场中误差0.4 mm/y。

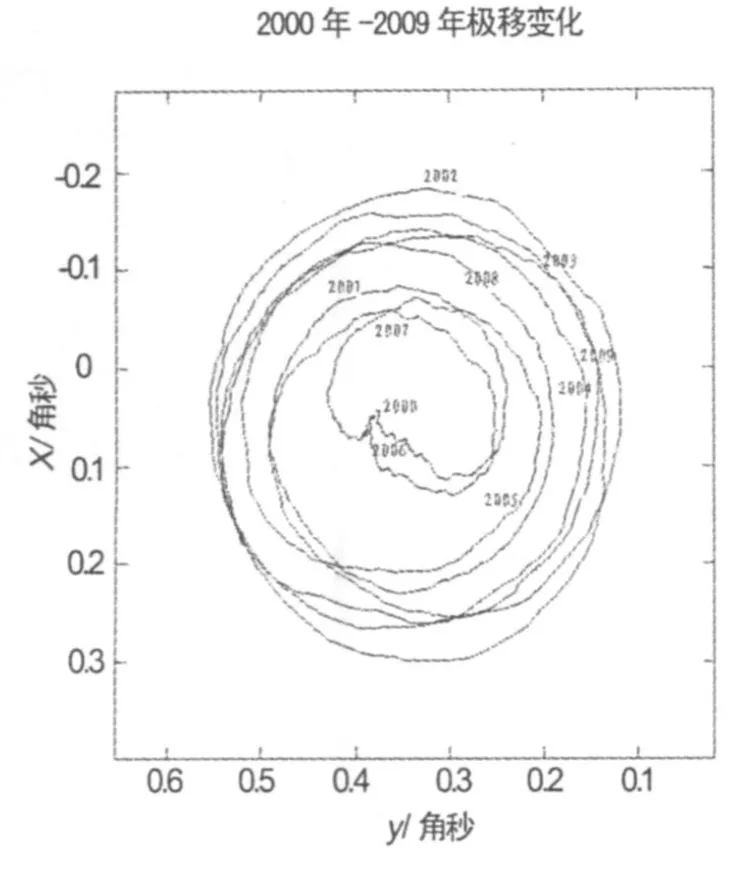
图1 2000年-2009年极移变化

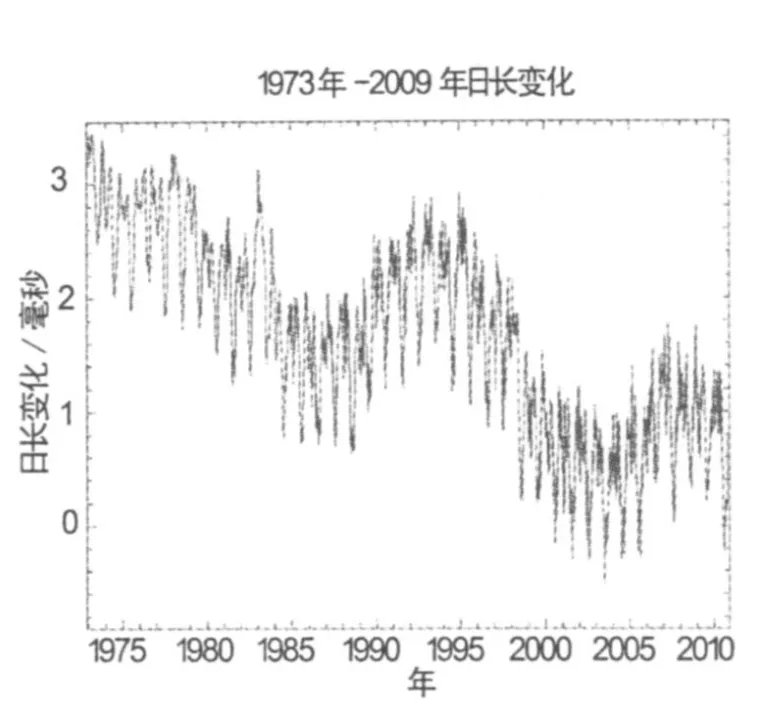
图2 1973年-2009年日长变化

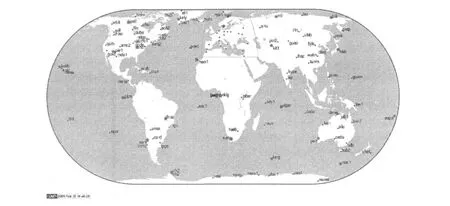
图3 选择的22个 IGS站分布图

3 分析与讨论

利用每24 h的数据估计数据段中点时刻的地球自转参数。估计了每日UTC 0时的地球自转参数[4-5](本例结果以下用NTSC_A表示用全球均匀分布的22个站数据的解算结果),经过剔除异常值及参数转换后[6],与IERS C04(UTC 0 h)同时刻的值进行了比较。IERS提供每日UTC 0 h时刻的地球自转参数,时间分辨率为1天。

3.1 NTSC_A与 IERS C04比较

利用优选的全球均匀分布的22个IGS站的数据,解算出2007年9月10日至10月26日期间经剔除异常值及参数转换后的结果减去IERS C04系列中的地球自转参数之差值,如图4～图6所示。

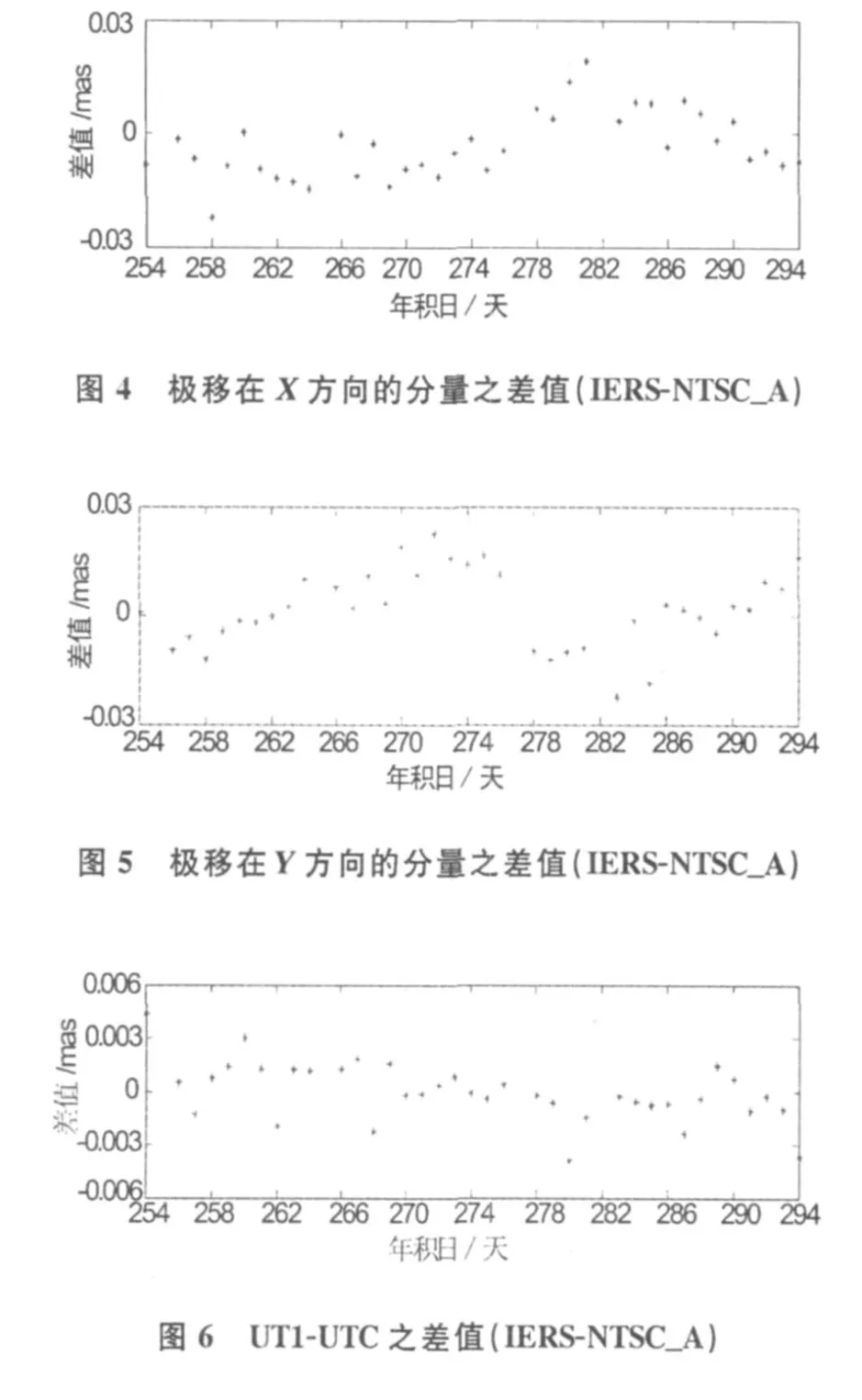
3.2 NTSC_A精度分析

NTSC_A与IERS C04的差值的标准差分别为:0.0065 mas、0.0109 mas、0.0013 mas,差值均方根 RMS分别为 0.0203 mas、0.0354 mas、0.0016 mas。这与IERS目前的精度相当。

3.3 目前全球连续监测与评估系统布网情况

目前,全球连续监测与评估系统跟踪网仅有5个国内核心站和一个海外站,选取国内的4个站和1个南极站附近的IGS跟踪站,为了构成几何分布更好的网,增加了3个将来可能布设全球连续监测与评估系统跟踪站附近的海外IGS站(北美、欧洲和南极各1个站),其中6个站在ITRF2005框架中的坐标中误差都在1 mm以下,速度场中误差都在0.4 mm/y以下,另外两个站在IT RF2005框架中的坐标中误差在4 mm以下,速度场中误差在0.9 mm/y以下。

利用这8个IGS跟踪站的数据,解算出2007年9月10日至9月29日期间经剔除异常值及参数转换后的结果(本例结果以下用NTSC_B表示用这8个站数据的解算结果)减去IERS C04系列中的地球自转参数之差值,如图7～图9所示。

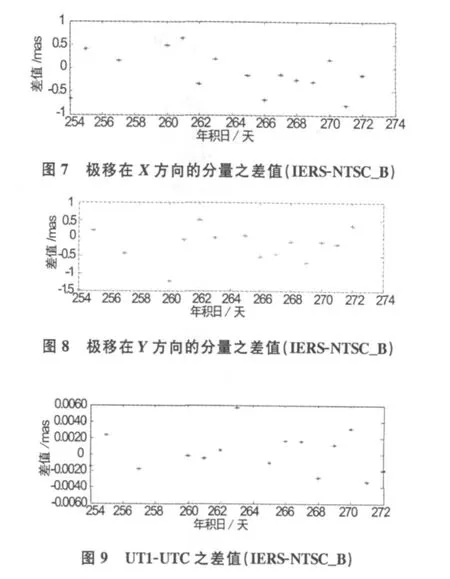
3.4 NTSC_B精度分析

NTSC_B与IERS C04的差值的标准差分别为:3.3892 mas 、0.8984 mas、0.0038 mas,差值均方根 RMS 分别为3.5328、0.8804、0.0042;显然,NTSC_B差值偏大。原因是台站几何分布问题,因此,要独立解算精度较理想的地球自转参数必须构建更合理的全球连续监测与评估系统网。

3.5 联合解算建议

由于GPS和GLONASS卫星导航系统具有不同的轨道交角,联合解算ERP的精度优于单系统解[7],表1[8]给出不同方案解算的 ERP系列与IERS Bulletin A系列的差值的均方根。因此,COMPASS 与GPS、GLONASS、Galileo等联合解算会取得更好的精度。

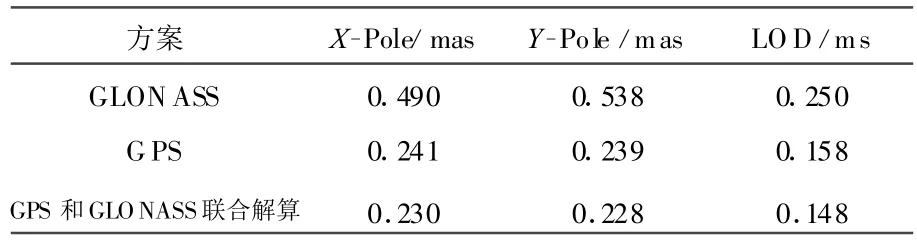
表1 不同方案解算的ERP系列与IERS Bulletin A系列的差值的均方根

4 结 论

利用优选的22个全球均匀分布的IGS跟踪站的GPS观测资料解算地球自转参数,得到了在IERS的ERP估计精度范围之内的良好结果。由分析可见,要独立解算精度较理想的地球自转参数必须构建更合理的全球连续监测与评估系统网。COMPASS全球连续监测与评估系统跟踪网的合理布局与利用COMPASS观测资料解算地球自转参数,是COMPASS全球连续监测与评估系统建设中的两个重要难题。此研究对于今后运用COMPASS资料解算地球自转参数以及全球连续监测与评估系统跟踪网的布局都有一定的参考价值。

[1]IERS.What is Earth Orientation Rapid Service/Prediction Center for Earth Orientation Parameters.[EB/OL].(2009-09-11),US Naval Observatory:http://maia.usno.navy.mil/whatiseop.html,

[2]Documentation for the GAM IT GPS Analysis Software[M].Massachusetts:Massachusetts Institute of Technology,2000.

[3]GAMITReference Manual[M].Massachusetts:Massachusetts Institute of Technology,2006.

[4]Xu G H,GPS:Theory,Algorithms and Applications[M].2th ed.Berlin:Springer,2007.

[5]周忠谟.GPS卫星测量原理与应用[M].北京:测绘出版社,1997.

[6]Zhu S Y,Mueller I I.Effects of adopting new precession,nutation and equinox corrections on the terrestrial reference frame[J].Journal of Geodesy,1983,57(1):29-42.

[7]Hugentobler U,Springer T,Schaer S,et al.CODE IGS Analysis Center Technical Report 1999[R].IGS 1999 Technical Reports,IGS Central Bureau,JPL,Pasadena,1999.

[8]Rothacher M,Weber R.Benefits from a Combined GPS/GLONASS Analysis for Earth Rotation Studies[C]//Proceedings of the ION GPS-99,Nashville,Tennessee,1999.