基于优化空间矢量脉宽调制算法的变频器中点平衡控制*

2010-08-28马文忠吴海波郭江艳

电机与控制应用 2010年6期

马文忠，吴海波，郭江艳

(中国石油大学(华东)，山东东营 257062)

0 引言

近年来，随着电力电子技术的发展，高压大功率多电平变频器得到了越来越广泛的应用，正日益成为研究的热点。其中，二极管中点嵌位型(Neutral Point Clamped，NPC)多电平变频器由于其成熟的拓扑结构和较好的应用效果，已成为多电平变频器中研究和应用最多的类型。但是，在NPC型多电平变频器的应用过程中，也出现了许多亟待解决的问题。其中，中点电位不平衡就是比较突出的问题之一。中点电位不平衡将带来输出电压波形畸变、电平数降低、逆变器开关器件承受的电压不均衡、电容的寿命降低等危害［1-8］。本文将以应用最为广泛的NPC三电平逆变器为研究对象，对其中点电位不平衡问题进行分析研究，并采用一种优化空间矢量脉宽调制(Space Vector Pulse Width Modulation，SVPWM)算法对中点电位进行控制，其算法也可以推广到任意多电平结构的逆变器中。

1 NPC型三电平逆变器中点电位不平衡的机理

二极管箝位式三电平逆变器的拓扑结构如图1(a)所示。对于三电平逆变器来说，每一相有P、O、N三个状态，所以共有33=27种电压状态组合，得到逆变器输出电压空间矢量的分布情况如图1(b)所示。

导致逆变器中点电位不平衡的主要原因如下。

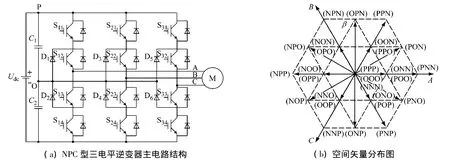
图1 三电平逆变器主电路结构及空间矢量分布图

(1)逆变器电路结构及控制策略对中点电位的影响。

三电平逆变器除零矢量外，共有24种开关状态，各种状态下交流负载的连接形式虽不尽相同，但其连接情况可归结为图2所示的五种连接方式。图2以四种不同矢量的五组开关状态PNN，OOO，PON，ONN和POO为例，画出了三电平逆变器电路拓扑和电流回路，分析不同开关状态时中点电流及电压的情况。

在三电平逆变器的19个基本矢量中，大矢量对应的开关状态使三相输出和正负母线相连，不影响中点电压;零矢量使负载三相短接，挂在正、负、零母线之一，也不会导致中点电压的变动。中矢量和小矢量的开关状态对应至少有一相输出和零母线相连，并与正、负母线形成电流回路，从而导致电容C1和C2充放电，使中点电压发生波动。

图2中inp为中点电流，流出中点为正。显然，大矢量和零矢量时开关状态的中点电流inp=0，电容C1和C2上的电压保持不变，处于平衡状态(不考虑充电电阻的影响)，如图2(a)、(b)所示。当中矢量开关状态为PON时，如图2(c)所示，有inp=ib，当负载电流ib＞0时，上电容C1充电，UC1升高，下电容C2放电，UC2下降，从而中点电位Umo=(UC1-UC2)/2下降;反之，ib＜0，则C1放电，C2充电，中点电位Umo上升。可以看出，电流方向不同时，对中点电压的影响也不同。对于小矢量的开关状态ONN，满足inp=ia，如图2(d)所示;而对开关状态POO，有inp=ib+ic=-ia，如图2(e)所示，显然ONN和POO两组开关状态对中点电压的作用完全相反。

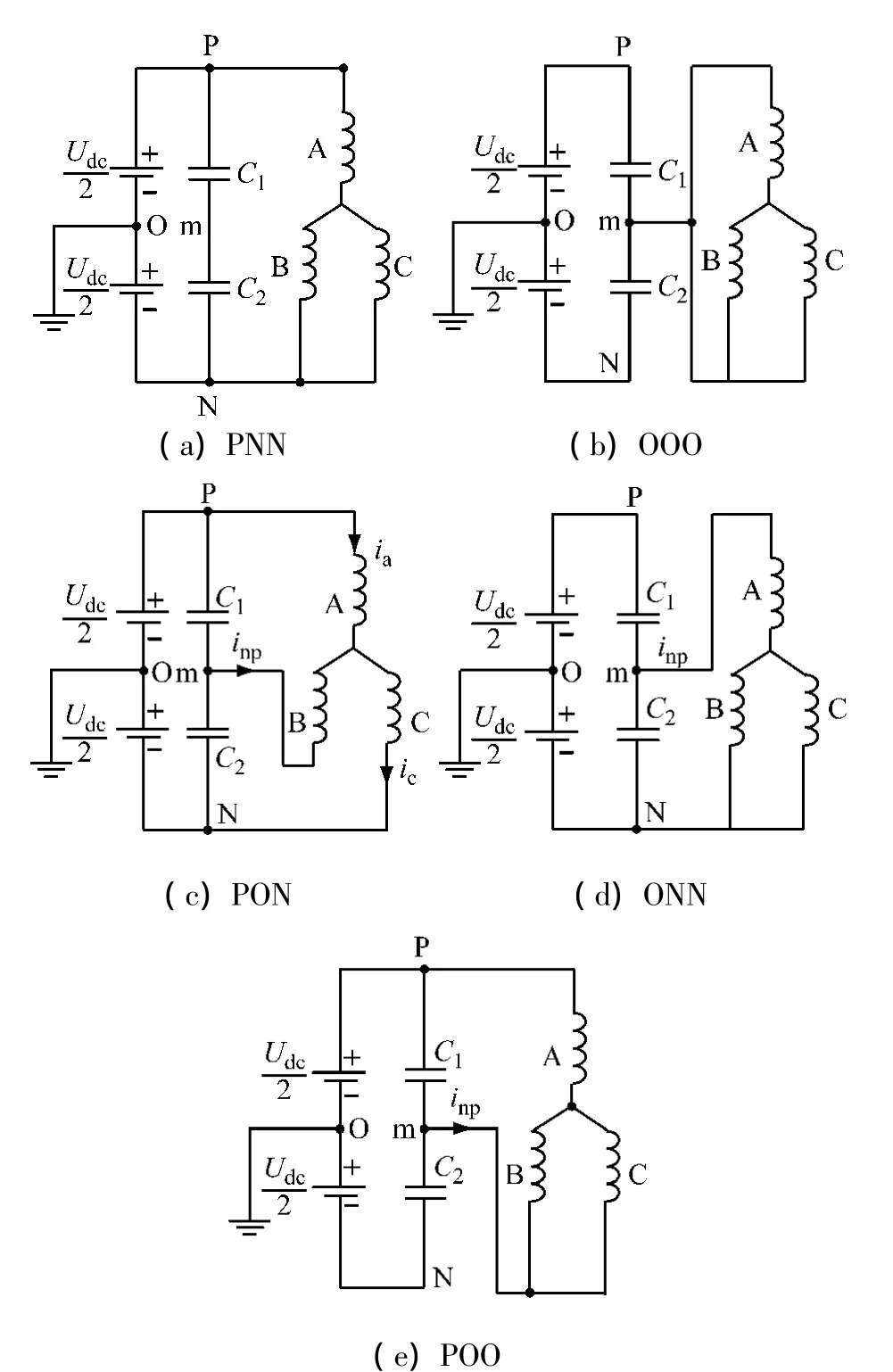
图2 基本矢量对应的实际拓扑和电流回路

(2)与直流母线电容有关。首先两个电容在制造工艺上不可能达到完全相同，势必会造成中点电压的固有偏移;其次，电容值的大小与直流侧电压平衡关系密切，电容值越小，电压波动必然越严重，所以电容值要尽可能大，但考虑到成本和制造工艺上的限制，电容值又不能取得过大。

(3)与负载有关。负载越重，中点电流越大，中点电位波动越大，造成的不平衡也越严重;负载功率因数也与中点电流的相位关系密切，是影响中点电压的重要因素。

(4)与输出相电压的幅值有关。幅值越大，小矢量参与成分越小，中点电压控制越困难。

(5)输出电压基波频率也决定中点电压的波动频率。

2 NPC三电平逆变器中点电位平衡控制

中点电位不平衡问题引起了学者的广泛关注，也已提出了很多解决方案，目前主要分为硬件控制策略和软件控制策略两种。一般硬件控制策略能够取得较好的控制效果，但将大幅增加电路成本，因此限制了其应用［8-15］。本文经过分析研究，通过优化SVPWM的控制算法，来实现中点电位平衡的控制。具体控制策略如下。

由以上中点电位不平衡的机理分析可知，零矢量和大矢量作用时，由于中点不参与能量的传送，因此它们对中点电位没有影响;而中矢量和小矢量作用时由于中点处都会有电流流过，也即有能量的流动，因此它们会带来中点电位的不平衡。其中每个小矢量都有两种开关状态(正小矢量和负小矢量)，而且这两种开关状态对中点电位的影响刚好相反。因此，合理安排正、负小矢量的作用时间，就可以很好地平衡中点电压。在三电平的空间矢量中，依据最近三矢量原则合成参考矢量时，至少会用到一个小矢量对。因此，该算法通过调整正负小矢量对的相对作用时间，对中点电压偏差进行补偿。

该算法首发矢量都采用正小矢量，满足同一桥臂不会从N状态直接到P状态切换，且开关状态切换时，三相桥臂中只有一相开关动作。在控制中点电位时只需检测该矢量作用时连接到中点的某相实际负载电流方向，即可知道该小矢量对直流电容电压的影响方向，并考虑到直流电容电压UC1和UC2的不平衡方向，进而调整正负小矢量的相对作用时间。

定义:ΔU=UC1-UC2。当 ΔU＞0时，表示电容C1上的电压偏大，则应该加大正小矢量的作用时间，以增加电容C1的放电时间，使之电压降低;反之，当ΔU＜0时，则应该减小正小矢量的作用时间。这里为了避免中点电位的小波动造成开关管频繁动作，导致出现开关损耗增加的情况，定义一个阈值h，即当ΔU＞h或ΔU＜-h时才进行调整。增大或减小小矢量的作用时间都通过乘以一个调制因数k来实现。考虑到实际应用中脉冲切换的死区时间，一般取0.25＜k＜0.75，具体控制规律如下:

当-h≤ΔU≤h时，k取0.5;

当ΔU＞h，且此时首发小矢量对应的中点电流的方向为流入，则k＞0.5，否则k＜0.5;

当ΔU＜-h，且此时首发小矢量对应的中点电流的方向为流入，则k＜0.5，否则k＞0.5。

得出调制因数后，将之与小矢量作用时间组合，优化小矢量的作用时间，就可以抑制ΔU，从而削弱中点电位的不平衡。以参考矢量位于第一扇区为例进行说明(由矢量分布的对称性，其他扇区的情况均可转化为第一扇区进行计算)，空间电压矢量示意图如图3所示。

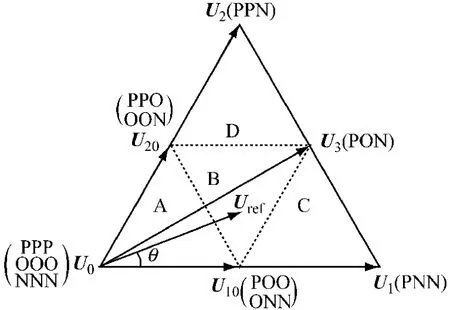
图3 第一扇区空间矢量分布示意图

T10、T20、T3为矢量 U10、U20、U3合成参考矢量Uref时分别对应的作用时间。考虑到调制因数k，得到优化后的一个周期Ts内各矢量的作用时间分配时序图，如图4所示。

按照上述算法重新进行空间电压矢量的合成，即可有效抑制中点电位的不平衡问题。

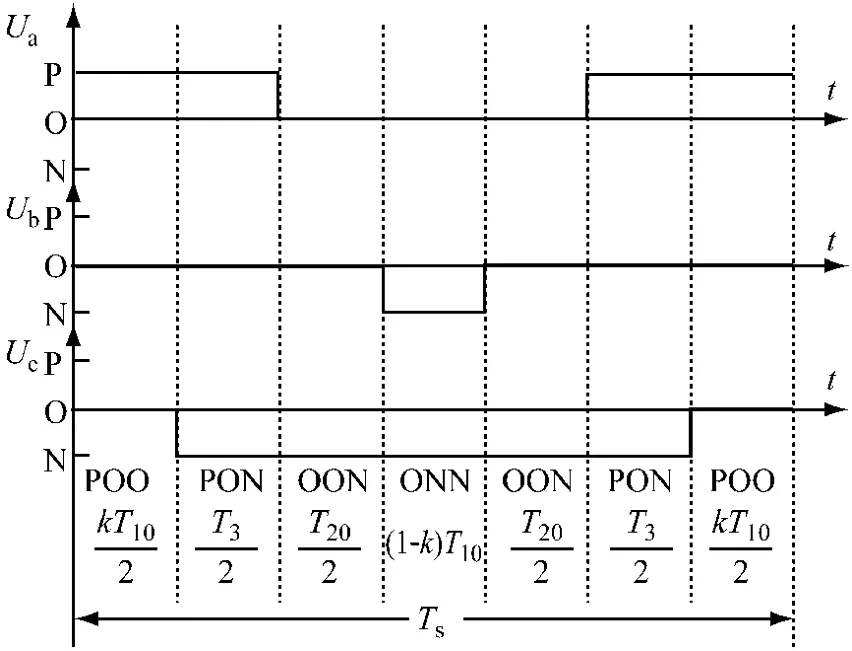
图4 一个周期Ts内加入调制因子k后电压矢量分配时序图

3 控制算法的MATLAB仿真分析

针对以上控制算法，采用MATLAB/Simulink搭建仿真模型，进行了仿真分析。仿真中直流侧电压为800 V，负载为阻感负载，功率因数取为0.886，开关管的频率为4 kHz。仿真得到中点电位波形如图5所示。

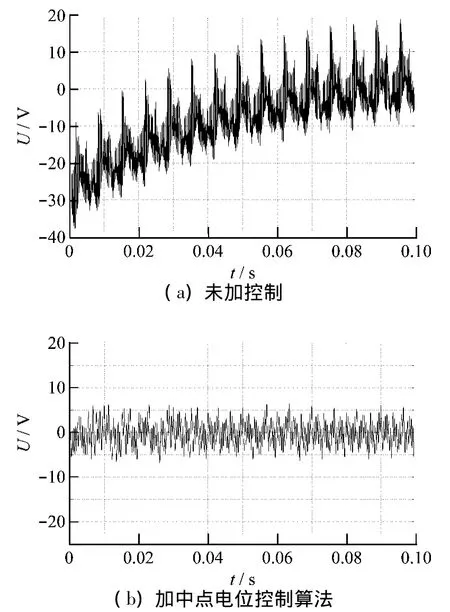
图5 仿真分析中点电位波形

由仿真结果可知，该软件控制方法可以有效抑制中点电位的偏移。

4 试验

在实验室搭建了一套NPC的三电平逆变器控制系统，并使用TMS3202812 DSP芯片对中点电位抑制算法进行了编程，实现了对逆变器系统的控制，得到试验波形如图6所示。

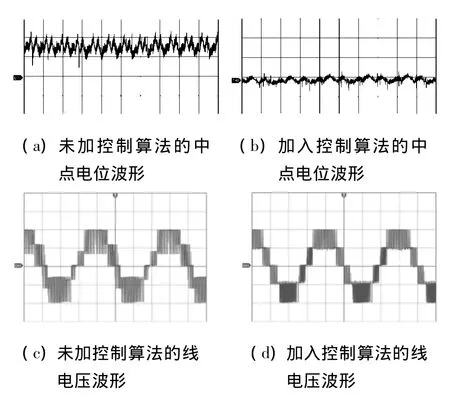
图6 试验波形

图6(a)是未加控制算法的中点电位波形，可见中点电位有较大偏移;图6(b)是加入控制算法的中点电位波形，可以发现中点电位不平衡得到了较好抑制。另外，图6(c)是未加控制算法的线电压波形，可以发现由于中点电位的偏移，输出线电压波形发生了畸变;图6(d)是加入控制算法的线电压波形，输出线电压波形比较理想，畸变得到了有效抑制。试验结果表明，使用本文所述中点电位平衡算法后，中点电位不平衡问题得到了有效解决。

5 结语

由于电路器件、拓扑结构、控制方法及负载工况等因素的影响，NPC多电平逆变器在应用过程中存在中点电位不平衡问题，并带来相应的许多危害。本文通过分析中点电位不平衡的产生机理，通过优化SVPWM控制算法，确定适当的调制因数，合理安排电压空间矢量中正、负小矢量的作用时间，可以较好地抑制中点电位的不平衡。理论分析、计算机仿真和试验研究，都验证了该控制算法的有效性。

［1］周文生，姚钢，宋文祥.中点箝位型三电平逆变器控制方法的综合研究［J］.电气传动自动化，2008，30(2):6-9.

［2］宋文祥，陈国呈，武慧，等.一种具有中点电位平衡功能的三电平空间矢量调制方法及其实现［J］.中国电机工程学报，2006，26(12):95-100.

［3］毛承雄，李时华，陆继明，等.中性点箝位型三电平高压变频器实验分析［J］.电力系统及其自动化学报，2008，20(2):78-82.

［4］罗永吉，尹华杰，周艳青.三电平NPC逆变器中点电位平衡的软件算法［J］.电气传动，2008，38(5):3-7.

［5］宋永祥，陈国呈，陈陈.基于矢量分区的三电平中点波动机理分析的研究［J］.电工电能新技术，2007，26(4):17-20.

［6］宋强，刘文华，严干贵，等.基于零序电压注入的三电平NPC逆变器中点电位平衡控制方法［J］.中国电机工程学报，2004，24(5):57-62.

［7］张卫丰，余岳辉，刘璐.三电平逆变器空间矢量控制算法仿真研究［J］.电力电子技术，2006，40(1):3-5.

［8］朱希容，周晓锋，周渊深.NPC三电平逆变器SVPWM算法的研究及仿真实现［J］.淮海工学院学报，2007，16(1):27-30.

［9］宋文祥，陈国呈，束满堂，等.中点箝位式三电平逆变器空间矢量调制及其中点控制研究［J］.中国电机工程学报，2006，26(5):105-109.

［10］桂红云，姚文熙，吕征宇.三电平变换器中点电压平衡问题的研究［J］.电源技术应用，2004，7(9):526-529.

［11］刘学超.三电平逆变器中点电压平衡的电压空间矢量控制原理及算法［J］.电源技术应用，2003，6(5):235-238.

［12］Nabae A.A new neutral-point-clamed PWM inverter［J］.IEEE Transactions on Industry Applications，1981，17(5):518-523.