基于系统动力学的大型设备的液压系统预防维修模型研究

谷高全，夏火松

GU Gao-quan ，XIA Huo-song

（武汉纺织大学 经济管理学院，武汉 430073）

0 引言

目前部分大型设备维修成本居高不下，成为企业沉重的经济负担，对企业的发展极为不利，影响企业的竞争力[1]。传统上，研究降低维修成本的研究方法主要运用成本管理理论、维修管理理论和系统工程理论[2]，而在大型设备的液压系统预防维修理论方面，典型的方法有：利用各维修因素的相关性，采用系统工程中的解释结构模型法对各影响因素进行分析[3]。虽然这方法取得了较好的效果，但它忽略了系统最主要的本质，同时各因素会随着外部的一些因素发生变化，所以必须利用动态、统一的观点来分析各个因素之间的相互联系和影响。

本文通过对大型设备的液压系统预防维修问题进行分析，确定研究边界和易于量化的特征变量，梳理大型液压系统在维修过程中各因素之间的关系，利用系统动力学理论构建模型和仿真，并对结果进行了分析，同时也对其中若干关键参数的影响规律进行了研究。

1 基于系统动力学的维修分析

系统动力学（System Dynamics，简称SD）是美国麻省理工学院（MIT）的Forrester教授在1956年建造的一种电脑模拟模型[4]。它以反馈控制理论为基础，以计算机仿真技术为手段，用定性与定量相结合的方法来以研究复杂系统问题。经过50多年的发展和完善，已经形成了完整的理论体系，并开发出了一系列建模仿真软件，如Anylogic、Vensim等。由于它在实现复杂系统建模和行为模拟方面具有优势，已被应用于多个学科[5]。

系统动力学的观点认为，系统应具有反馈、动态等特征[6]。反馈是控制系统的一种方法。它是把系统输出去的一部分信息（给定信息）作用于被控对象后产生的结果（真实信息）再返回给输入，并对系统的再输出产生影响的过程。SD认为几乎所有人工系统都是反馈系统 。动态系统所包含的量是随时间变化的，能以时间为坐标的图形表示[7]。譬如，人口的增长，就业人数的增减，城镇与农村的生活质量和物价的涨落等都是动态问题。

SD的基本思想是充分认识系统中的反馈和动态性，并按一定的规则逐步建立SD的结构模式。SD中的动态性，不是随机的不稳定的动态性，而是可以预期的，有一定规律的动态性。同时，某个变动经常在时间上表现出一定的延迟[8]。

用SD的观点来研究大型设备的液压系统预防维修问题，大致可以分为几个阶段：

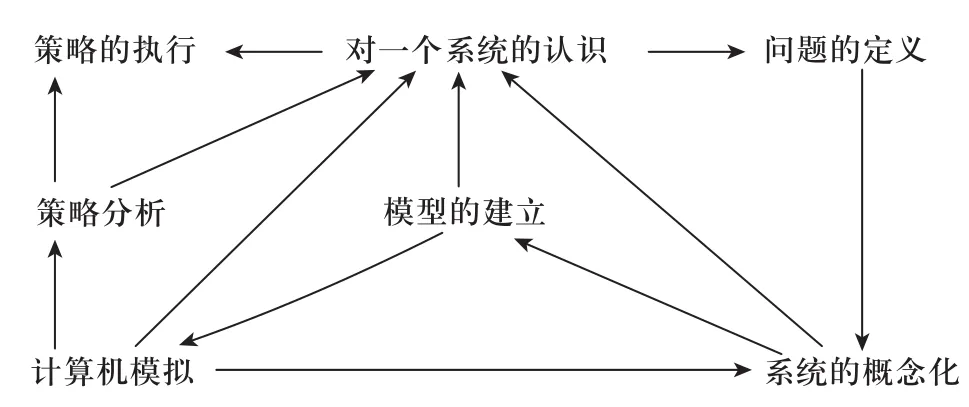
图1 系统动力学研究阶段

1）问题的定义：大型设备指单台（套）金额在170万元人民币（或20万美元）以上的设备[9]。对于大型设备的液压系统来说，它的预防维修相对于其他的系统来说更加的复杂，传统的维修模式已经不能适应当前维修的需要，所以需要采用新的维修模式。

2）系统的概念化：对大型设备的液压系统的结构进行分析，这一步的主要任务在于处理系统信息，分析系统的反馈机制；划分系统的层次与子块，定义变量，确定变量的种类及主要变量，分析系统的变量、变量间关系；确定回路间的反馈耦合关系，初步确定系统的主回路及它们的性质，分析主回路随时间转移的可能性。

3）模型格式化：确定大型设备的液压系统预防维修中的状态、速率、辅助变量和建立主要变量之间的数量关系；设计各非线性表函数和估计各类参数；给所有N方程、C方程与表函数赋值。

4）模型行为的分析与策略分析：以SD理论为指导进行模型模拟与政策分析，进而更深入地剖析大型设备的液压系统预防维修的问题；寻找解决问题的策略，并尽可能付诸实施，取得实践结果，获取丰富的信息，发现新的矛盾与问题。

每个阶段的起点和终点以及整个过程的起点和终点都是对这一系统及其问题的不断深入的理解。因此，它是一个环或者网，而不是线性的序列。一个循环之后又可以开始新的一个循环，可以不断反复迭代。

2 模型分析与构建

图2表示事前维修活动如何防止大型设备的液压系统故障的发生。X点表示缺陷发生，Y点表示故障发生，竖线表示事前维修活动。假如检查是完全的，即检查液压系统时，能检查出所有存在的缺陷。那么，事前维修找出了第2个和第4个缺陷，并防止这两个缺陷的进一步发展成为故障。

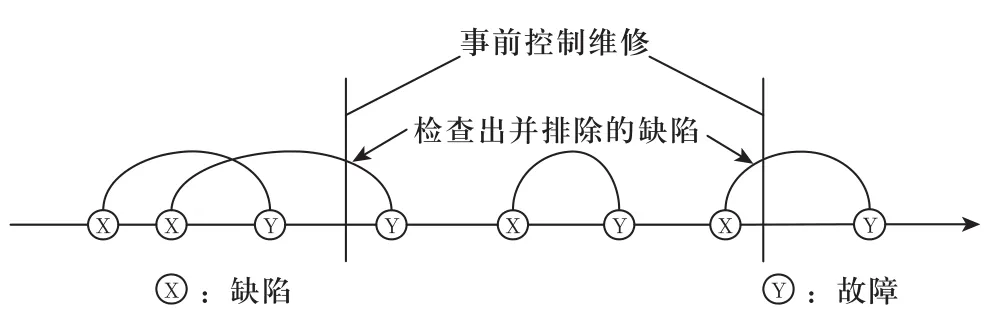
图2 事前维修如何预防故障的发生

从图2所知，液压系统不工作的主要原因有两类：一类是液压系统运行时出现故障；第二类是对液压系统进行检查（事前维修活动）而造成的系统停机。在这里，由于液压系统故障原因而造成的液压系统停机时间简称为故障时间，由于检查原因而造成的液压系统停机时间称为检查时间。如果检查间隔时间过长，虽然可以减少检查时间，但故障发的机会增多，故障时间将相应地增大；如果检查间隔时间较短，可以有效地防止故障发生，减少故障时间，但由于过频的检查使得检查时间大幅度增加。因此，建模目的就是在故障时间和检查时间之间寻找平衡点，确定出合理的维修间隔期，使得单位时间内总的停机时间期望值最小[10]。

大型设备的液压系统运行一段时间以后，液压系统的温度开始逐渐升高，而温度升高以后就容易导致缺陷增加，另外人员的操作失误也会使缺陷增加，缺陷累积到一定程度的时候，从而导致了故障的发生，因此这是一个正反馈。而液压系统故障的增加影响了维修效率的提高，维修效率的积累使大型设备的液压系统的维修度不断地增加，维修度增加到一定的时候液压系统的维修就已经完成了，已经修好的大型设备的液压系统经过一段时间以后，又开始不断地出现故障，因此这是一个负反馈，其系统因果关系如图3所示。

图3 液压系统维修的因果关系图

最后以重型机床（20-10FP500NC）为例子使用系统动力学软件Vensim构建其液压系统维修的SD模型如图4所示。

3 参数确定

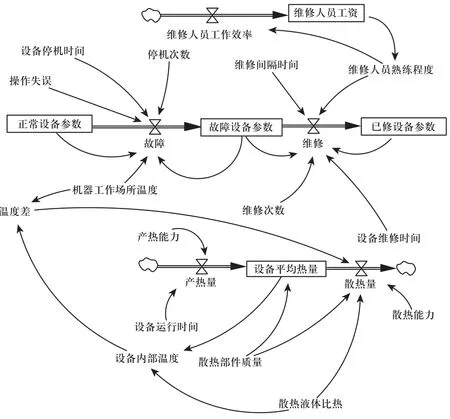
图4 液压系统维修的系统动力学模型

大型设备的液压系统在运行过程中，电能转换成其他形式的能源，同时也会产生大量的热量，这些热量由设备的散热系统排出[11]。目前先进的液压系统大都是用水冷散热器来散热，散热液体的比热也是模型中的变量之一。当外界的温度变化时，液压油的质量特性和液压元件的工作状态会发生相应的变化，加之液压元件的可靠性较差，因此大型设备需要在一定温度的工作环境中[12]。大型设备的液压系统维修工作是由工人来实施的，维修工作人员的工作效率也影响着液压系统从故障到修复的时间，本文用维修人员的工资来确定维修人员工作效率这个变量。大型设备的液压系统维修过程中的状态变量、速率及辅助变量集以及各变量的方程如表1所示。

表1 模型中涉及的变量

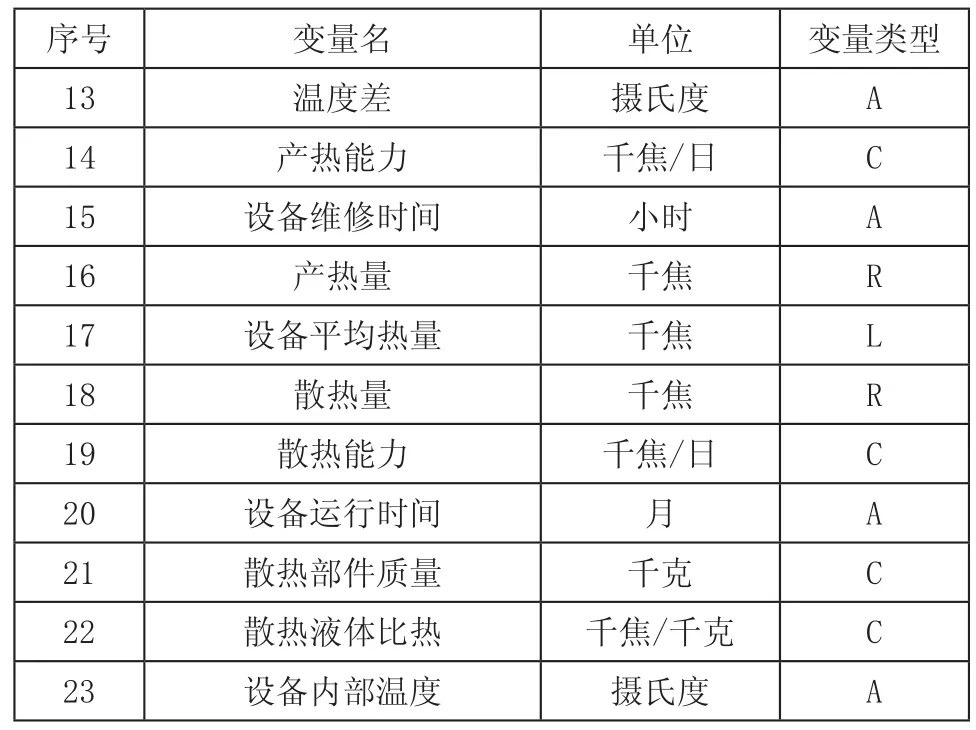
大型设备的液压系统维修过程不仅需要人力和技术的投入，时间的消耗也是不可缺少的。为了解决这一间题，引入系统动力学中的DELAY1函数。其函数形式为DELAY1（input，delay time），其中的延迟时间（delay time）即为维修间隔时间。其他辅助变量或常量的初始值，通过参考相关统计数据或根据经验设置。系统运行的时间单位为日，共运行20个周期，时间间隔为0.125个周期。在模型的运行过程中，除了对大型设备的液压系统过程的基本规律进行仿真之外，还考察了部分模型运行参数对仿真结果的影响。本文重点研究了故障率和维修效率改变时对大型设备的液压系统维修过程中的影响规律。具体参数如表2所示。

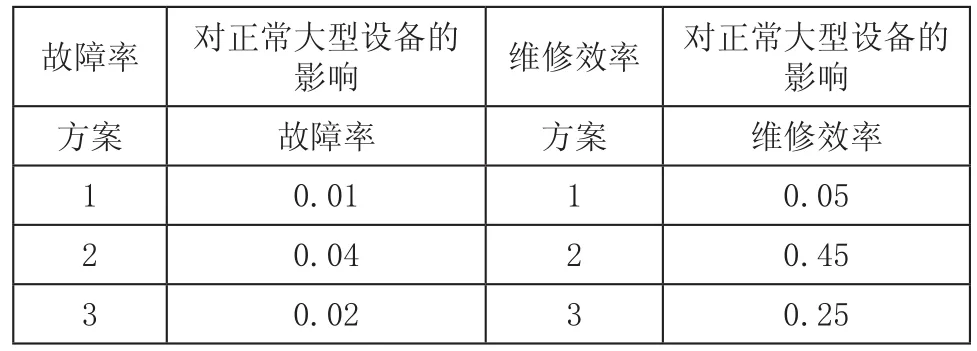
表2 模型运行参数的取值

4 结果与分析

模型的运行结果如图5所示，其中纵坐标为正常液压系统的参数。在大型设备的液压系统运行的初期由于对大型设备的液压系统使用缺乏经验和液压系统在安装调试的阶段时故障率比较高，但是设备运行了一段时间以后液压系统故障趋于稳定，不再出现故障率波动的现象，所以大型设备的液压系统参数为恒定的直线。

分别选择了故障率为0.01、0.04和0.02等不同的工作状态进行模型模拟可以看出当在不同的故障率和不同的维修效率下，最佳的维修间隔的天数是不同的。如图6所示。

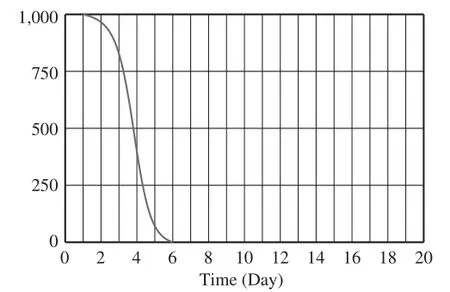
图5 模型运行结果

图6 不同参数下的运行结果

5 结论

利用系统动力学的观点对大型设备的液压系统预防维修系统的主要特征和基本演化规律进行了分析和探讨。通过分析认为，大型设备的液压系统预防维修系统是具有动态行为的高阶次非线性复杂系统，其边界具有多重反馈环，系统的各个组成部分之间，具有复杂的相互依赖关系。这些特点决定了大型设备的液压系统的预防维修适合用系统动力学的方法来研究。本文研究了故障率和维修效率等参数对大型设备的液压系统预防维修系统行为的影响规律，得到预防维修在不同参数下的间隔天数，模拟结果合理。系统动力学具有独特的方法学优势，为实现复杂系统的仿真和模拟提供了新的思路。

[1]杨桂霞,马忠臣.现代设备维修策略与维修技术综述[J].机械工程师,2008,(12).

[2] Tsai Y T, Wang K S, Tang H Y.Optimizing preventive maintenance for mechanical components using genetic algorithms[J].Reliability Engineering and System Safety,2001, 74：89-97.

[3]金玉兰,蒋祖华,侯文瑞.以可靠性为中心的多部件设备预防性维修策略的优化[J].上海交通大学学报,2006,(12).

[4]王其藩.系统动力学[M].北京：清华大学出版社,1994.

[5] Park D, Jung G M, Yum J K.Cost minimization for periodic maintenance policy of a system subject to slow degradation.Reliability Engineering and System Safety,2000, 68：105-112.

[6]王其藩.系统动力理论与方法的新进展[J].系统工程理论方法应用,1995,4(2)：6-12.

[7] Dhillon B S, Fahri Kirmizi.Probabilistic safety analysis of maintenance systems[J].Journal of Quality in Maintenance Engineering.2003, 9：303-320.

[8] Haritha Saranga.Opportunistic maintenance using genetic algorithms.Journal of Quality in Maintenance Engineering,2004, 10(1)：66-74.

[9] http：//zhidao.baidu.com/question/53789383.html

[10]方淑芬,吕文元.设备维修管理智能决策支持系统的研究[J].系统工程理论与实践,2001,(15).

[11] Francis K N Leung, Lai K K.A case study on maintenance of bus engines using the sequential method.International Journal of Quality＆Reliability Management, 2003,20：254-266.

[12] 李洪.液压控制系统[M].北京：国防工业出版社,1981：74-60.