基于概率神经网络的计算机网络安全仿真分析

王 伟

WANG Wei

（西安财经学院，西安 710061）

0 引言

随着计算机网络的迅速发展和广泛应用，网络安全问题变得越来越复杂，网络安全评价正成为网络技术发展关注的热点问题。网络安全评价的常见方法有模糊综合评判法、数据包络分析法、灰色聚类法等，由于这些方法建模和运算复杂，一些学者将BP神经网络引入到网络安全的评价中。这种基于梯度下降规则的算法存在收敛速度缓慢、容易陷入局部极小以及网络结构难以确定等缺陷，这些都大大影响了网络的学习效率和分类精度。针对BP算法的不足，本文将概率神经网络(Probabilistic Neural Network，PNN)模型应用于网络安全的分析中，采用Matlab工具软件对计算机网络安全指标的数据进行仿真训练和验证，然后将其与BP算法仿真分类的结果进行比较，分析表明：PNN网络设计时间极短，速度远快于BP算法；网络安全等级分类的准确率较BP网络明显提高。

1 基于PNN模型的网络安全分析

概率神经网络是D.F.Specht博士1989年提出的一种径向基函数(RBF)网络的重要变形[1]，这种基于统计原理的神经网络模型在分类功能上与最优贝叶斯(Bayes)分类器等价,具有训练时间短且不易收敛到局部最小点的优点，特别适合于求解模式识别问题。

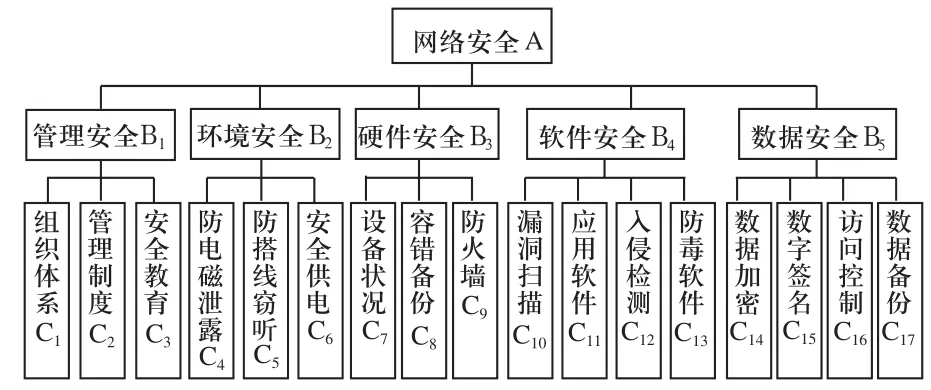
图1 计算机网络安全评价指标体系

1.1 网络安全评价指标体系

本文采用参考文献[2]的内容、准则和Delphi法筛选出上面图1中所示的评价指标，构成网络安全综合评价指标体系。网络安全综合评价指标共17项，每项指标由专家进行考评，并量化处理为[0,1]之间的数值，分值越高表明单个指标的安全程度越高。网络安全分为四个等级，即安全状态（1-0.85）、基本安全（0.85-0.7）、不安全（0.7-0.6）、很不安全（0.6-0）；其对应的类别表示为1、2、3、4。样本数据参见文献[3]，将16组样本数据对应的输出结果进行类别标示依次记为：1 2 2 4 1 2 3 4 1 2 3 4 1 2 3 4。

1.2 概率神经网络模型的建立和仿真

首先确定PNN网络的结构，根据径向基函数的特点，其输入层神经元个数与输入样本向量个数相同，输出层神经元个数等于训练样本数据的种类个数，每个神经元分别对应于一个数据类别。现分别用(1 0 0 0)、(0 l O 0)、(O 0 1 0)、(O 0 0 1)表示网络安全的4个等级1、2、3、4。PNN的结构为：输入层有17个神经元，输出层有4个神经元，中间层神经元的传递函数为高斯函数，输出层的传递函数为线性函数。

本文采用Matlab编写仿真程序，网络训练采用交叉验证的方法。令P表示网络的输入样本向量，T表示网络的目标向量，PNN网络的仿真步骤为：第一步，将表1中前9组数据用于训练，余下7组数据用于测试；第二步，用第一次作测试的数据（7组）来训练，而第一次用于训练的9组数据来测试。这样就相当于所有数据都用于测试了一遍，通过交叉验证得到属于每一类的概率，最后给出类别[4]。以下是用matlab6.5所编写的程序代码： t1 ＝ clock； P ＝ P’； T ＝ T’；

net＝newpnn (P, T, SPREAD)；%SPREAD取0.1

t2＝clock；timespan=etime (t2, t1)；%计算设计网络的时间； y_test＝sim (net, P_test);

yc_test＝ vec2ind (yc_test)；yc_test。

PNN第1步仿真结果为：timespan＝0.14s，yc_test＝2 3 4 1 2 3 4；PNN第2步仿真结果为：timespan＝0.157s，yc_test＝1 2 3 4 1 2 3 4 1。

1.3 BP神经网络模型的建立和仿真[5]

首先确定BP网络的结构，输出状态同PNN仿真的设置。根据Kolmogorov定理，选用一个N* (2N+1)*M的3层BP网络作为状态分类器；其中，N（N=17）表示输入特征向量的分量数，M(M=4)表示输出状态类别总数。BP仿真采用同前述PNN同样的方法和数据进行，第1步测试后7组数据的仿真结果为：timespan=16.828s,Y对应的仿真结果矩阵值为：

0.0131 －0.0076－0.0004－0.7659－0.0371－0.0200－0.0001

0.5890 －0.0742－0.0400－0.1017－0.6050－0.0361－0.0203

0.0503 －0.2819－0.0139－0.0048－0.1194－0.7303－0.0421

0.0071 －0.0220－0.9484－0.0010－0.0033－0.0130－0.9745

按照向量与等级类别的对应关系，可知仿真分类结果为：Y＝2 3 4 1 2 3 4 ；同理，第2步测试前9组数据的仿真结果为：timespan＝37.156s；Y＝ 1 1 3 4 1 2 3 4 1。

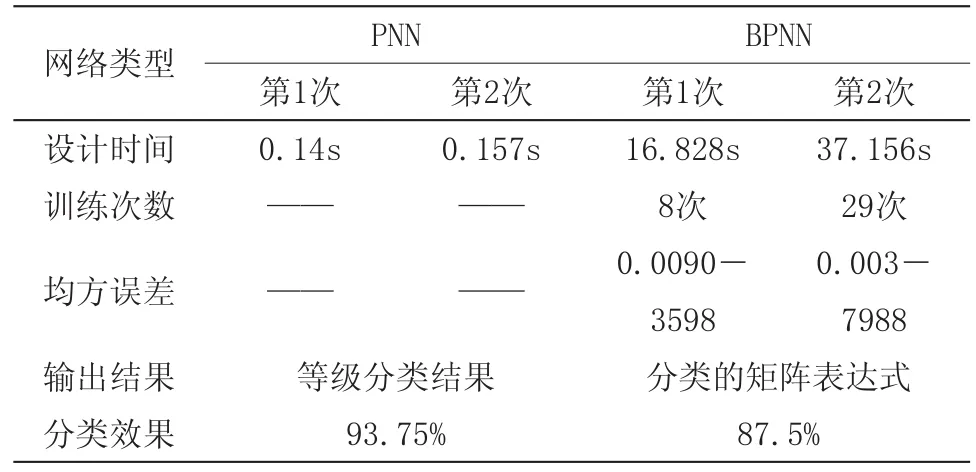
表2 计算机网络安全仿真分类情况对比

表2的数据对比说明：1）基于PNN的网络设计速度远远快于BP网络；2）PNN仿真的均方误差为0且分类的准确率较BP要高；3）PNN所得输出结果更直接明了。总之，运用PNN比BPNN对计算机网络安全仿真评价更优越。

2 结论

本文仿真研究表明：运用PNN模型对计算机网络安全等级进行评价，与BPNN模型相比：其训练速度快，不存在陷入局部极小点的问题，网络仿真输出的分类精度高，泛化能力强，特别适合于求解模式识别问题。本文的创新点在于：PNN模型的方法为全面有效的评价网络安全问题提供了新的思路和方法。

[1] 李冬辉,刘浩.基于概率神经网络的故障诊断方法及应用[J].系统工程与电子技, 2004, 26(7)：997-998.

[2] ISOPIEC17799-1：2005(E).The International Organization for Standardization.Information Technology-Security Techniques-Code of Pract-ice for Information Security Management[S].

[3] 许福永,申健,李剑英.基于AHP和ANN的网络安全综合评价方法研究[J].计算机工程与应用, 2005, 29：127-128.

[4] 周开利,康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京：清华大学出版社, 2005.

[5] 王宇浩,王海波.改进的BP神经网络在局域网故障诊断中的应用[J].计算机仿真, 2010, 27(4)：96-98.