配料计算的迭代解法及误差分析

□□严济军，杨伟东

配料计算的迭代解法及误差分析

Iterative Solution and Error Analysis on Mix Calculation

□□严济军1，杨伟东2

1 配料计算的实质

生料配料计算的目的是根据获得的各种原材料成分，寻找适当的配比，满足熟料质量和煅烧工艺的要求，并且使生产成本尽量降低。熟料质量和工艺要求通过率值控制来实现，率值变化范围决定硅酸盐水泥熟料成分中主要氧化物含量的波动范围。

无论是设计阶段还是实际生产过程中，首先要根据产品的质量要求结合生产设备以及原材料的情况确定目标熟料的率值。对于一条水泥生产线来说，熟料烧成系统的热耗作为重要的经济技术指标是基本固定的，选定燃料，熟料中的煤灰掺入量就基本确定。

给定目标熟料的率值和热耗，所用原煤的发热量和灰分，以及原料和煤灰的成分分析，可以计算出目标熟料的主要氧化物含量，去掉掺入的煤灰后就得到灼烧生料的主要氧化物含量，考虑烧失量容易换算成所需生料成分的目标值。以生料中各原料组成占比为未知数，可以得到一组线性方程，配料计算的实质就转化为求解线性方程组的问题。

2 求线性方程组数值解的迭代解法

硅酸盐水泥生产所用原料主要有石灰质原料，是熟料中CaO的主要来源；其次是粘土质原料，是熟料中SiO2等酸性氧化物的主要提供者；通常需要一些校正原料提供Al2O3、Fe2O3，或补充SiO2的不足。

由于影响率值的主要氧化物只有硅铝铁钙4种，所以无论是使用几种原料，均得到4个方程式组成的非齐次线性方程组。设满足要求的生料中硅铝铁钙4种氧化物的含量为S0、A0、F0、C0，当采用n种原料配料时，设每种原料中的硅铝铁钙的氧化物含量分别为Sj、Aj、Fj、Cj（j＝1，2，……，n），n种原料的配比设为xj（j＝1，2，……，n）。为了叙述的方便，我们不妨称之为钙方程、硅方程、铝方程和铁方程，即：

对于上述非齐次线性方程组，除了传统的高斯消去法，还可以运用数值分析中迭代的方法求解。从线性方程组的每个方程式中均可以分离出一个未知数，用其他未知数来表示。给定一组初始值，通过若干次迭代计算，可以求得线性方程组的解。

以4组分为例，方程组的解可以表示为雅可比（Jacobi）迭代：

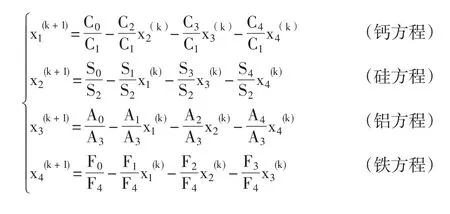
或高斯－塞德尔（Gauss－Seidel）迭代：

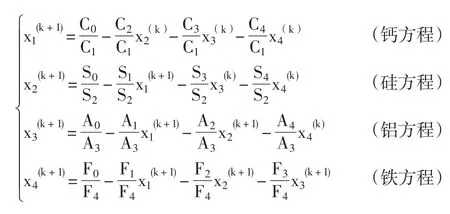
迭代的过程很方便在计算机上实现，无论是编制配料计算软件还是质量控制软件，均可使用该算法。事实上，在EXCEL试算表中即可简单实现，具体步骤从略。

3 迭代收敛的对角占优条件

并非随意建立的迭代都能够保证收敛。上述方程的次序是符合迭代收敛的条件的，即原始方程组的系数矩阵满足对角占优的条件。所谓对角占优即方程组对角线上的未知数系数的绝对值大于同行上其他未知数系数的绝对值之和。对角占优条件只是迭代收敛的充分条件，有时稍弱的对角优势甚至个别方程不满足对角占优，迭代依然能够收敛。

一般而言，石灰质原料中的CaO含量相比其他氧化物的含量要高，即石灰石的CaO含量占优。把石灰石作为组分1，石灰石中的CaO含量就是C1；同理，粘土质原料中SiO2的含量占优，铝质校正原料中Al2O3含量占优，而铁质校正原料中Fe2O3含量占优。将含量占优的组分安排在方程组对角线的位置，即粘土质原料作为组分2，SiO2含量作为S2，铝质校正原料作为组分3，其Al2O3含量作为A3，而铁质校正原料作为组分4，其Fe2O3含量作为F4，这样才能保证建立的迭代收敛。

三组分配料时，一般是粘土质原料中含铝或铁较高，即铝或铁与硅的含量相关。此时可以根据情况忽略铝方程或铁方程，以另外三个方程建立的迭代求解三个未知数，这样求得的解至少满足2个率值要求。

四组分配料时，如果每种组分中占优的氧化物都不同，那么直接根据对角占优的原则建立迭代即可。否则，要根据氧化物含量做适当调整。比如，使用高硅粘土作为硅质校正原料时，选择铝方程建立的迭代求粘土质原料比较适宜。

五组分配料时，同样根据对角占优原则建立迭代。可以将某两个组分按比例相加得到一个新的混合组分，按四组分的解法求出结果，再按比例分配即可。

4 精度控制和误差分析

迭代的精度控制可以设定，当前后两次计算结果的相对误差小于设定值时结束迭代计算。通常需要的精度受配料计量设备的精度限制，还与原燃材料的种类，预均化的效果，分析结果的准确性有关。

上述线性方程组解的误差，主要来源于两个方面。一方面方程组的系数是各原料化学分析值，分析结果的误差会引入到方程组的解中；另一方面，方程组的常数项是估算的目标生料相应氧化物的值，估算时，熟料主要氧化物的和值是经验值或按假定的原料配比估算而来，烧失量也是按假定的配比估算得来。估算的误差同样会引入到方程组的解中。

为了分析求解线性方程组过程中的误差，规定了矩阵的范数和条件数，用来刻画矩阵的接近程度以及方程组病态的程度。

方程组的系数矩阵为A，A的逆矩阵为A－1，相应矩阵的范数为‖A‖和‖A-1‖。矩阵的条件数cond(A)=‖A-1‖∙‖A‖。

系数矩阵的扰动对解的影响可用下式表示：

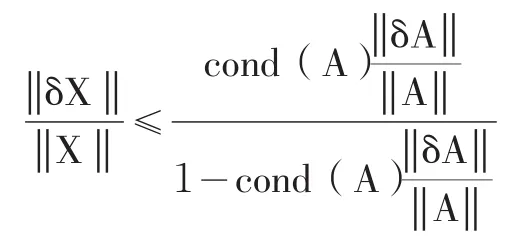
常数项的扰动对解的影响也可以表示为：

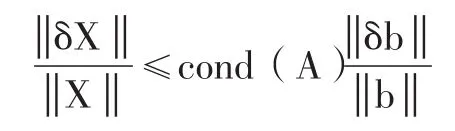
可见，系数矩阵的扰动和常数项的扰动对解的影响与条件数cond(A)的大小有关，条件数越大，扰动对解的影响可能越大，条件数的值刻画了方程组病态的程度。根据范数的性质：

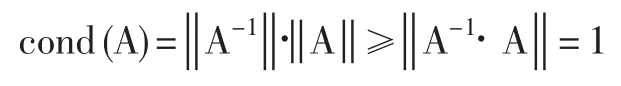
所以当条件数接近1的时候，方程组的性态是好的；反之，条件数越大，方程组的病态程度越高。可以认为，方程组的病态程度影响解的精确程度。笔者计算了一些4组分原料组的条件数，发现使用硅质校正原料时，条件数为15～17左右，使用铝质校正原料时条件数约为8～10，条件数随每种原料中占优的氧化物含量的优势程度而减小。

系数矩阵中原料成分分析结果相对误差1%时，如果条件数8，则解的误差会有8.7%；同样地，1%的常数项相对误差也会带来8%的误差。这就是说原燃材料很小的波动可能引起出磨生料很大的波动，因而，提高分析准确性和原燃材料的均化效果对于配料计算和生产质量控制非常重要。

[1]张池平.计算方法[M].北京：科学出版社，2006.

[2]沈威，黄文熙，闵盘容.水泥工艺学[M].武汉：武汉工业大学出版社，2002.

[3]李明豫，丁卫东.水泥企业化验室工作手册[M].徐州：中国矿业大学出版社，2002.

4刘笃新.水泥生料配料的率值公式法[M].北京：中国建材工业出版社，1992.

book=93,ebook=41

TQ172.614.1

A

1001－6171（2010）05－0093－02

通讯地址：1天津水泥工业设计研究院有限公司，天津 300400；2黑龙江三岭水泥有限公司，黑龙江 三岭 150323；

2010－01－11；编辑：吕 光