地铁车站地下连续墙泥浆槽壁的稳定性分析

2010-08-20徐永浩

山西建筑 2010年5期

徐永浩

0 引言

目前,全国很多大城市都有多条同时开工建设的轨道交通线路。地铁车站基坑一般开挖较深,为了减小基坑开挖对周围环境的影响,基坑的围护结构一般选用具有墙体刚度大、整体性强、可逆作法施工等优点的地下连续墙。然而地连墙有它自身的缺点和尚待完善的方面,其中槽壁坍塌问题是一个必须引起重视的问题。造成槽壁坍塌的原因很多:地下水位急剧上升、护壁泥浆液面急剧下降、含有软弱疏松或砂性夹层、泥浆的性质不当或者已经变质等。槽壁坍塌轻则引起墙体混凝土超方和结构尺寸超过允许的界限,重则引起相邻地面沉降、坍塌,危害邻近建筑和地下管线的安全[1]。因此对地连墙槽壁稳定性进行分析具有重要的研究意义。由于槽壁稳定的机理十分复杂,至今仍无明确定论,三维分析法更能反映槽壁失稳的真实破坏情况,因而得到了广泛的重视和应用。目前分析泥浆槽壁稳定的三维分析方法较多,常用的破坏体模型[2]有抛物线柱体、半圆柱体、楔形体等模型。由于不同模型的假设条件不同,得到的结果也不同。

1 影响槽壁稳定的因素

地下连续墙槽壁稳定性受到土层地质特性、护壁泥浆性能以及泥浆液面超高等多种因素综合影响[3,4]。

1.1 土层地质条件

毫无疑问,地基土的抗剪强度指标是影响开挖稳定性的主要因素之一。此外,土的密实度对稳定也有影响。不同土层条件下成槽过程中的稳定性特征不同,如地下水位、土体的渗透性等,均对槽壁稳定有相当影响,特别是地下水位高低影响更为突出。地下水位高低的影响主要在于地下水与槽内水之间的压差,压差是泥皮形成和高分子渗入胶结深度的主要因素,泥皮形成和高分子渗入胶结所形成的胶结作用又是槽壁稳定的重要因素。因此,地下水位的高低直接关系着槽壁的稳定,压差小,则泥皮不容易形成,高分子也不容易渗入到土体内,形成的胶结作用很弱,不利于槽壁的稳定。

1.2 护壁泥浆性能

泥浆具有一定的重度,将会对槽壁产生静水压力,可有效抵抗槽壁上水平土压力和水压力,形成槽段内的液体支撑,从而防止槽壁坍塌和剥落。泥浆重度与槽壁稳定呈正趋势关系,泥浆重度越大,护壁作用越强,槽壁就越稳定。

1.3 泥浆液面超高

如果泥浆重度过高,将会影响泥浆的泵送循环和泥土分离。因此,在泥浆重度达到优化值而不能继续提高以增大槽壁稳定性时,可通过泥浆液面超高来实现护壁泥浆的高内撑压力。

1.4 施工单元槽段的划分

单元槽段的长度决定基槽的长深比,而长深比的大小影响土拱作用的发挥,而土拱作用影响土压力的大小,一般长深比越大,土拱作用越小,槽壁越不稳定。

2 泥浆槽壁稳定性分析

2.1 基本假设

1)土体为各向同性的均质体;2)滑裂体为刚性体且不考虑内部变形;3)滑动面为倾斜的平面。

2.2 模型建立

假设槽壁的破坏体为一具有倾斜滑动面的半椭圆形,滑动面与水平面成α角,椭圆形的开口朝向泥浆槽,开口宽度等于泥浆槽段长度为 l,抛物线顶点到泥浆槽壁的距离为b,槽深为 h,见图1。

滑动面在XOY面的投影方程为:

以下是半椭圆柱体模型的几何参数的求解步序。

1)地下水位以上破坏体体积为:

2)滑动面DC下的体积:

3)地下水位以下的破坏体体积为:

4)滑裂体侧面积:为了计算简便,滑裂体的侧面积取相应的三棱柱的侧面积,如图3所示。

5)滑裂体底面积:

其中,b为破坏体厚度,m;h为破坏体高度,m;l为泥浆槽段长度,m;hw为地下水位到破坏体底部的高度,m;α为滑动面与水平面的夹角,(°)。

2.3 受力分析

破坏体所受的力包括:自重 W,破坏体范围内的地面荷载P,侧面粘聚力C侧,滑动面上的抗剪力Ps以及滑动面法向反力N等。各力的示意见图3。

1)破坏体自重 W。地下水位以上的土虽然处于毛细状态,但是仍按照天然重度算。地下水位以下土的重度取有效重度。

其中,γ为地基土的重度,kN/m3;γw为地下水的重度,kN/m3。

2)滑裂体的侧向粘聚力 C侧。

3)护壁泥浆压力Pf。泥浆具有一定的重度,泥浆在槽内将对槽壁产生一定的静水压力,可抵抗作用在槽壁上的侧土压力和水压力,相当于一种液体支撑,可防止槽壁坍塌和剥落。泥浆的护壁作用首先表现为泥浆的静水压力作用,但泥浆是具有触变性的特殊流体材料,对维持槽壁稳定起到维持静态液压的作用[5]。根据Bishop推出的结果,对于深槽泥浆护壁泥浆压力为:

其中,hf为泥浆液面到破坏体底部的高度,m。

4)地下水压力 Pw。采用传统的“水土分算”方法,将地下水单独抽出来作为外荷载施加于滑裂体上,由于挖槽施工过程较短,所以不考虑渗流力作用。

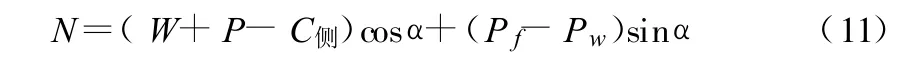
5)滑动面法向反力N。由滑动面法线方向力的平衡方程可得:6)滑动面抗剪力 Ps。滑动面的抗剪力为滑动面摩擦力与粘聚力之和,即:

其中,γf为泥浆重度,kN/m3;c为土体单位面积粘聚力,kN/m2;cf为泥浆单位面积粘聚力,kN/m2。

2.4 槽壁稳定安全系数

槽壁稳定性的安全系数可以表示为[7]:

其中,Fs为槽壁的整体稳定安全系数;Ff为滑动面土的抗剪力;F为平衡滑动体需要的滑动边界上的剪力。根据以上推导可得滑动面土体的抗剪力:

滑动体的下滑力:

将式(14),式(15)代入式(13),可得槽壁稳定性的安全系数:

2.5 泥浆最小重度

取Fs=1,将各力的表达式代入式(16)得到泥浆最小重度:

2.6 算例分析

取文献[2]的算例:地下墙深度37.5 m,地基土平均重度 γ=18 kN/m3,粘聚力 c=10.7 kPa,内摩擦角 φ=23°,地下水标高 hw=3.19 m,地面超载q=40 kN/m2。计算中固定开挖槽段的长度为6 m及滑动体的高度为地连墙深度37.5 m。将已知值代入式(17),得到当破坏体厚度 b=4.2 m,滑动面倾角 α=58.3°时,最小泥浆重度γf=8.832。