基于SUSAN分层快速角点检测的改进算法
2010-08-18马海超
赵 杰,马海超
(河北大学 电子信息工程学院,河北 保定 071000)
角点是图像的重要特征,它在保留图像重要信息的同时可有效减少数据量,而且对透视变换及变形都具有较强的鲁棒性[1]。利用角点特征可显著提高立体视觉匹配和三维重建算法的效率,因此,角点检测在图像匹配以及三维重建中具有重要意义。
角点检测算法主要分为基于图像边缘法[2]和基于图像灰度法[3]两大类。基于图像边缘法对边缘提取算法的依赖性较大,计算复杂且不能很好地定位角点。基于图像灰度的方法则不存在上述缺点,该方法又分为两类:一类是基于图像导数的Plessey[4]算法,其可靠性高,但计算复杂,速度慢;而另一类是基于图像灰度对比关系算法,如SUSAN算法,此类算法定位准确,具有积分特性,无需求导运算。因此,该算法在抗噪能力上具有较大优势,运算速度有所提高,但仍不能满足实时性要求。
基于上述分析,这里引入基于SUSAN算法的分层快速角点检测法与角点“性能好坏”判别算法相结合的角点检测法。采用由粗到细的分层策略,通过小波变换对角点进行粗略定位,再经“好坏”判别减少角点数量,最后运用SUSAN算法对角点进行精细查找,准确定位角点,从而有效解决了基于SUSAN算法的分层快速角点检测法在对实际图像进行角点检测时,角点数量太多,不利于角点匹配,计算速度慢的问题。
1 基于SUSAN的分层快速角点检测算法
基于SUSAN的分层快速角点检测算法是针对SUSAN算法在角点检测中运算速度较慢的问题而提出的。该算法根据图像中像素周围图像灰度的相似性和角点的特性,引入提升小波变换理论,采用由粗到细的分层策略,从而提高了运算速度。
1.1 提升小波变换理论
传统的小波变换受到Fourie变换的局限,而不依赖于Fourie变换的小波提升技术[5]实现了定位运算,可节省存储空间,提高运算速度。图1为提升小波变换原理框图。
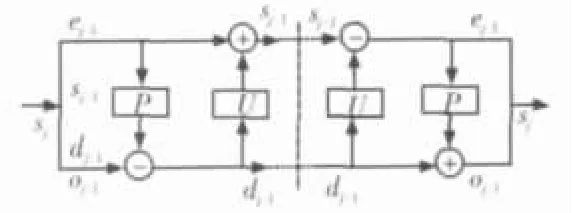
图1 提升小波变换原理框图
提升小波变换过程主要包括分裂、预测和更新3个步骤。其中,分裂是将原始信号分为两个互不相交的子集,最简单的分裂方法是将信号分为偶数序列和奇数序列,即

式中,S 表示分解操作;s,d 表示信号;j表示层数;e,o分别表示偶数序列和奇数序列。
预测是根据原始数据的相关性,采用偶数序列的预测值P(s)预测奇数序列的值,用来表示两者逼近程度,即

更新是保证变换后的图像保持原始图像的属性,用U产生一个更好的数值保留原始图像的一些特性,即

1.2 由粗到细的分层快速角点检测算法
直接运用SUSAN算法检测角点,速度较慢。而若能快速找到角点的粗略位置,再进行准确判断,则可大大节约时间。
小波变换后,原始图像分为低频区域和高频区域。低频区域是原始图像的近似表示,高频区域是原始图像的细节表示,能够描述细节变化。在图像中,大部分像素周围的灰度值相似,但角点附近像素的灰度值变化较大,且能反映小波变换的高频区域。小波变换的这种特性以及提升小波变换的高速算法为快速找到角点的大概位置提供条件。
分层检测法先对输入的图像进行提升小波行变换,再进行提升小波列变换,在其高频区域很容易检测到角点的粗略位置,最后用SUSAN算法精确定位角点。使用由粗到细的分层策略可大大减少运算时间。
快速、高效地粗略定位角点位置的关键在于快速、有效的提升小波变换。行、列图像的提升小波变换相似,这里以行图像为例说明。图2表示一行中两种典型图像。图中黑、白色圆圈表示像素的灰度,分别代表目标和背景。奇、偶表示目标从奇数或偶数位置开始。将原始图像按奇、偶分开,分裂后的结果如图3所示。

图2 一行中两种典型图像
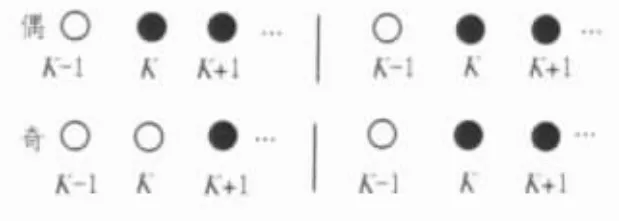
图3 图像的奇偶分裂结果
最简单的方法是小波预测法,有Harr小波预测和线性小波变换预测2种方案。如果采用Harr小波预测,即

预测后,从奇数位置开始的行由细节图像可以准确定位原来的起始位置(2k+1),但从偶数位置开始的行,由于其细节图像无法提供细节,不能准确判定角点的位置,如图4所示。

图4 图像的Harr小波预测
结合实时性要求及检测效果,采用线性小波变换的预测方法最好。即采用

线性小波预测可大大减少数据量,适合搜索角点的粗略位置。如图5所示,目标从奇数位置开始的行,根据其细节图像,计算出的起始位置为2k,可准确定位原来的起始位置。目标从偶数位置开始的行,计算出的起始位置为(2k-1),只出现1个偏移,为精确定位角点创造条件。
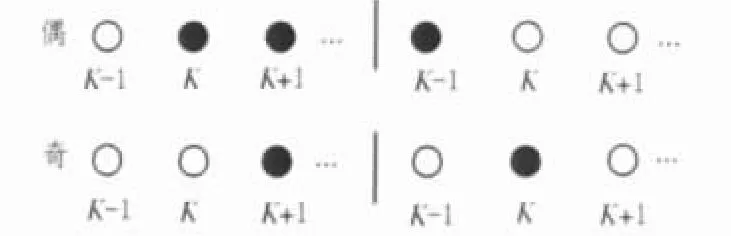
图5 图像的线性小波预测
2 角点“好坏”判定函数的引入
SUSAN分层快速角点检测法在检测角点时只能判断是否为角点,不能判断角点的“好坏”程度,这样在检测实际图像角点时应用效果不佳。通常一幅实际图像的特征点很多,若全部检测出来,会增加后续匹配的计算量。而如果随意去除部分角点,则会使图像缺失部分重要角点。虽然通过调整每幅图像阈值能够拼凑合适的角点数量,但计算量太大。基于此,这里在快速角点检测算法中引入评价角点好坏的判定函数。图6为USAN的6种典型情况。
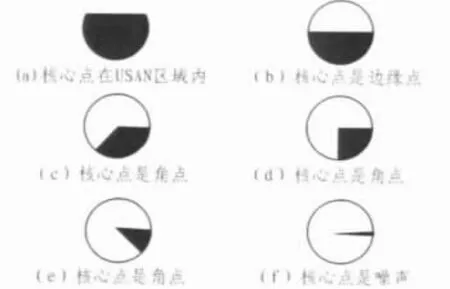
图6 USAN的6种典型情况
图6 中,角点有“L 型”、“T”型、“Y”型,“L 型”角点为好的角点。 图 6(d)为“L 型”角点,是 nmax的 1/4,这里定义为 ngood。图 6(b)则是一个边缘,图 6(f)可能是角点,也可能是噪声,但在实际图像中噪声的概率更大一些。图 6(c)和图 6(e)是普通角点。采用判定角点“好坏”的函数

式中,Y(r0)分布在(0,1)区间内。
对图像进行角点检测后,根据Y(r0)的大小对所有角点进行排序,选取最好的即可。但完全根据Y(r0)的大小排序后角点的分布不均匀,也不利于实现匹配算法。因此通过计算角点间的距离实现角点的均匀分布。距离计算公式如下:

式中,r0i、r0j分别是角点在图像上的坐标位置,ri是最小距离,Crobuse取值 0.9。
根据距离r对角点排序,这样可使角点均匀地分布在图像上,有利于图像的匹配。引入好坏判断函数后的算法具体步骤为:1)应用SUSAN算法计算图像上的所有角点;2)用式(6)计算角点好坏程度;3)由式(7)计算角点的距离;4)对距离排序,如果角点数量小于阈值(如取500)就取所有角点,如果大于阈值则取前500个角点。
3 试验结果
为验证本文算法的有效性,通过Microsoft Visual C++6.0进行一系列实验,如图 7所示。图 7(a)为原始图像,图 7(b)为采用原SUSAN算法检测的图像,检测出611个角点,图 7(c)为按Y(r0)值排序取所有角点的图像,图 7(d)为按ri值排序取所有角点的图像。结果显示,使用该方法可有效保留“好”的角点,并使角点均匀分布在图像上,有利于角点的匹配[8-10]。

图7 算法验证实验图像
4 结论
图像匹配中角点的快速检测算法研究对于计算机视觉和图像处理有重要的理论和实践意义,但目前主流的角点检测算法均存在一定的缺陷。本文针对基于SUSAN算法的分层快速角点检测算法存在的计算量大、无法满足实时性等缺陷,提出评价角点“性能好坏”的判定函数和由粗到细的检测算法。实验结果证实:改进的算法可大大缩短运算时间,提高实时性,同时使图像匹配效果也有较大改善。
[1]张法全,陈良益,何俊华,等.基于VC和GPIB的数字示波器远程控制[J].微计算机信息,2007,23(28):103-104.
[2]Wurtz R P,Lourens T.Corner detection in color images by multiscale combination of end-stopped cortical cells[C]//ICANN.London:Springer-Verlag,1997:901-906.
[3]李俊平,周振环.提取图像边界角点的新方法[J].微电子学与计算机,2006,23(11):188-199.
[4]Harris C,Stephens.A combined corner and edge detecter[C]//Matthews M M.Processdings of the 4th Vision Conference.Manchester the University of Sheffield printing Unit,1998,147-151.
[5]Trajkovic M,Hedley M.Fast corner detection[J].Image and Vision Computing,1998(18):75-87.
[6]Tang B D.Jamel A B,Bogdan J M.An efficient feature based matching algorithm for stereo images[J].Proceedings of the Geometric Modeling and Imaging IEEE,2006,90(4):72-75.
[7]赵锋伟,李吉成,沈振康.景象匹配技术研究[J].系统工程与电子技术,2002,24(12):110-113.
[8]罗钟铉,刘成明.灰度图像匹配的快速算法[J].计算机辅助设计与图形学学报,2005 (5):966-970.
[9]姜 凯,陈海霞,汤建华.一种快速图像匹配算法的设计与实现[J].计算机工程与应用,2004,87(3):87-89.
[10]王岩松,阮秋琦.一种基于互相关的图像定位匹配算法研究及应用[J].北方交通大学学报,2002,26(2):20-24.
