交叉口Agent 间的博弈学习协调方法
2010-08-16夏新海许伦辉
夏新海,许伦辉
(1.华南理工大学土木与交通学院,广东广州510640 2.广州航海高等专科学校港航管理系,广东广州510725)
Agent是能够实时地、动态地、自主地与不断变化着的外部环境进行交互的智能规划控制系统,它可以感知并作用于环境,并且具有希望通过行为的执行而达到一定的目标。Multi-agent system是指由一组具有一定资源和能力、相对独立、相互作用的Agent组成的系统。Multi-agent system的协调是指每个自主Agent对其目标、资源、思维状态等进行合理安排,以调整各自的决策和行为,最大限度地实现各自目标。协调研究是Multi-agent system研究的核心。目前已经有一些对于Multi-agent system的协调的研究,如李凡长[1]提出了Multi-agent system的一些协调组合设计模型,包括Agent拉丁方矩阵理论等;王立春[2]利用协商-协商过程-协商线程的概念建立了一个多边-多问题协商模型,并且支持Agent在协商过程中的学习。总体来说,目前对于Multi-agent system的协调模型主要用到BDI模型,协商模型,自协调模型、协作规划模型等。主要的协调方法主要涉及到基于对策论的显式协调和基于社会规则的隐式协调,以及用到一些学习方法。
目前基于Multi-agent的协调在开放、分布、复杂系统中得到广泛的应用。以城市交叉口系统为例,城市交叉口系统在具有分布式、多干扰、不确定性特点的同时,又具有很强的自组织、自学习、自稳定的特点;而Multi-agent system具有分布式结构、很强的自学习自组织能力,同时又具有相互间的协调功能,与城市区域多交叉口系统在结构上、机理上具有很大的相似性,因此将基于Multi-agent的协调在城市交叉口协调控制中的应用已经受到国内外越来越多的重 视。Burmeister 和 SUSAN[3-4]提 出 了 Multiagent在交通运输中应用的思路;欧海涛[5]提出了一种基于递归建模的多智能体协调方法及多智能体的贝叶斯学习方法并应用于城市交通系统中;马寿峰[6]采用对策论与社会规则相结合的方法实现了两个路口控制Agent间的协调问题。总的来说,Multi-agent应用在城市交叉口协调时在协调模型、方法、机制等方面的研究还不够。笔者将 Multiagent技术应用在城市交叉口的协调控制中,建立一种基于Multi-agent的协调机制,并用分布式Q学习方法和对策论作为其实现策略,验证了基于Multiagent的城市交叉口信号协调方法的有效性。
1 基于Multi-agent的协调机制
1.1 Agent间的协调过程
以城市交叉口协调为例,城市区域内各交叉口处的交通流是相互关联的。为每个交叉口设立一个Agent,称为路口 Agent。路口Agent之间是平等自治的关系。每个自治的路口Agent代表一个路口的利益。设立一个管理Agent负责若干个路口Agent的协调管理。路口Agent和管理Agent统称为TSCA(Traffic Signal Control Agent)。路口Agent主要由学习器、行为决策器、通讯模块、协调模块组成。学习器根据实测的交通数据判断是否有符合条件的规则,如果有,则执行该规则,从而确定信号控制方案。协调模块则负责分析路口Agent所控路口目前的交通状态,决定是否有必要向其它路口Agent发送消息,并处理路口Agent间的协调问题。通讯模块主要负责与管理Agent及相邻路口Agent的通讯,行为决策器主要解决路口Agent的推理决策功能。基于Muli-agent的城市交叉口协调控制主要通过TSCA的协调达到交通流信号控制的最优化。
路口Agent和管理 Agent间的协调过程如下(通过引入拥挤度阀值):①如果路口Agent某相位的拥挤度没有超过阀值,则路口Agent可以采用自主式信号控制;②当路口Agent某相位的拥挤度超过了阀值,则路口Agent需要与相邻的路口Agent进行交互;③若协调策略存在,每个路口Agent按照该协调策略进行信号控制,本次交互结束;如果协调策略不存在,则与上一级管理Agent进行交互;④管理Agent对其所辖的路口Agent进行协调,寻求协调策略;如果管理Agent对其所辖的路口Agent协调失败,则与相邻的管理Agent进行交互,寻求协调策略,否则,各个路口Agent按照原策略进行控制。
1.2 资源动态协调配置模型
城市交叉口协调中存在资源冲突、目标冲突、结果冲突等,由于城市交叉口间的交通流具有较强的关联性,单独追求某一交叉口通行能力的提高和延误的减少而不考虑路口之间的相关性,可能引起关联路口更大的延误。
对于单交叉口Agent,设Q(n-1)p为在第n-1个周期,p相位绿灯信号末该方向车辆滞留数;qkp为p相位第k秒到达的车辆数;off-c为交叉口驶离率;tpg为 p相位绿灯时间,则有[7]:
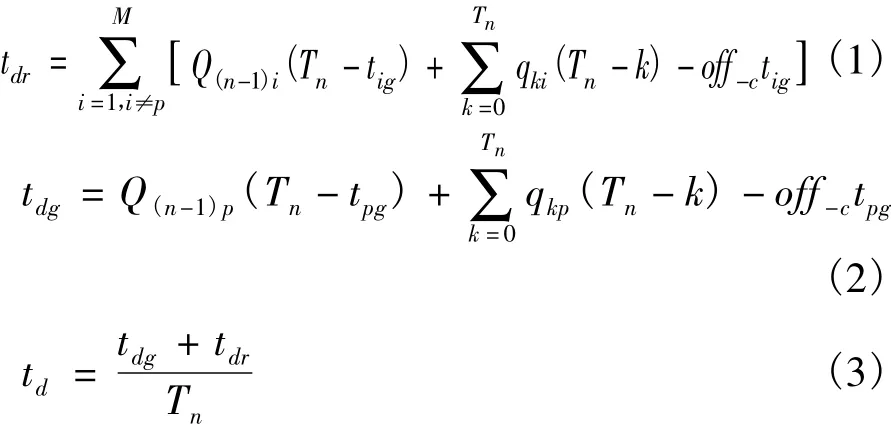
式中:tdr为当前相位红灯方向车辆排队等待时间;tdg为从上一周期该相位绿灯信号结束到当前时间内绿灯方向车辆排队等待时间;td为平均等待时间;Tn为信号周期时间长;M为相位数。
这里以一个TSCA为一个角色,对第i个区域内包含n个关联的角色TSCA的资源协调配置可以抽象表示为[8]:
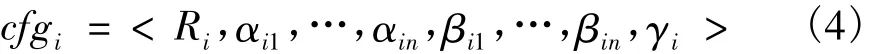
式中:Ri为资源描述,包括资源价格,这里可以选为某一区域交叉口单位时间通行能力的提高额度或者延误的减少程度;αi1,...,αin为 n个 TSCA所需要的资源份额,这里可以选为各个路口通行能力的提高额度或者延误的减少程度;βi1,...,βin为 n个TSCA所承担的空闲资源份额;γi为空闲资源占总资源的份额。
设 raij表示某一角色 TSCA,αij>0,βij≥0 ,并满足
定义:当 βij=0 时,d(βij,0)=0;当 βij>0 时,d(βij,0)=1 。
当对资源的需求发生变化时,设一次协调只能有一个TSCA需要的资源份额发生变化。设角色TSCA rain需要的资源发生变化,αin≠α′in,则:
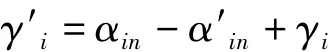
rain对空闲资源的承担,要么 β′in=βin,保持不变;要么随需求变化采用公式(5):

对其它角色TSCA raij,j=1,…,n-1 ,若βin=1 ,则 β′ij=βij=0,否则由式(6)计算,保持彼此间相对份额不变:
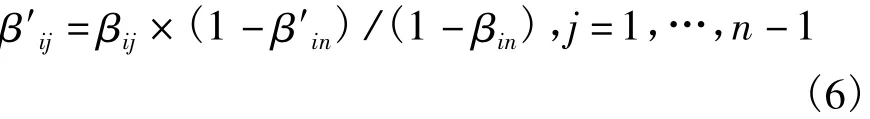
对于不承担空闲资源的角色TSCA,调整后依然无需承担空闲资源开销,即如果βij=0,则β′ij=0,j=1,…,n。
2 Agent间协调实现方法
对策论是研究人类社会交互的最佳数学工具,许多学者应用对策论进行多Agent系统中协调的研究。这里采用对策论和分布式Q-学习方法相结合来实现Agent间的协调。
2.1 基于对策论的协调的实现
以城市交叉口协调为例,TSCA间的对策协调方法可以描述为一个4元组
2)A为交通实体所有可能的策略或者行动的集合,A=C(m)×S(n),则A中一共有m×n种执行策略组合。
C(m)为调整策略,m为C中策略个数,如取C(m)={红灯时间加4 s,红灯时间加8 s,红灯时间减4 s,红灯时间减8 s,保持不变};
设S(n)为行动策略,其值由路口相位决定,n为S中策略个数,以四相位路口为例,可以取S(n)={东西直行及右转,南北直行及右转,东西左转,南北左转相位}。
3)U为TSCA所获得的效益。经常用到的计算利益的指标有车辆延误时间、车辆停车次数等,采用1.2的Q值,Q值大小反映行为策略的优劣。
4)I表示每个TSCA拥有的信息,包括其他TSCA的特征和行动策略信息。
此协调途径中,每个TSCA依据它所拥有的信息I,在S中选择合适的策略,通过不断的交互,则协调策略为纳什均衡策略,即:
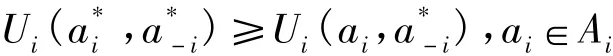
2.2 对策论的协调方法中效益函数U的确定
分布式Q强化学习算法适合用于TSCA间的协调的实现,具备一定的全局优化的特征,收敛速度快,能对整个交通网络具有较好的优化能力。TSCA间对策过程中U值大小应该能够反映TSCA选择不同行为策略所带来的效益,而分布式Q学习算法中Q值大小反映策略的优劣,所以取U=Q。据英国运输与道路研究所研究成果,只要围绕每个TSCA与其相邻TSCA协调能够取得一个接近整体最优的效果,那么整个路网的协调效果也是接近“整体最优”。同时为了避免随着被控路网路口数量的增加而导致TSCA之间的协调过于频繁和复杂,限定每个TSCA只跟与其相邻的TSCA进行协调。因此,这里采用的分布式学习算法中每个TSCA通过与其相邻TSCA上次交互信息的历史学习来获得其相邻TSCA的奖惩函数值,对值函数进行更新。分布式Q学习中各TSCA利用其相邻TSCA的奖惩函数信息来更新值函数[9-12]:

式中:αi∈[0,1]为 TSCAi的学习速率;γi∈[0,1]为TSCAi的折扣因子;Ai为TSCAi所有可供选择的行为的集合;si为TSCAi交通流环境的当前状态;s′i为TSCAi交通流环境的下一个状态;n为TSCAi相邻的所有其它TSCAi的数目;Qi(si,ai)为TSCAi的 Q 值函数;Qi(s′i,a′i)为 TSCAi在下一个状态 s′i选择行为a′i的 Q值函数;ri(si,ai)为TSCAi的奖惩函数;rj(sj,aj)为与TSCAi的相邻的TSCAj的奖惩函数值(如果TSCA当前决策经过一定的通行时间之后先前的拥堵得到改善,奖惩函数r>0,对刚才的决策进行奖励,TSCA在以后类似的交通状态下会选择这种行为策略;否则进行惩罚,将通行权切换给其它相位);f(i,j)为TSCAi依赖TSCAj的奖惩函数值程度的影响权值函数(如下游交叉口的交通压力大于交叉口的交通压力,此时相邻下游交叉口j的奖惩值对交叉口i的影响将增加,从而协调本TSCAi的行为决策,从而缓解下游交叉口交通压力)。
根据Q值进行行为选择时,根据文章1.1对策论方法求解Nash均衡,作为Q学习策略选择的依据。
3 在城市交叉口协调中的应用分析
交叉口各个路口的到车状况事先无法知道,必须预测。以主干道相邻两交叉口协调为例,两个交叉口的信号均采用4个相位控制(分别为东西直行及右转,南北直行及右转,东西左转,南北左转相位),以第2个交叉口东向入口,第2个交叉口Agent通过与第1个交叉口Agent进行协调,得到上个周期第1个交叉口的到车状况。设分别为第n个周期、第2个路口东向左转、直行和右转车道的预测车数。sn1ijk为第n个周期末、第1个路口、第i个相位、第k个方向、第j个车道离开的车辆数,为路口左、直、右的预测分流比,于是有:
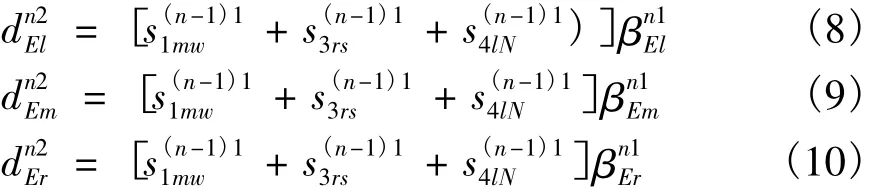
这里以主干道相邻两交叉口协调进行分析,两个交叉口的信号均采用4个相位控制(分别为东西直行及右转,南北直行及右转,东西左转,南北左转相位),路口各个方向(左,直,右)的预测分流比为0.2,0.4,0.4,车辆的到达服从随机分布,单位时间内路口放行的车辆数为2 veh/s,两交叉口间距为500 m,学习算法的学习速率为0.1,折扣因子为0.95,饱和流量为1 800 veh/h,最大排队长度为40 veh,各个相位最大绿灯时间105 s,最小绿灯时间15 s,黄灯时间1 s,全红时间1 s,车辆平均启动时间2 s。采用本文的有协调和无协调方法的计算结果如表1。
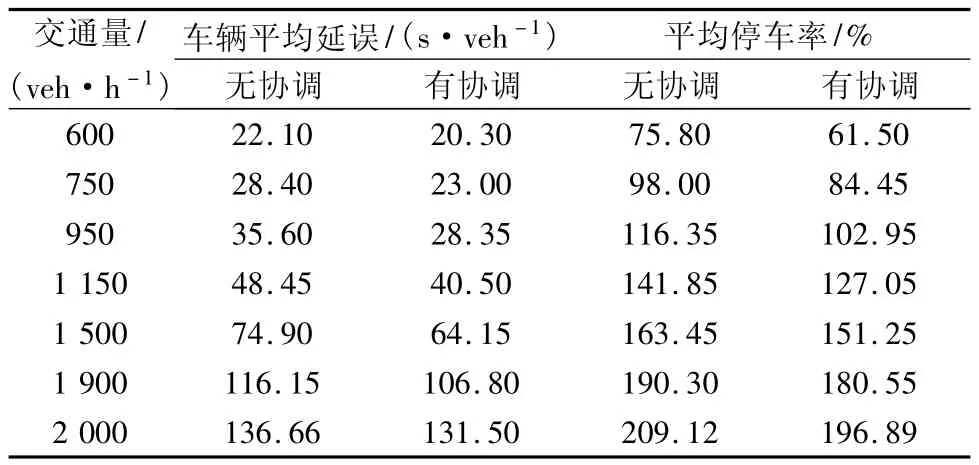
表1 区域交叉口协调效果对比Tab.1 The comparison of the coordination results
随着交通量的增大,总的车辆平均延误和平均停车率逐渐增大,但在交通量相同的时候,有协调方法要比无协调方法明显降低。当流量增加到超过饱和流量时候,协调方法改善逐渐减弱,则必须在更多的相关联的交叉口之间寻求协调。
4 结论
通过比较城市交叉口系统和Multi-agent system的相似性,引入交通信号控制 Agent,分析了Agent的协调过程,建立一种基于Multi-Agent的城市交叉口资源配置动态协调模型,应用了对策论作为协调实现途径,并且以分布式Q强化学习中Q值更新作为其效用函数。通过对两交叉口协调实例分析,车辆平均延误和平均停车率均减少,证明了采用该协调方法的有效性。
[1]李凡长.Agent的协调组合设计模型研究[J].小型微型计算机系统,2002,23(2):246 -249.
[2]王立春.多 Agent多问题协商模型[J].软件学报,2002,13(8):1637-1643.
[3]Burmeister B,Haddadi A,Matylis G.Application of multi-agent systems in traffic and transportation[J].IEEE Proceedings on Software Engineering,1997,144(1):51 -60.
[4]Susan E L.Issues in multi- agent design systems[J].IEEE Expert Intelligent Systems& Their Application,1997,12(2):18-26.
[5]欧海涛.基于RMM和贝叶斯学习的城市交通多智能体系统[J].控制与决策,2001,16(3):291 -295.
[6]马寿峰.一种基于agent协调的两路口交通控制方法[J].系统工程学报,2003,6(3):273 -278.
[7]黄艳国,许伦辉,邝先验.基于Multi-agent协调的区域交通信号优化控制[J].江西理工大学学报,2009,30(1):50-52.
[8]石纯一.基于 Agent的计算[M].北京:清华大学出版社,2007:102-106.
[9]李英.多Agent系统及其在预测与智能交通系统中的应用[M].南昌:华东理工大学出版社,2004:154-158.
[10]Roozemond D A,van der Veer P.Usability of intelligent agent systems in urban trafficmanagement[J].Application of Artifical Intelligence in Engineering,1999(7):15 -18.
[11]沙志仁,黄敏.道路交叉口指路标志定量分析指标及方法研究[J].重庆交通大学学报:自然科学版,2009,28(5):926-929.
[12]夏新海,唐德华.集装箱码头物流作业Agent间的重构[J].重庆交通大学学报:自然科学版,2009,28(4):775-779.
