小直流电容三相变换器新型调制技术的研究

王树文

（东北农业大学电气工程系，哈尔滨 150030）

1 引言

三相 PWM变换器在许多工业领域内（如电动机变频调速[1-3]、不间断电源、无功补偿器等）被广泛应用。目前，传统交直交电压源变换器的直流侧电压均为理想的无波动直流电压，通常在直流侧采用具有冲击负载特性的大容量电解电容元件。大容量电解电容的使用，一方面使变换器占用空间大、成本高、响应速度慢，使系统功率因数降低，使网侧电流畸变率增大[4-7]。同时，给网侧带来谐波电流、谐波电压污染以及额外的无功消耗，不仅会降低系统自身运行的效率，而且会给负载带来很多不良影响；另一方面在能源短缺特别是金属类不可再生资源严重短缺的今天，不符合发展的方向。

基于以上分析，本文从主要制约因素即大容量电解电容元件着手探索提高交直交电压源变换器综合性能的方法，提出了新型交直交电压源变换器即小电容交直交电压源变换器。小电容元件的使用，虽然克服了大容量电解电容的使用所带来的不足，但是同时也产生新的不利影响。一方面变换器连接阻感负载时会使其输出电压中的低次谐波增大，一方面变换器连接电动机负载时会使其输出电压产生误差，同时也会使直流侧产生过电压，另外容易使网侧与直流侧产生谐振。为了向负载提供高质量的电能，对于电压源变换器来说，有效地消除输出电压的谐波成分是非常重要的[8-14]。

所以，针对交直交电压源变换器中使用小电容时出现的问题，本文着重研究了适用于小电容三相变换器的新颖调制技术即可调调制波脉冲宽度调制技术（AMW-SPWM）。该研究内容的提出旨在摈弃传统变换器中不可缺少的大容量电解电容元件，在保证负载端电能质量的同时显著改善变换器的输入谐波特性，并且对于提高变换器自身集成度和可靠性等方面也具有积极意义。

2 可调调制波脉冲宽度调制技术理论推导

传统的变换器选择标准的三相正弦波作为调制波，以A相为例，调制波的表达式如式（1）

式中，UB为标准正弦波的幅值，ω是标准正弦波的角频率，θ是正弦波与脉动直流输出电压之间的相位差，载波信号为双极性三角波。经式（1）调制后，a相电压如式（2）所示

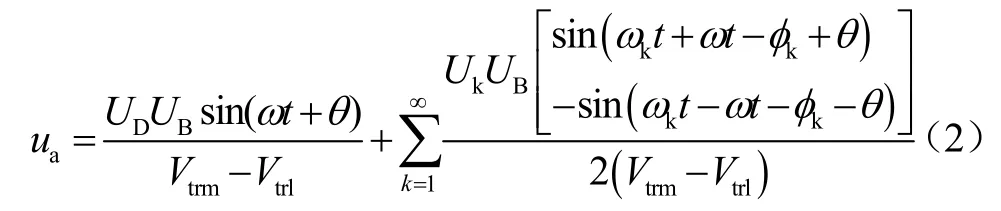
从以上分析中，可知ua的谐波分量的幅值与相位只与三相不可控整流桥输出直流电压udc和调制波us1有关，由此可得到ua和udc满足以下关系式，如式（3）所示

式中，T(θ)是逆变器触发脉冲的开关函数，可以得到开关函数的表达式，如式（4）所示

从式（4）可知，可以改变标准的调制波就可以抵消直流侧电压的波动对变换器输出电压产生的谐波的影响。基于以上观点，提出一种新的调制波，假设调制波的表达式如式（5）所示

新的调制波是两部分组成，一部分是f(t)，另一部分是us1。如把式（5）作为调制波，根据以上分析则开关函数T(θ)将为式（6）

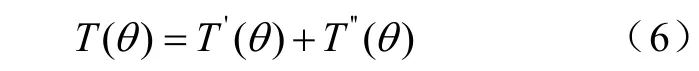
式中，T'(θ)是当调制波为us1时的开关函数，T''(θ)是当调制波为f(t)时的开关函数。

采用新的调制波之后，ua的谐波将被去除掉。ua的表达式将为

由上式可以推出T''(θ)，如式（8）所示

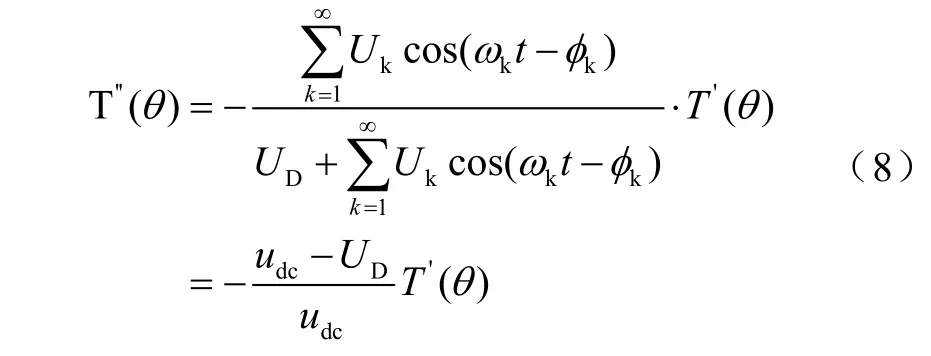
在上式中T'(θ)=T(θ)，可推得

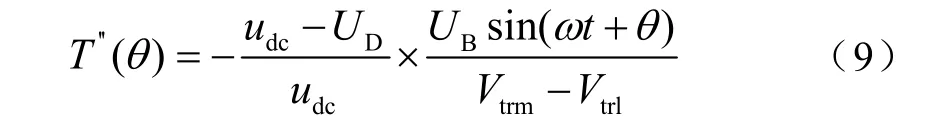
T''(θ)与T'(θ)相比较，通过相似理论可以得到k的表达式，如式（10）

因此，当采用新的调制波us进行调制，则ua在低频带仅含有基波分量，ua的表达式为

可以看出，采用新的调制波，可以消除式（2）中的谐波，得到了理想的输出电压波形，从而达到了避免在直流侧使用大电容进行滤波的目的。

3 仿真结果

为了证明采用可调调制波脉冲宽度调制技术的小直流电容三相变换器输出电压谐波小、系统侧电流畸变率小等特点，做了相应的对比实验，实验中所用的参数为：三相星接感性负载，每相电感与电阻串联，参数为 L=3.24mH ，R=1.1Ω ，直流电容10uF，系统 a相电压峰值：32V；系统b相电压峰值：31V；系统c相电压峰值：32V；载波频率：ftr=10kHz；标准正弦波峰值：UB=0.46V；三角波正峰值：Vtrm=1V，三角波负峰值：Vtrl=-1 V；标准正弦初相位：θ=0°；fsin=50Hz 。

图1-2分别给出了采用可调调制波生成方法及传统调制方法逆变器输出的电压频谱。

4 结论

可调调制波SPWM调制技术能有效地消除小电容三相变换器输出电压的谐波，仿真结果表明均获得了理想的输出电压波形和较好的频谱特性，证明了小电容三相变换器及其调制技术的优越性。

图1 传统的SPWM技术ua的波形和频谱

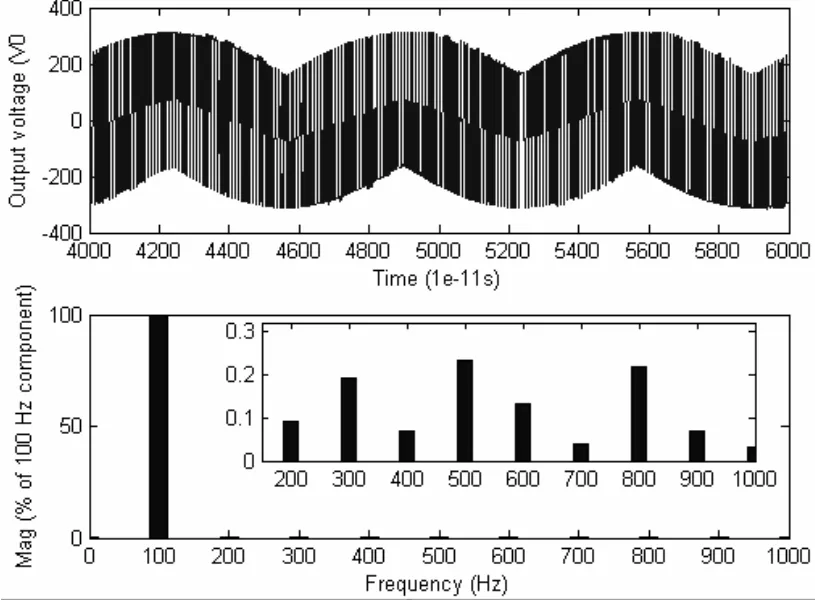
图2 可调调制波SPWM技术ua的波形和频谱

[1]Habetler T G. A space vector-based Rectifier Regulator for AC/DC/AC Converters [J]. IEEE Trans. On Power Electronics, 1999,8(1):30-36.

[2]Hur Namho, Jung Junhwan,Nam K wanghee. Fast Dynamic DC-link Power balancing Scheme for a PWM converter-inverter System[A].IECON’ 99 Proceedings[C].The25thAnnual conference of the IEEE,1999(2):767-772

[3]Jung Jinhwan, Lim Sunkyoung, Nam Kwanghee. A Feed-back Linearizing Control Scheme for a PWM Converter–inverter Having a very Small DC-link Capacitor[J].IEEE Trans. on Ind. Appl., 1999,35(5):1124-1131.

[4]周晓霞,刘星桥.一种新颖的变步长自适应谐波电流检测法[J].电力电子技术,2008,42(11):13-14.

[5]程汉湘,尹项根.SVG的直流电容选择分析[J].电气传动,2004(3):34-39.

[6]王立欣,张宁,靳刚. VSR直流侧滤波电容的计算及实验分析[J].哈尔滨工业大学学报,2006(1):63-66.

[7]林新春,刘方锐,张宇,康勇.UPS中直流电容电压纹波分析与抑制[J].电力电子技术, 2007(7):53-55.

[8]D.Shen,P.W.Lehn.Fixed-frequencyspace-vector modulation control for three-phase four-leg active power filters[J].IEE Proc.-Electr. Power Appl., 2002,149(4).

[9]Wang Hao,Zhang Chao,Yang Geng,Du Ji-hong. Detective and Close-loop Control Methods for Selective-Harmonic-Compensation Active Power Filter[C]. The 4th International Power Electronics and Motion Control Conference, August 14～16, 2004: 206-209.

[10]Li Li, D.Czarkowski, Yaguang Liu, P.Pillay.Multilevel Selective Harmonic Elimination PWM Technique in Series-connected Voltage Inverters, IEEE Trans.Industry Applications. 2000(36):160-170.

[11]George S, Agarwal V.A DSP Based Optimal Algorithm for Shunt Active Filter under Nonsinusoidal Supply and Unbalanced Load Conditions.IEEE Trans on Power Electronics. 2004,19(6):593-601.

[12]石游,杨洪耕.带谐波补偿功能的动态电压补偿器[J].电网技术,2006(14):36-40.

[13]孙铁成,汤平华,高鹏,刘鸿鹏.一种新型全桥零电压转模PWM DC-DC变换器[J].中国电机工程学报,2006,(6):83-88.

[14]王正仕,陈辉明.具有无功和谐波补偿功能的并网逆变器设计[J].电力系统自动化,2007(13):67-71/