一种基于遗传算法的无线传感器网络覆盖模型

吕广辉 ，崔逊学 ，侯战胜

(1.江西联创通信有限公司，江西 南昌 330096；2.解放军炮兵学院 计算机学院，安徽 合肥 230031；3.南京邮电大学 计算机学院，江苏 南京 210003)

无线传感器网络WSN(Wireless Sensor Network)最早来源于军事领域，1978年，卡内基—梅隆大学就在美国国防高级研究项目组(DARPA)的资助下成立了分布式传感器网络工作组，专门研究以WSN为基础的军事监视系统。该系统是传感器技术、嵌入式计算技术、现代网络及无线通信技术、分布式信息处理技术等的综合应用。

遗传算法[1]GA(Genetic Algorithm)是模拟达尔文的遗传选择和自然淘汰生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法最早是1975年由美国Michigan大学HOLLAND J教授提出来的，它是一种基于自然选择和群体遗传机理的高度并行、随机、自适应搜索算法。GA模拟了自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象，将每一个可能的解看作是群体中的一个个体，并将每一个个体编码成字符串的形式，根据预定的目标函数对每个个体进行评价，给出一个适应值，利用遗传算子选择、交叉、变异等过程对这些个体进行组合，得到一群新个体。这一群新个体由于继承了上一代的一些优良性状，所以明显优于上一代，这样就逐步向着更优解的方向进化。

遗传算法的主要优点[2]是从代表问题可能潜在解集的一个种群开始并行操作的，而不是从一个初始点开始寻优，在一定程度上避免了搜索过程收敛与局部最优解。其中一个种群则由经过基因编码的一定数目的个体组成。初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解，在每一代根据问题域中个体的适应度大小挑选个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。

1传感器网络最大覆盖度的理想模型

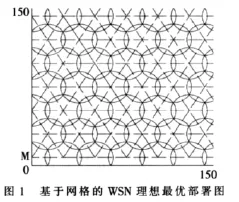
2最优部署模型节点数目公式

假设传感器的感知半径为R，被监测矩形区域的长为L，宽为W，节点的行数为 Ws，每行节点的数目为Ls，所有节点的数目为Ns。由图2可以看出，由底边向上算起，作第2行圆的下切线一条辅助线l，则底边到l的距离为：

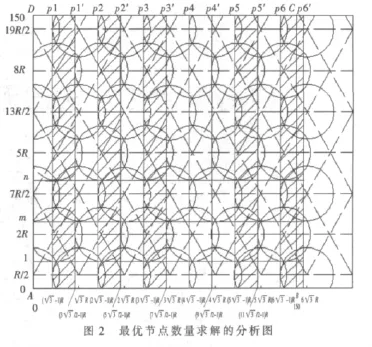
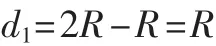
首先计算传感器节点行数，其方法为：先将切线1下面的宽度减去，然后计算1以上部分的行数，最后将1以上部分的行数加上1即为整个传感器节点的行数Ws。由图2可以看出，如果在1以上部分每行圆都作一条的下切线m、n，可以计算出相邻下切线1和m之间的距离为：

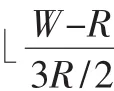
矩形每行节点的数量Ls的计算是很复杂并且不规则的，根据底边AB长度的不同，每行节点的个数是不同的。为了进行进一步判断分析，可以作出辅助线p1、p2、p3、p4、p5、p6、p1′、p2′、p3′、p4′、p5′、p6′， 如果从左边界算起，它们均是各列节点的左切线，如图2所示。从底边向上算起，p1、p2、p3、p4、p5、p6 均是奇数行中每个圆的左切线，p1′、p2′、p3′、p4′、p5′、p6′均是偶数行中每个圆的左切线。 在 p1 和 p1′、p2 和 p2′、p3 和 p3′、p4 和p4′、p5 和 p5′、p6 和 p6′之间均涂为阴影部分，如果右边还有延伸就依次类推。

根据Ws的奇偶性来计算Ns的数值：

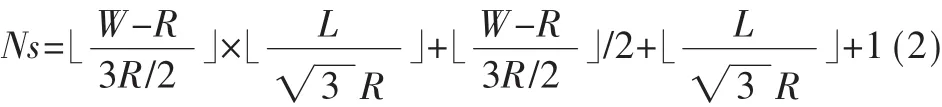
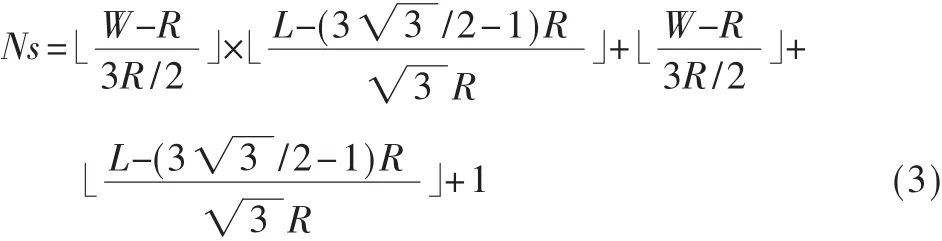
3基于遗传算法的最优覆盖策略

3.1算法网络模型

假定1：二维平面上目标被监测区域A中随机分布的传感器节点一共有n个，可以用 S={s1，s2，s3…，sn}表示所有的节点集合，si(xi，yi)表示其中的任一节点。

假定2：传感器节点是同构的，且感知模型采用布尔模型。

假定3：每个传感器的感知半径是 Rs，则任一个传感器的感知区域为以节点为圆心、Rs为半径的圆域。每个传感器的感知面积可以表示为Asi=πRs2。

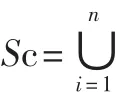
假定4：区域A内任何一个部分只要能被一个传感器节点所覆盖，则其认为是被覆盖的。

3.2算法适应度函数的求解

在监测区域A的面积和传感器的感知半径一定的情况下，要使得节点数目最少且覆盖度最大就是要使节点的分布尽量均匀，使得A内的多重覆盖的区域最小。所谓多重覆盖区域[4]就是区域被两个或两个以上的传感器节点覆盖(覆盖重数≥2)。因此，问题就转化为在一定的覆盖度的前提下，如果能使重叠面积最小，才能使用最少的传感器节点且分布更加均匀。将具有多重覆盖区域的面积设为So，将m个活动节点的面积相加即为展开后的总面积，则可以写作 m×Asi=mπRs2。对于监测区域A有如下公式：

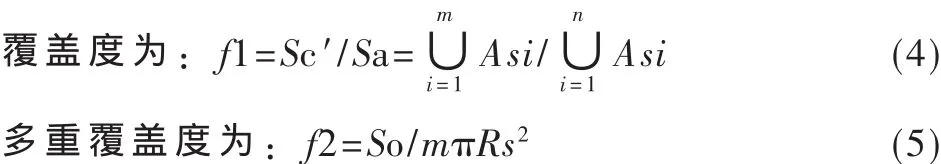
遗传算法的适应度函数[5]尤为重要，它的选择直接关系算法最后的仿真实验结果的准确性，本模型统一由式(4)和式(5)两个子函数构成，并分别加上一个权值w1、w2，保证 w1+w2=1，具体值可以由网络设计者针对网络的需要来决定。

遗传算法就是要使得适应度函数取最大值，而本文的目标是使多重覆盖度越小越好。因此对于f2函数应该取相反值，可以得到(6)的适应度函数。本文对遗传算法的适值函数F做了改进，由面积占有率的函数表达式组成，式(5)比用节点的利用率[5]表示能获得更好的效果。

4仿真实验

本实验采用MATLAB 7.0对遗传算法求解最优覆盖节点的方法进行仿真。

设监测区域为150×150的二维平面，传感器的感知半径R=15，初始群体随机部署节点个数 n=150，对于以上取值也满足算法的要求，n远大于上面所计算出的Ns的数值。基于遗传算法进行求解，交叉概率一般在[0.4，0.99]中选取，因为在优化过程中，交叉概率太大容易破坏种群中的优良模式，太小虽然容易找到全局最优解但进化的速度太慢。变异概率选取一般是要求小于0.1。考虑以上原因，实验选取交叉概率定为0.8，变异概率定为0.05，其目的就是既可以使节点最好的遗传上一代的优秀节点又防止节点出现节点局部最优而使算法过早地收敛。根据遗传算法的流程图和以上实验选取的参数因子，可以进行算法的仿真。实验中对每运行100代的相关数据(包括覆盖度、多重覆盖度、活动节点的个数等信息)都做了数据记录，图 3(a)、3(b)、3(c)、3(d)依次为算法初始状态、100、200和300代时的仿真图，图中所显示的节点均是处于活动状态节点的分布情况。本文选取运行代数为300代时作为最后的最优部署图。

有些遗传算法[6]是采用了覆盖度和节点利用率作为适应度函数，从而达到在满足覆盖度要求的前提下使节点数目最少的目的。本文利用覆盖度和节点利用率作为适应度函数做了仿真实验，在算法其他参数不变的前提下，将式(6)中以多重覆盖率作为适应度函数改为节点利用率的函数，对实验进行重新模拟，同样将实验运行到第300代，并记录了与上面实验同样的相关数据信息，分别从覆盖度和活动节点这两个数目与上面的实验做比较分析，可以得到图3(e)和3(f)的比较图。

从图 3(e)中可以看出，随着代数的增加，选用覆盖率和多重覆盖率的组合作为适应度函数要比选用覆盖率和节点利用率的组合作为适应度函数所得到的覆盖度高。并且改进前的波形曲线有时有震荡的现象，即得到的覆盖度的结果会出现不稳定的现象。改进后的波形基本接近正态分布曲线，整个实验过程很稳定，不会出现覆盖度忽高忽低的现象。

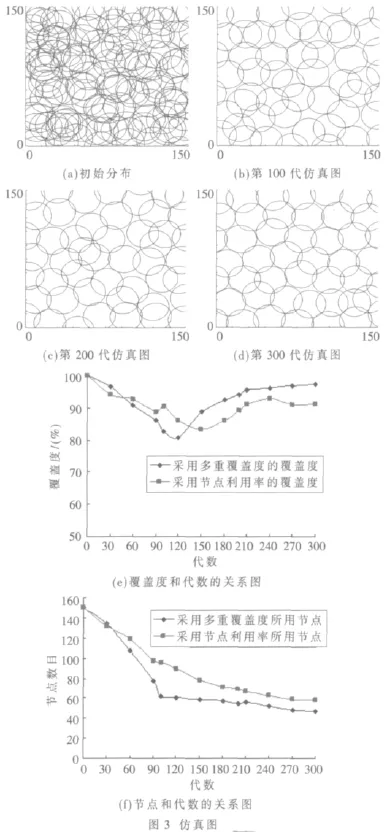
从图3(f)中可以看出，随着代数的增加，选用覆盖率和多重覆盖率的组合作为适应度函数所用的节点数目要比选用覆盖率和节点利用率的组合作为适应度函数的节点淘汰速度要快。并且到300代时，改进后的算法所用节点数目为47个，比改进前的算法所用节点数目58个要少，所以改进后的算法更加接近最优模型中节点的数目。由图3(e)、3(f)可以看出，在整个实验的过程中，改进后的算法的节点数目基本一直都小于改进前的节点的数目，即使实验运行到某一代停止了，改进后的算法依然要明显优越于改进前的算法。

本文改进的遗传算法通过以上仿真实验数据对覆盖度和节点数目的比较，可以明显地看出，本实验选用的多重覆盖度代替节点利用率作为适应度函数的遗传算法是切实可行的。也达到了所要求的在满足一定的覆盖度的前提下，减少节点利用率的实验目标。

[1]WARNEKEB， LASTM， LIEBOWITZB.Smartdust：communicating with a cubic-millimeter computer[J].IEEE Computer Magazine， 2001，34(1)：44-51.

[2]CHONG Chee-Yee， KUMAR S P.Sensor Networks：Evolution[J].Opportunities and Challenges Proceedings of the IEEE， 2003，9(8)：1247-1256.

[3]SLIJEPCEVIC S，POTKONJAK M.Power efficient organization of wireless sensor networks[C].In：Glisic S， ed.Proc.ofthe IEEE Conf.on Communications.Helsinki：IEEE Press，2001：472-476.

[4]ZHANG H，HOU J C.Maintaining sensing coverage and connectivity in large sensor networks[J].Wireless Ad Hoc and Sensor Networks， 2005，1(1)：89-124.

[5]蒋杰，方力，张鹤颖，等.无线传感器网络最小连通覆盖集问题求解算法[J].软件学报，2006，17(2)：175-184.

[6]刘华峰，金士尧.三维无线传感器网络综述[J].计算机应用，2007，27.