α稳定分布下Volterra滤波器的自适应数据块算法*
2010-08-13赵知劲郑晓华赵治栋
赵知劲,郑晓华,赵治栋
(杭州电子科技大学 通信工程学院,浙江 杭州 310018)
Volterra级数模型是非线性系统的一种输入输出模型,是线性系统脉冲响应函数模型对非线性系统的扩展。基于截断的Volterra级数模型的非线性自适应滤波,在处理非线性问题时,性能明显优于传统的线性滤波技术,近年来受到越来越多的关注,如有源噪声控制[1]、回声抵消[2]等。高阶的Volterra滤波器结构十分复杂,实现起来相当的困难,实际中通常以截断的二阶Volterra级数展开式近似非线性模型[3],即二阶Volterra滤波器。在许多实际应用中,所遇到的诸如水声、低频大气噪声以及许多人为噪声等,往往具有一定的甚至是比较显著的脉冲特性,这种噪声不符合高斯分布,而是服从稳定分布[4]。参考文献[5]提出的非线性Volterra滤波器LMP算法性能在稳定分布环境下要比传统的Volterra滤波器LMS算法性能优越。由于二阶Volterra级数模型中非线性项将稳定分布的尖峰脉冲特性更加放大,使输入信号自相关矩阵的特征值扩展更大,从而导致传统的VLMP算法收敛很慢,甚至不能正常工作。为了改善VLMP算法性能,本文将Volterra滤波器权向量的线性项部分和非线性项部分分别采用不同的收敛因子,并且利用更多的输入信号和误差信号的信息,更准确地估计梯度,提出了数据块VLMP算法(DBVLMP)。
1 传统的二阶Volterra LMP算法
一个截断二阶Volterra滤波器输入输出关系为:
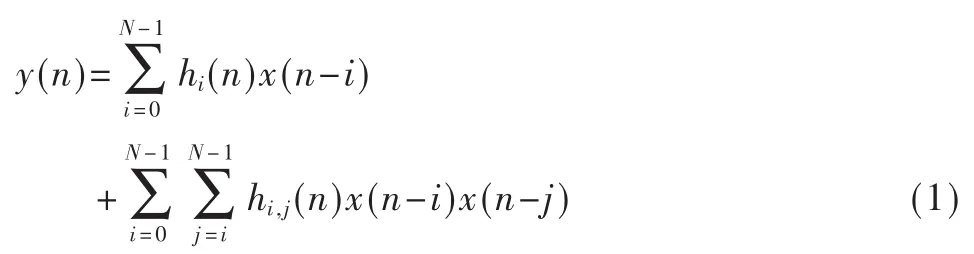
其中N是记忆长度,输入向量为:

其中,X1T(n),X2T(n)分别为线性部分和非线性部分的输入向量:
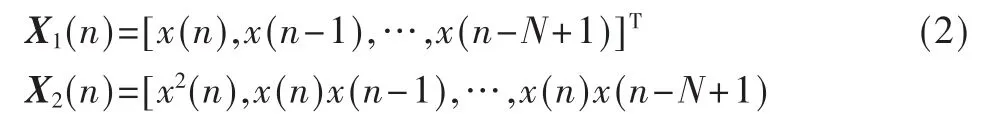

相应地,Volterra滤波器的权向量为:

n时刻线性部分的权向量为:
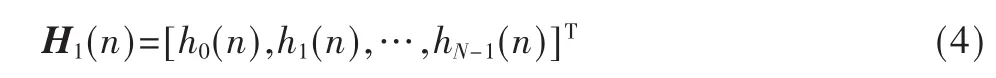
非线性部分的权向量为:

所以整个系统的输出为y(n)=HT(n)X(n)。
传统的Volterra LMP算法是将Volterra滤波器建模成一个伪线性算子,从而可以直接利用α稳定分布下线性滤波器的LMP算法,得到VLMP算法的权向量修正公式[5]:
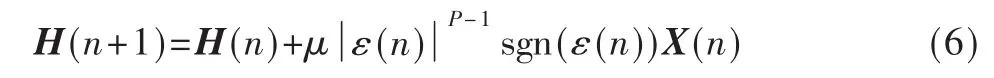
在α稳定分布背景下Volterra滤波器的非线性项将稳定分布的尖峰脉冲特性放大,导致输入信号自相关矩阵的特征值扩展更大,只用一个收敛因子同时调整线性部分和非线性部分的权值后的收敛性能仍然很不理想。
2 α稳定分布下Volterra滤波器的数据块算法
现构建由n时刻及其前m-1个时刻的输入矢量所构成的矩阵,分别表示如下:
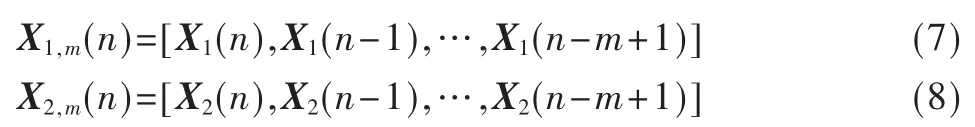
分别记 D(n)和ξ(n)为由n时刻及其前m-1个时刻的期望输出矢量和相应的误差矢量,表示为:

则误差矢量ξ(n)可以表示为:
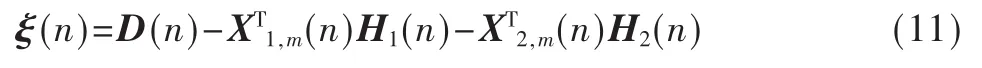
在α稳定分布下,基于最小分散系数(MD)准则[4]的代价函数为:

以误差信号的瞬时值代替其统计平均,得到梯度估计[6]为:


sign()=[sign(ε(n)),sign(ε(n-1)),…,sign(ε(n-m+1)]T由此可以得到α稳定分布下Volterra滤波器数据块LMP(DBVLMP)算法的权系数调整公式如下:

3 算法仿真与性能分析
在α稳定分布环境下,将本文算法应用于非线性系统辨识。非线性系统期望输出信号为:
d(n)=0.7x(n)+0.4x(n-1)-0.5x2(n)+0.1x2(n-1)-0.2x(n)x(n-1)+v(n),其中,v(n)为特征指数为 α、分散系数 γ为1、对称参数和位置参数均为0的α稳定分布(称为标准对称α稳定分布)噪声,输入信号x(n)=0.5x(n-1)+s(n),s(n)为均值为0的高斯噪声。令 var_x为x的方差,定义广义信噪比为),设 GSNR=30。 用权系数误差范数如式(16)所示分析算法的收敛性能。每条曲线由20次独立实验求平均得到。

实验一:比较m=1时的DBVLMP算法和VLMP算法。特征指数α=1.8标准对称α稳定分布环境中权值h0曲线和权系数误差范数曲线如图1和图2所示。

图1 α=1.8,权值h0收敛曲线
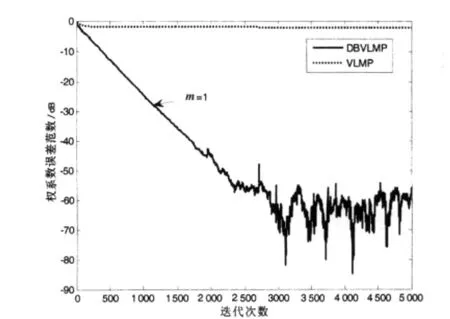
图2 α=1.8,两种算法误差曲线
m=1时,DBVLMP算法退化为一般的采用2个收敛因子分别对线性部分和非线性部分进行调整的改进型VLMP算法。由图1可知,m=1时的DBVLMP算法权值h0能快速稳定地收敛,而VLMP算法不能正常工作;从图2可看出,本文算法表现出了远比VLMP算法优越的性能;说明对权向量的线性项部分和非线性项部分采用不同的收敛因子可以大大改善VLMP算法性能。
实验二:在不同特征指数标准对称α稳定分布下,m对DBVLMP算法性能的影响。取不同值时DBVLMP算法权系数误差范数曲线和权值的仿真结果如图3~图6所示。
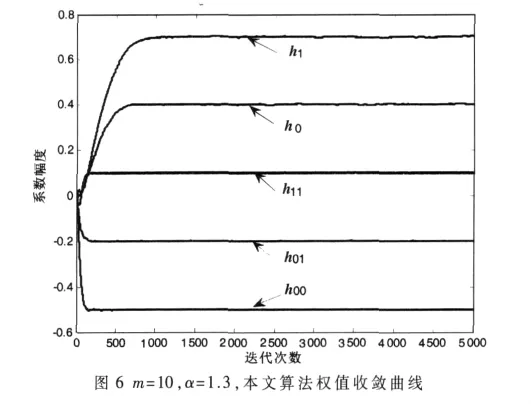
图3和图5给出了当特征指数 α=1.8和 α=1.3,m取不同数时,本文算法的权系数误差范数曲线。由图可知,随着m的增大,DBVLMP算法的收敛速度越来越快,但是这种加快的趋势在减小;m≤10时,增大m,DBVLMP算法收敛速度提高明显;m≥10时,增大 m,收敛速度提高缓慢。图4和图6所示的是取m=10时,不同特征指数下DBVLMP算法的权值的收敛曲线。由图可知,在不同脉冲噪声背景下,DBVLMP算法都能够非常快速地收敛到期望权值。同时,当算法收敛时,没有因为大幅度的脉冲噪声而出现大的抖动,这说明DBVLMP算法对脉冲噪声有较强的韧性。

本文提出了α稳定分布下Volterra滤波器的一种数据块LMP新方法,该算法分别采用不同的收敛因子,自适应调节滤波器权向量的线性项部分和非线性部分,利用了更多的输入信号和误差信号的信息估计梯度,从而获得比VLMP算法更高的滤波过程的收敛速度和精度。
[1]TAN L,JIANG J N.Adaptive volterra filters for active control of nonlinear noise processes[C].IEEE Transaction on Acoustics Speech and Signal Processing,2001,49(8):1667-1676.
[2]ZHOU Da Yong,DEBRUNNER V,ZHAI Yan.Efficient adaptive nonlinear ECHO cancellation,using sub-band implementation of the adaptive volterra filter[C].IEEE international Conference on Acoustics,Speech and Signal Processing,2006,(5):277-280.
[3]MATHEWS V J.Adaptive polynomial filters[J].IEEE Signal Processing Magazine.1991,8(3):10-26.
[4] 邱天爽,张旭秀,李小兵,等.统计信号处理[M].北京:电子工业出版社,2004.
[5]WENG Bin Wei,NONLINEAR K E.Nonlinear system identification in impulsive environments[C].IEEE Transactions on signal processing,2005,53(7):2588-2594.
[6]ZHAO Zhi Jin,DONG Ke Hai,XU Chun Yun.Data block adaptive filtering algorithms for α-stable random processes[J].Digital Signal Processing,2007,17(4):836-847.
