考虑偶应力影响的双组节理岩体等效模型

刘 俊，黄 铭

（1.上海交通大学船舶海洋与建筑工程学院，上海 200240；2.合肥工业大学土木与水利工程学院，合肥 230009）

考虑偶应力影响的双组节理岩体等效模型

刘 俊1，黄 铭2

（1.上海交通大学船舶海洋与建筑工程学院，上海 200240；2.合肥工业大学土木与水利工程学院，合肥 230009）

考虑到岩体中节理存在的影响，针对具有两组斜交节理的岩体，通过对代表单元的分析，得到了基于一般Cosserat介质理论的等效模型，该模型可以退化到岩体具有两组正交节理或一组节理的情形。将上述模型以自编程序实现，对节理岩体沉降进行了数值模拟，同时采用增设节理单元法进行了对比分析，两者具有较好的一致性，最后讨论了两组节理不同斜交角度的影响，计算结果表明等效模型合理有效。

节理岩体；Cosserat理论；等效模型；有限元分析；偶应力

1 概 述

确切了解岩土的特性以及由于工程建设（或开挖）而引起的岩体或土体应力、变形和破坏的发展规律并对其稳定性作出正确评价非常重要，而在土木、水利等工程中所接触到的岩体总是具有结构面，这些结构面的存在改变了岩体的均匀连续性。受层状或多组节理切割的岩体是岩土工程中经常遇到的，研究节理岩体的力学行为特点，建立合适的模型进行数值模拟分析对岩体工程设计和施工具有理论和实际意义。

对于节理岩体的模拟，一般有采用节理单元的显式方式［1］和建立宏观复合等效模型的隐式方式［2－5］。在节理密集时，应用节理单元进行分析相当困难和麻烦，而隐式方法将节理岩体等效为具有各向异性特点的连续体，求解非常方便，但其应用前提是等效模型必须合理有效。

绝大部分节理岩体等效模型基于传统连续介质理论构建［2－5］，传统连续介质理论建立在均质、连续的基本假设之上，所以其求解的正确及精确程度依赖于材料对均匀性假定的满足程度。事实上节理的存在使得岩体具有明显的宏观特征尺度和结构性，Cosserat介质理论由于可以考虑特征尺度影响，较一般连续介质理论更为精确且更具有一般性，在节理岩体力学特性的数值模拟中具有理论上的优越性。

目前已有一些学者基于约束转动Cosserat理论或一般Cosserat理论针对节理岩体建立了等效模型［6－9］，但大多数研究者针对的是具有一组节理的层状岩体［6，8，9］，只有少数学者采用约束转动Cosserat介质理论进行了两组节理或是多组节理情形的研究［7］。考虑到约束转动Cosserat理论中转动位移不独立，剪应力无法确定，采用一般Cosserat介质理论更为合适。

本文基于一般Cosserat介质理论，针对具有两组斜交节理的岩体，通过对代表单元的分析，建立了平面等效模型，并以有限元程序实现。随后分别采用等效模型和增设节理单元法对节理岩体沉陷进行了数值模拟，同时对两组节理不同斜交角度的影响进行了讨论，结果表明该等效模型可以有效模拟节理岩体的力学行为。

2 Cosserat介质理论

由于介质具有微结构，代表单元具有尺度，偶应力及曲率被引入，如图1。

对于平面问题，其微分平衡方程为：

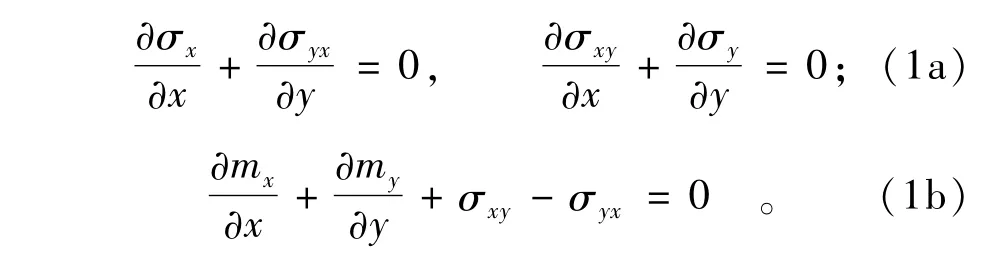
式中：σx和σy为正应力；σxy和σyx为剪应力，且σxy≠σyx；mx和my为偶应力。

几何变形方程为6个：

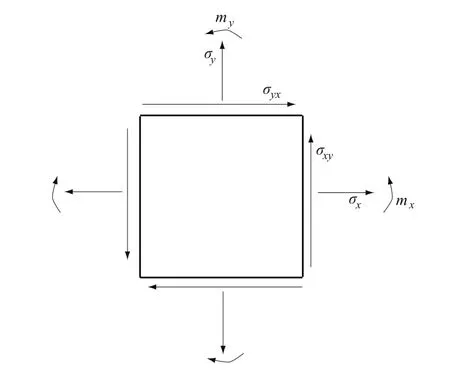
图1 Cosserat单元Fig.1 A Cosserat element

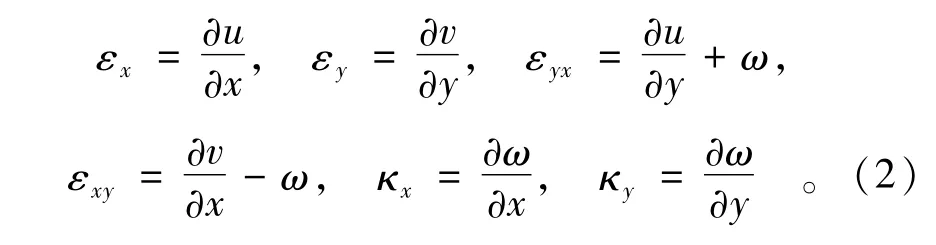
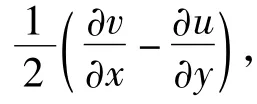
3 斜交节理岩体模型

3.1 局部坐标系下斜交节理岩体模型

考察具有两组斜交节理，节理间距分别为d1和d2的岩体。视为平面问题，则代表单元如图2。

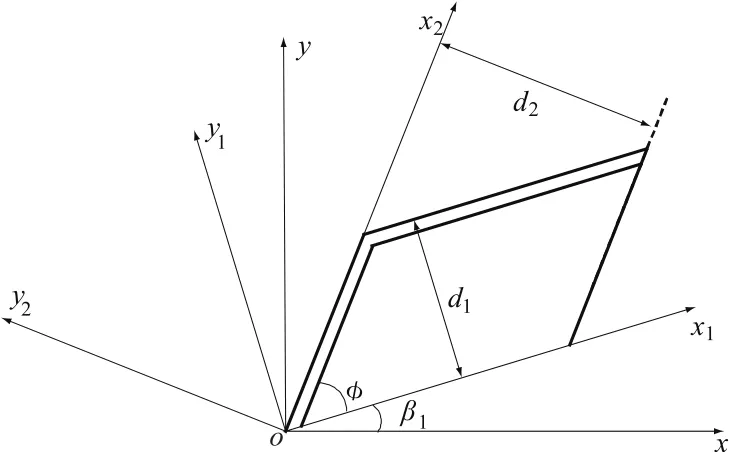
图2 2组斜交节理岩体代表单元Fig.2 An element of rockmass w ith two sets of nonorthogonal joints

图2 中，oxy为整体坐标系；局部坐标系ox1y1的x1轴在第一组节理面内，y1轴垂直于第一组节理面；ox2y2依ox1y1的相同方式定义；ø为两组节理的夹角；β1为第一组节理面和整体坐标系x轴之夹角。

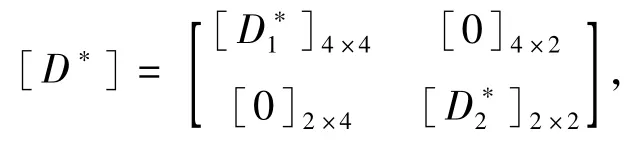
以｛σ*｝和｛ε*｝分别表示ox1y1下传统应力和应变矢量，则在ox1y1下，有｛σ*｝＝［］｛ε*｝和｛ε*｝＝［S*］｛σ*｝。在此，基于变形等效原则，可以得到［7］

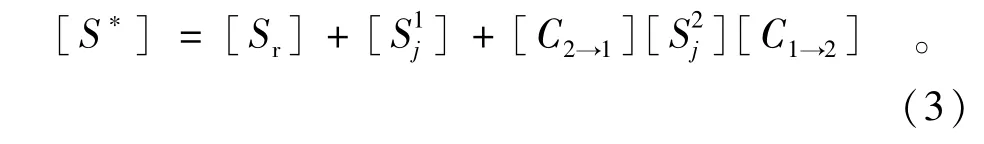
式中：［S*］为ox1y1下节理岩体性质矩阵；［Sr］是岩块性质矩阵；［］是oxiyi下第i组节理对岩体柔度性质的贡献（i＝1，2）；［C1→2］和［C2→1］为转换矩阵，且有［C1→2］＝［C2→1］T＝［C2→1］－1。其中，考虑非对称Cosserat剪应力与剪应变的关系，有

刚性执行。军队行政权力清单制度规范的内容，主要是机关部门行使的权力，一旦列入清单，该项权力就必须按照规定的权限、内容和流程行使，任何单位和个人不得随意增加和削减清单列入的权力。对未列入清单的权力，则是处于该部门职权范围之外，不得越权行使。一旦违规用权，必须严肃追究责任，承担相应后果。

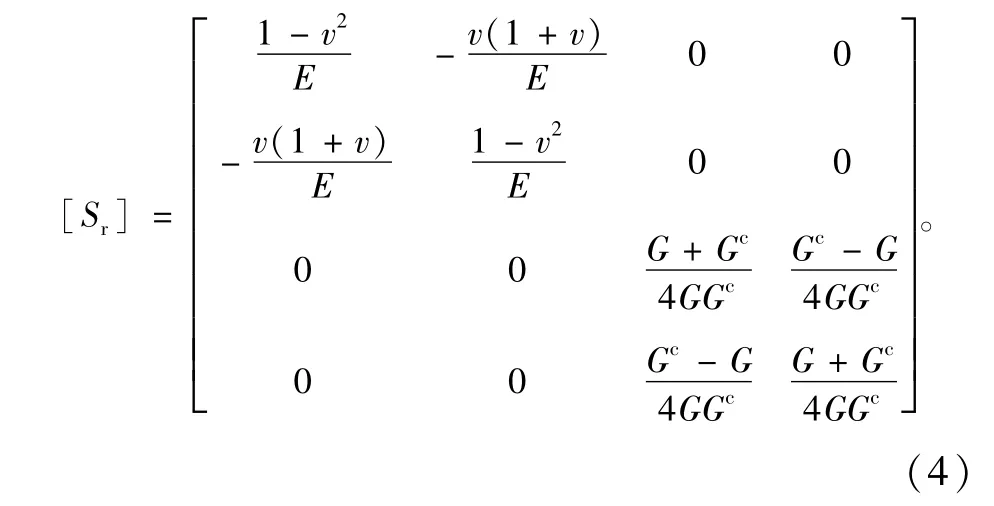
式中：E，v分别为岩块的杨氏模量与泊松比；G为通常意义下的剪切模量，Gc为Cosserat剪切模量［6］。

又有

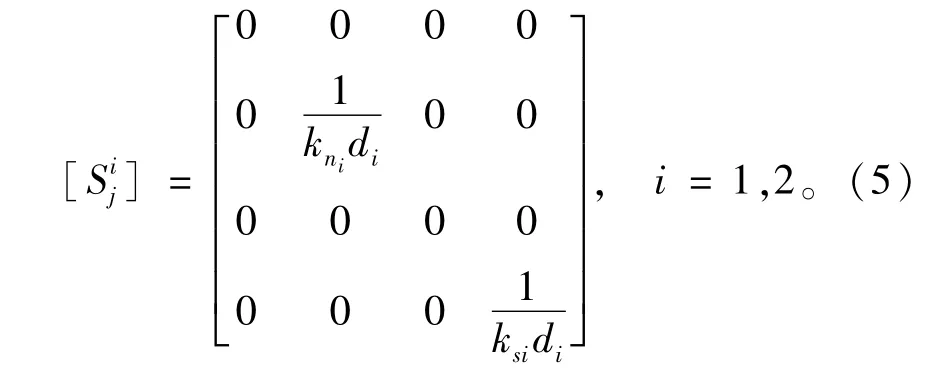
式中：kni，ksi分别为两组节理的法向刚度和切向刚度。转换矩阵［C1→2］为

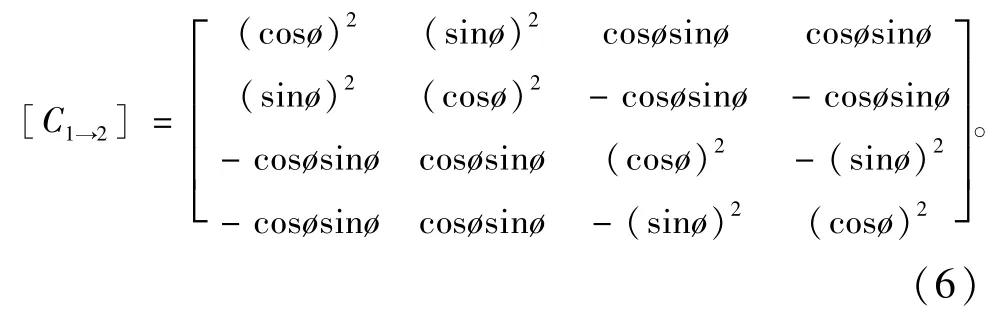
由此可以得到

分别考察节理和岩块的转角变形和外力偶的关系，可以得到

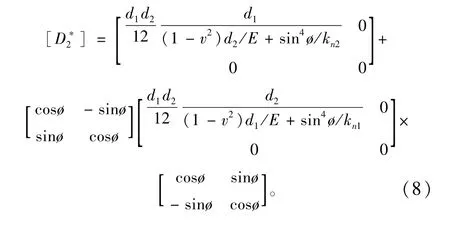
3.2 整体坐标系下弹性矩阵

通过坐标转换可以得到整体坐标系下弹性矩阵［D］为

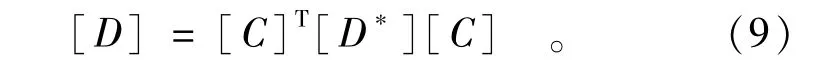
4 算 例

4.1 沉陷计算对比分析

设岩体中存在两组节理，节理面以及岩体的参数见表1。计算域尺寸6 m×3 m，上边界中部1.2 m范围作用均布载荷q＝20 kN／m。

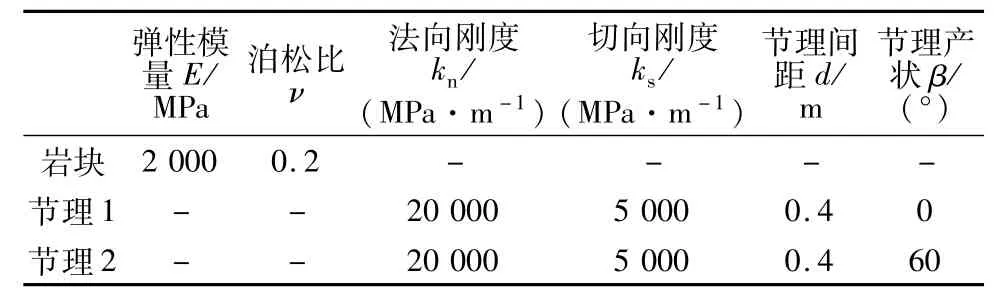
表1 岩体物理力学参数Table1 Mechanical parameters of a rockmass

分别采用本文等效模型和增设节理单元法进行分析，得到上部边界的下沉曲线如图3，可以看出中部向下垂向位移最大；受第二组节理的影响，基岩两边变形不对称，左侧的垂向位移大于右侧；同时可以发现，两者的结果具有很好的一致性，说明文中建立的等效模型有效。

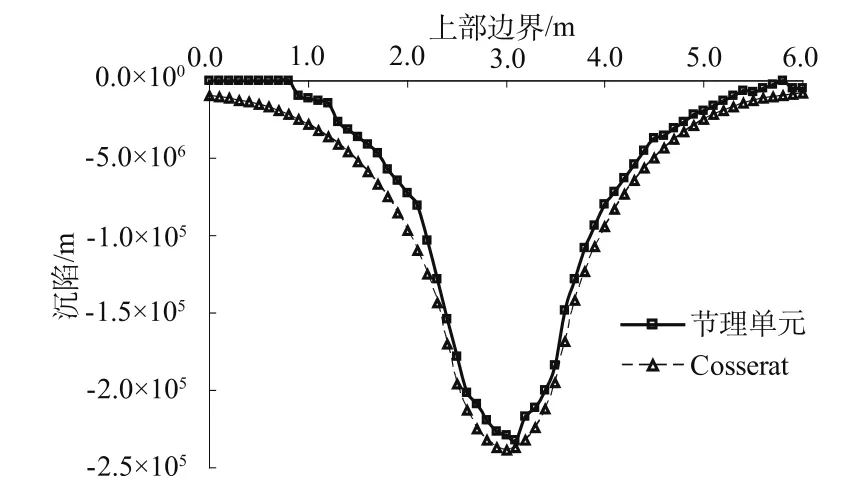
图3 上部边界的变形曲线Fig.3 Settlement curves of upper boundary

4.2 节理夹角影响

设岩体仍存在两组节理，岩块参数以及计算域和载荷同4.1。取节理法向刚度为10 000 MPa／m，切向刚度5 000 MPa／m，节理间距0.2 m。保持第一组节理水平，改变第二组节理的产状（第二组节理面与水平面的夹角分别取为0°，15°，30°，45°，60°，75°以及90°，图4为第一组节理水平，第二组节理与水平面成夹角60°的示意），考察交角变化的影响。

图4 两组斜交节理岩体Fig.4 The rockmass w ith two sets of non-orthogonal joints

计算得到上边界中部及两边的垂向位移随第二组节理角度变化的曲线见图5。从图中可以看出，夹角为15°，30°，60°以及75°时，在载荷以及约束都对称的情况下，两边变形明显不对称，岩体具有明显的各向异性；同时可以看出，模型可以反映节理产状的影响，其他条件一样时，上部沉降量会随第二组节理和水平面夹角的增大而减小，其中两组节理平行（两组节理角度都为0°）时，相当于岩体具有一组节理且节理间距为0.1m，此时沉降最大，而两组节理垂直（两组节理角度分别为0°和90°）时沉降最小，不过在这两种情况下变形都是左右对称的。

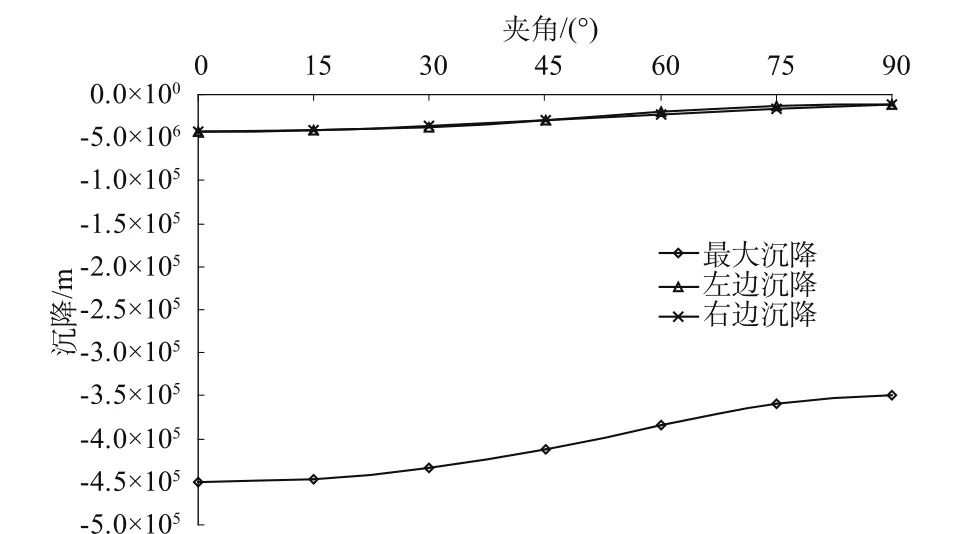
图5 变形随节理夹角变化曲线Fig.5 Settlement curves of upper boundary vs.included angles of joint

5 讨 论

本文针对双组节理岩体建立了等效模型，与增设节理单元法的对比表明该等效模型合理有效。由于实际工程中节理产状复杂，所以多组斜交节理切割岩体的力学行为分析非常重要。Cosserat介质理论相对传统连续介质理论更为精确和一般化，基于该理论进行复杂节理岩体的本构模型研究具有理论和实际工程意义，有必要进一步开展相关工作。

［1］ GOODMAN R E，TAYLOR R L，BREKKE T L.A model for the mechanics of joint rock［J］.J of Soil Mech.Found Dic ASCE，1968，94（3）：637－659.

［2］ ZIENKIEWICZO C，KELLYDW.The coupling of the finite element method and boundary solution procedures［J］.Int JNumer Methods Eng，1977，11（2）：355－375.

［3］ 张 武，张宏宪.节理岩体的弹性模型［J］.岩土工程学报，1987，9（4）：33－44.（ZHANG Wu，ZHANG Hong-xian.Elasticmodels of jointed rockmasses［J］.Chinese Journal of Geotechnical Engineering，1987，9（4）：33－44.（in Chinese））

［4］ 张玉军.节理岩体等效模型及其数值计算和室内试验［J］.岩土工程学报，2006，28（1）：29－32.（ZHANG Yu-jun.Equivalentmodel and numerical analysis and laboratory test for jointed rockmass［J］.Chinese Journal of Geotechnical Engineering，2006，28（1）：29－32.（in Chinese））

［5］ 牛 斌，杨海天.基于均匀化方法的斜交节理岩体复合本构关系研究［J］.岩土工程学报，2007，29（5）：773－778.（NIU Bin.YANG Hai-tian.Homogenizationbased investigation on constitutive relationship of oblique joint rock［J］.Chinese Journal of Geotechnical Engineering，2007，29（5）：773－778.（in Chinese））

［6］ 陈胜宏，王鸿儒，熊文林.节理岩体的偶应力有限元分析［C］∥第一届全国计算岩土力学研讨会论文集（二）.成都：西南交通大学出版社，1987：94－99.（CHEN Sheng-hong，WANG Hong-ru，XIONGWen-lin.Couple stress FE analysis for jointed rock masses［C］∥Proc.of the 1st National Seminar on Computational Geomechanics 2.Chengdu：Southwest Jiaotong University Press，1987：94－99.（in Chinese））

［7］ GE Xiu-run，FENG Shu-ren.Model of regularly jointed rockmass with consideration of the influence of couple stresses［J］.Computer Methods and Advances in Geomechanics，1991，（6）：138－152.

［8］ DAIC，MUHLHAUS H，MEEK J，et al.Modelling of blocky rock masses using the cosseratmethod［J］.International Journal of Rock Mechanics and Mining Sciences＆Geomechanics Abstracts，1996，33（4）：425－432.

［9］ 刘 俊，黄 铭，葛修润，等.层状岩体开挖的空间弹性偶应力理论分析［J］.岩石力学与工程学报，2000，19（3）：276－280.（LIU Jun，HUANG Ming，GE Xiurun，et al.Analysis on layered rockmass excavating with spatial elastic couple-stress theory［J］.Chinese Journalof Rock Mechanics and Engineering，2000，19（3）：276－280.（in Chinese））

［10］佘成学，熊文林，陈胜宏.层状岩体的弹粘塑性Cosserat介质理论及其工程应用［J］.水利学报，1996，（4）：10－17，26.（SHE Cheng-xue，XIONG Wen-lin，CHEN Sheng-hong.Elasto-visco plastic Cosserat theory of layered rockmass and its application in engineering［J］.Journal of Hydraulic Engineering，1996，（4）：10－17，26.（in Chinese） ）

（编辑：曾小汉）

Equivalent M odel of Rockmasses w ith Two Sets of Joints Considering Influence of Couple Stresses

LIU Jun1，HUANG Ming2
（1.School of Naval Architecture，Ocean and Civil Engineering，Shanghai Jiaotong University，Shanghai 200240，China；2.School of Civil and Hydraulic Engineering，Hefei University of Technology，Hefei 230009，China）

Considering the influence of existence of joints in rockmasses，an equivalentmodel has been erected based on the general Cosserat continuum theory and the analysis of a representative element.The equivalentmodel aims at rockmasses with two sets of nonorthogonal joints.Moreover，it also could be used to simulate rockmasses with two sets of orthogonal joints or one set of joint under certain condition.The equivalentmodel has been coded into a FEM program and the numerical analysis has been carried out to predict settlement of rock foundation；at the same time，the Goodman’s jointelementmethod has been applied to solving the same problem.It can be found that the deformation results obtained from abovementioned twomethods have a good agreementwith each other.Moreover，two sets of jointswith different included angles are discussed with equivalentmodel，the results show that the proposed equivalentmodel is reasonable and effective for numerical analysis in jointed rockmasses.

jointed rockmass；Cosserat theory；equivalentmodel；FEM analysis；couple-stress

TU452；O344.3

A

1001－5485（2010）09－0043－04

2009-11-26；

2010-01-14

国家自然科学基金资助项目（50609014，50979056）

刘 俊（1971-），女，湖北仙桃人，副教授，博士，主要从事岩土工程数值方法以及计算结构力学研究，（电话）021-34204470（电子信箱）JLIU＠sjtu.edu.cn。