气泡上升规律的研究与应用

杨玉阁，陈祖辉

（辽宁省水文水资源勘测局铁岭分局，辽宁 铁岭 112000）

在流量测验中，常用方法是用流速仪测取流速。半干旱地区的河流特别是小河流，水深小于0.16 m的时间长达几个月。当水深小于0.16 m时，受仪器结构的影响，规范规定要采用其它方法测取流速，现贯常采用水面小浮标法测取水面流速，而生产上需要的是垂线平均流速。所以，提出用气泡上升的过程来反映客观水流的流速情况，达到间接获取垂线平均流速的目的，进而达到精确计算流量的目的。

1 测流原理

当气泡从河底产生，受浮力作用向上运动过程中同时受到水流流动的作用，气泡产生了二维运动，即水平与垂直两个方向的分运动。由于气泡的质量极小，惯性也极小，所以当气泡在水中运动时能完全反映各层水流的运动情况。气泡由河底运行到水面的时间由水深决定；气泡运行的水平位移由各层水流的速度大小决定，水平位移是各层水流对气泡的空间累积作用的结果。由物理学理论知，平均速度等于位移与完成这段位移所用的时间的比，也就是在水文学里所要获取的垂线平均流速，即（其中v为平均流速；s为水平位移；t为气泡运行时间）。解决气泡的运行时间是一个关键问题，影响气泡运行时间的主要因素有水深和浮力。气泡在上升过程中体积变大、浮力变大、黏滞阻力变大，运动过程较复杂。通过采用实验的方法来确定运行时间与水深的关系。

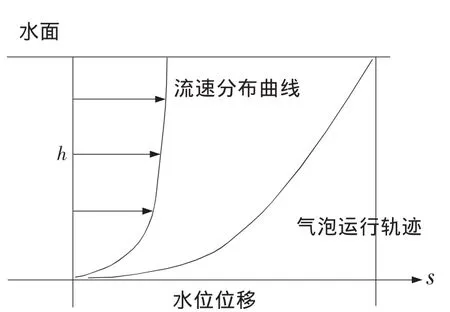
图1 气泡运动轨迹

2 气泡上升运动的实验与分析

2.1 实 验

在一个开阔的静水池中，随机选取不同的水深（考虑枯水季节水深小的特点，水深以毫米为单位），在每个水深上进行50次的气泡上升实验，记录50个时间（精确到0.01 s），取其平均值，试验成果见表1。

2.2 资料分析

以水深h为横坐标，时间t为纵坐标点绘h～t关系图。由关系曲线可以发现气泡上升的规律：当水深大于0.20 m时，关系曲线为直线，也就是说气泡匀速上升，用直线方程可以反应气泡的上升规律。当水深在0～0.20 m范围时，关系曲线为曲线，气泡上升非匀速，经过曲线拟合发现，气泡上升的规律为幂函数t=ahb形式，其中a和b为常数。将 t=ahb两边取对数得 lgt=lga+blgh，令 t′=lgt，h′=lgh，则 t′=lga+bh′为直线形式。将实验数据取对数如表2所示。

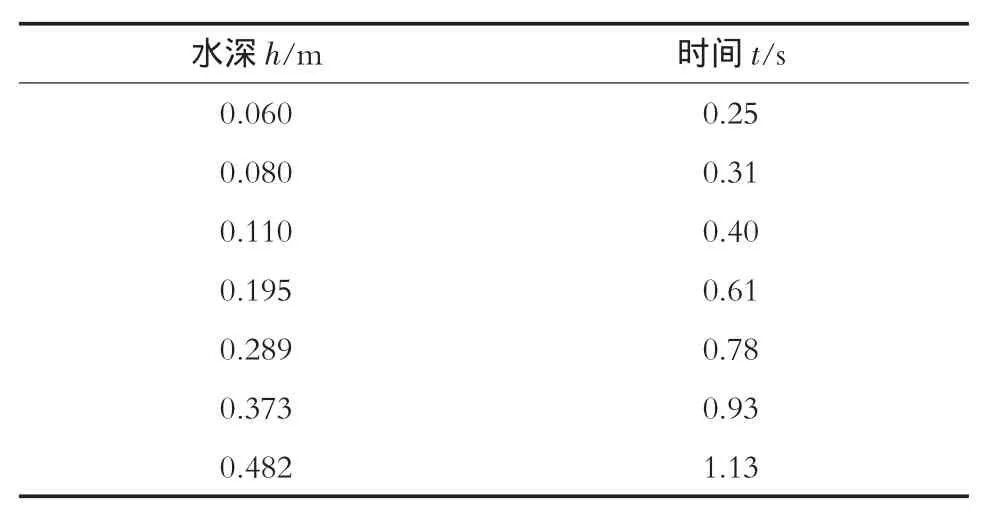
表1 试验成果表

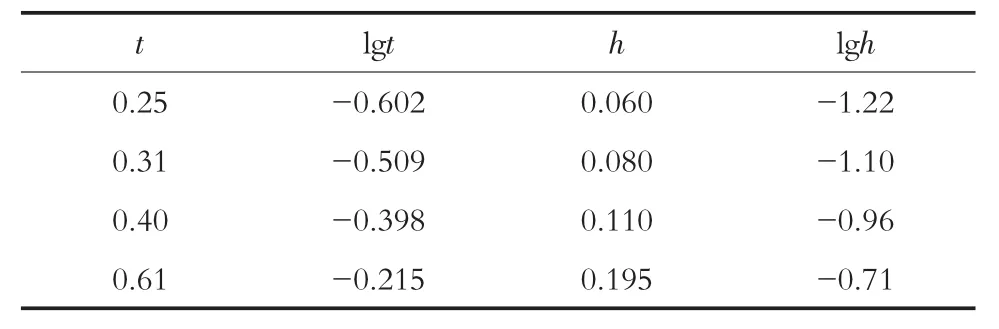
表2 实验数据对数值

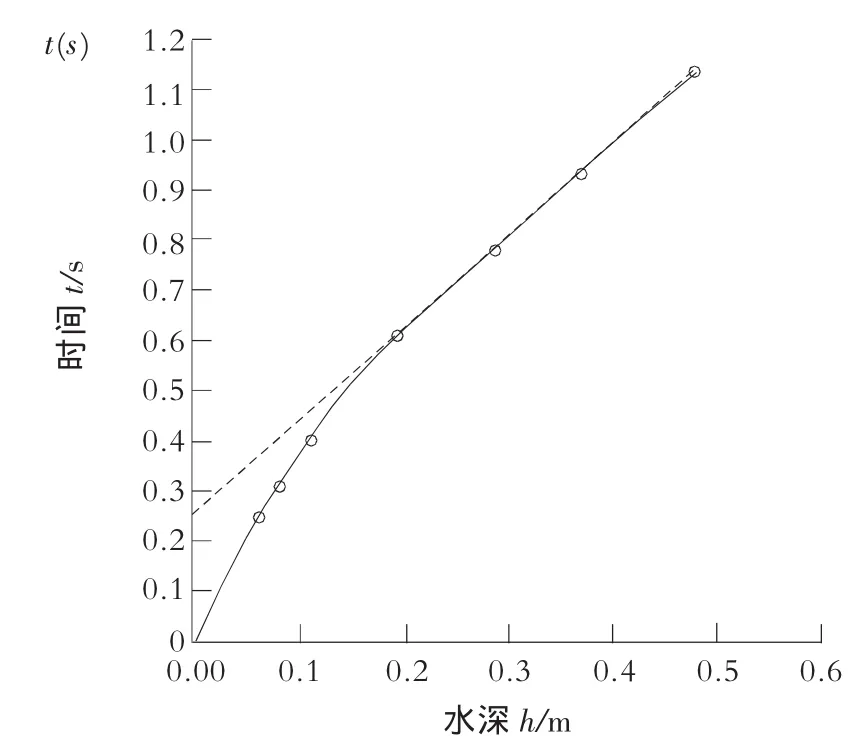
图2 h—t关系图

以lgt为纵坐标，lgh为横坐标点绘关系图，见图3。由关系图发现为直线完全符合幂函数形式。

由计算机拟合出直线方程为：

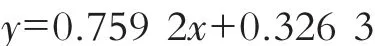
即：

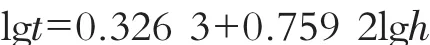
对照lgt=lga+blgh可得：

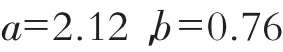
所以气泡上升的幂函数形式为：

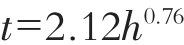
对于气泡上升的匀速段，在h～t关系图上取两点：（0，0.26）和（0.45，1.07）代入直线方程 y=kx+c可得k=1.80，c=0.26，所以直线方程为 t=1.80h+0.26。在实验水深范围内，气泡上升规律为：

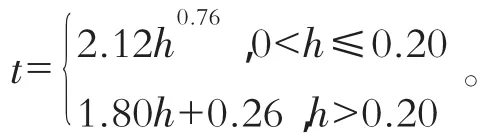
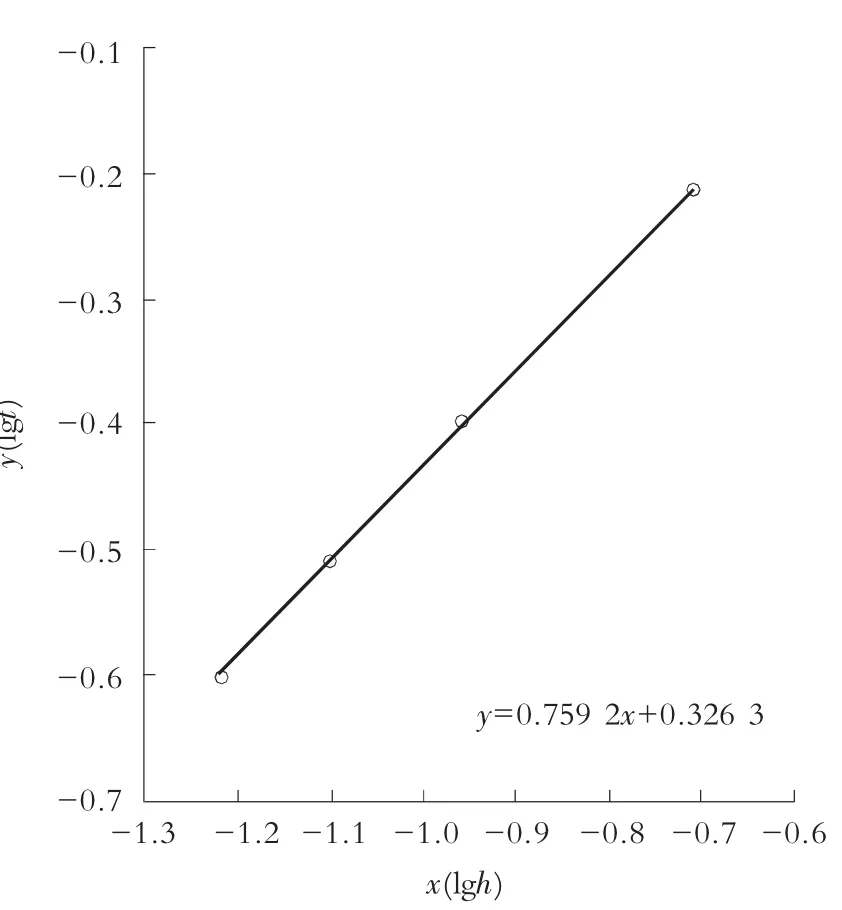
图3 lgt—lgh关系图

确定了气泡上升规律后，它的重要应用就是已知水深，便可计算出气泡的运行时间。当在运动的水流中，已知水深、气泡运行的水平距离便可计算出流速，从而达到在水文测验中测取小水深、低流速的目的。