一种图像置乱的改进算法

何创毅，陈乐庚，王志达

(桂林电子科技大学 计算机与控制学院，广西 桂林 541004)

数字图像作为信息的一种载体，其安全性和其他信息载体一样不容忽视。在传统的密码研究领域里，数字图像并没有作为一种特殊的明文形式而开辟一种特定的加密方式。此外，数字图像所具有的信息量大、数据呈二维矩阵分布、数据冗余量大等特点，使得传统的加密方法对图像并不是十分适应。

基于混沌的图像置乱技术是近年来才发展起来的一种加密技术，它利用了混沌系统优良的密码学特性。由邓绍江等人提出的一种基于混沌的图像置乱算法[1]是通过混沌序列值构造对换规则矩阵，由该矩阵控制二维图像的像素进行对换置乱；陈珂等人提出了一种基于Rijndael的加密算法[2]，改进了 Rijndael中的行、列置换和密钥编排方案，使之成为替代和置换相结合的图像算法；而Gilani等人则提出了一种基于块的增强型的置乱算法[3]，通过对图像的分块，再对块进行两轮的翻转，从而实现图像的置乱。本文提出了一种改进的结合像素位置置乱和灰度值变换的的图像置乱算法。实验表明，该算法具有优良的特性。

1 算法的改进与设计

1.1 混沌映射Logistic

Logistic映射来源于著名的统计学模型，是目前被广泛应用的一种混沌动力系统，其动态的数学模型可表示为：

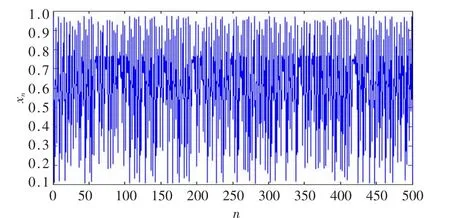
图1 参数 λ=3.889、初值 x0=0.485时的 Logistic映射序列分布

式中，xn为系统变量，λ 为系统参数，xn∈(0，1)，n∈N。 当3.569 945＜λ≤4时，映射式(1)处于混沌状态，式(1)迭代得到在(0，1)上的伪随机序列{xk}。图 1 是在映射参数λ=3.889、初值 x0=0.485时，式(1)所产生的 500个伪随机序列数在区间(0，1)的分布图。图中，x轴表示 n，y轴表示xn。

1.2 密钥的生成

混沌动力系统参数的确定对于算法的安全性具有重要意义。传统算法中采用混沌原理进行置乱加密，其方法是给混沌系统选定一个不变的参数和初始值(用作密钥)，密钥的产生独立于像素值，这导致算法的明文敏感性偏弱，不能有效地抵抗明文攻击和差分攻击。本文提出的算法有效改进了这一缺点。

首先，通过式(2)将原图像像素值的总和映射到区间[0，1]上的一个值，这个值可作为混沌动力系统的初始值k，再通过式(2)和式(3)确定混沌动力系统的参数 u。把混沌映射Logistic式(1)的参数与明文各像素联系起来，有助于提高密钥对明文的敏感性，增强算法抵御明文攻击的能力。

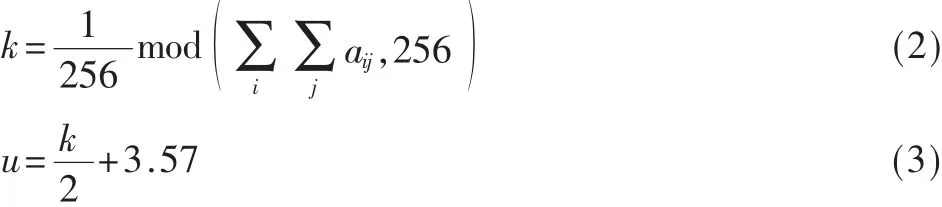
算法是对k值敏感的，像素值的改变将导致k值的改变，从而影响混沌序列值产生的初始条件。所以，通过上述过程，算法的抵御明文攻击的能力得到加强。

1.3 数字图像抽样

从抽样理论，数字图像是二维连续曲面上按照某一间隔和某种策略进行抽样所得的一个二维离散点阵。抽样过程可具体描述如下[4]：

原始图像用矩阵T表示，大小为N×N:

(1)N=2n时，把矩阵T中的奇数列抽出来排成矩阵T1，把偶数列抽出来排成矩阵T2，再把矩阵T1和T2组合成T3，即 T3=[T1T2]，则T3为T的一次列抽样结果。假设矩阵 T的列号为{1，2，3，…，N}，则经过上述的列抽样后按一定的顺序组合，T3可以表示为{1，3，5，7，…，2n-1，2，4，6，…，2n}；然后按行抽样方法对 T3 进行操作，则得到了T′。T′就是T经过一次列行抽样过程所得到的最终结果。

(2)N=2n+1时，除最后一列，最后一行不变外，其抽样过程同N=2n时一样。

如图2所示的3×3矩阵的抽样过程也可以用矩阵表示为 T′=XTY，其中T为原始图，X和Y分别为列和行的抽样矩阵。

图2 3×3矩阵按列、行抽样过程

与其他一些用混沌映射实现图像像素置乱的方法相比，该方法具有算法简单、执行速度快等特点。因此，可作为图像加密的一种预处理方法。

1.4 灰度值变换

置乱和变换是图像加密技术中两个基本方法。下面将介绍对像素灰度的变换处理。设I(i，j)为位置为(i，j)的 像 素 的 灰 度 值 ，I′(i，j)为 I(i，j)经 过 替 代 变 换 后 的 值 ，I′(i′，j′)为 替 代 操 作 循 环 中 ， 上 一 个 处 理 过 的 像 素 灰 度值。 利用 Logistic 映射式(1)，其密钥 key1={μ1，x1，m}。 其中，μ1由式(2)和式(3)联合产生的 μ变化而来；而 x1为混沌映射的初始值，由算法指定；m则表示取迭代m次(可设m＞10 000)之后的混沌序列产生的{an}。由于混沌映射初始产生的伪随机序列取值范围在(0，1)，不适合直接应用在灰度值的变换过程中。为此，通过式(4)对伪随机序列{an}放大，产生新的伪随机序列 Cn。即：

式中，round函数表示四舍五入取整。则图像像素的灰度值变换可表示为：

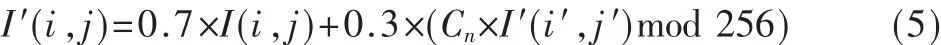
由式(5)可以看出，灰度值的变换过程将加密图像中每一个像素值都联系在一起，也就是扩散到如密图像的所有像素中，因此改变任何一个像素的像素值，都会影响所有像素的像素值，从而提高了算法的安全性。

1.5 块的全局置乱

传统的图像局部置乱是将一幅图像分成几块，然后分别对不同的块施加不同的加密次数，从而达到图像的局部置乱。这种方法不足之处：像素的扩散范围只是局限在图像的分块，置乱的程度不够彻底，有可能从密文图像的轮廓中得到原图的部分信息。块的全局置乱和灰度值变换两种方式的结合有效地提高了图像加密算法的安全性，增强了图像的加密效果。在此基础上，把密文图像按一定大小的比例进行分块，并以块为单位进行全局置乱变换。图3说明了一个图像的4个子块利用伪随机序列{a1，a2，a3，a4}的置乱过程。

图3 图像块置乱过程

对一幅 256×256的图像采用 8×8的块进行分块，共分得1 024块，并对每个块用数字1～1 024进行标记。利用 Logistic 混沌映射，取密钥为 key2={μ2，x2}，其中 μ2为式(2)和式(3)联合产生的变化而来，而 x2为混沌映射的初始值，由算法指定。所产生的伪随机数列 {an}，n=1，2，…，1 024，并存储在数组 X中，建立数组下标与块标记的对应关系。通过对数组X排序，即可对各个分块进行重新组合，达到块置乱的目的。这样做的好处是在保留了全局置乱变换优势的同时，还降低了计算强度和空间需求，而且运算的速度非常快。

2 算法描述与仿真

2.1 算法描述

设对大小为N×N、灰度级为256的图像 T进行置乱加密。算法的具体步骤如下：

(1)利用式(2)和式(3)计算图像 T中的所有像素值，生成密钥K。

(2)将密钥 K代入Logistic混沌映射公式中，生成m次迭代以及块置乱所需的混沌伪随机序列。

(3)读入原始图像T的矩阵数据，利用抽样技术对矩阵进行抽样，实现矩阵行、列的交叉置乱。可进行多次迭代，最后所得图像为T1。

(4)对置乱后的图像T1，按行从上到下、从左到右的顺序依次扫描，应用式(5)对图像像素灰度值进行变换。

(5)重复步骤(4)和(5)，直到图像T1中的所有像素值都被变换，所得图像为T2。

(6)对T2进行分块，把分块与置乱序列对应起来，通过对序列的排序达到分块排序的目的，所得图像为T3。

(7)T3就是原图像T完成一轮置乱加密过程的密文图像。可根据需要进行多次加密。

解密算法是加密算法逆过程，在这里不作介绍。

2.2 算法仿真

该算法采用MATLAB平台进行实验仿真，采用模块设计的方法实现加密算法和解密算法。在实验过程中，用于图像置乱的灰度图像大小256×256。用本文所提出的算法对图像进行置乱加密，所得到的图像均是一种类似于噪声的均匀图像，且完全不能从图像中得到原图的任何信息，具有良好的加密效果，如图4所示。

图4 图像置乱加密前后对比

3 算法安全性分析

3.1 密钥空间分析

基于混沌映射的加密算法，参数(包括初始值)往往用作密钥，控制参数多就意味着密钥也多，因此参数空间大才能保证密钥空间也大。假设一个算法有a、b、c、d 4个控制参数，那么攻击者必须猜对这4个参数的排列组合才可能破译算法。如果这4个参数是从1～64的任意数，则密钥空间大约为644。本文提出的算法中，算法的密钥由产生灰度值变换伪随机序列的key1和产生块局部置乱的伪随机序列的key2两部分组成，则整个加密系统的密钥为：

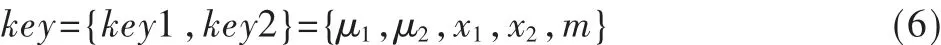
从式(6)中可以看出，最终的密钥参数有5个，而且每个参数都有着非常大的取值范围，因此算法有足够大的密钥空间，使得穷举攻击不可能。在这样的一个密钥空间中，采用穷举法进行攻击，在一些实时性要求较高的保密通信系统中，即使找到了加密密钥，由于其滞后的时间太多，已经失去了攻击的价值。

3.2 直方图分析

对比图 5(a)和图5(b)可以明显地发现，明文图像的各灰度值的像素个数分布从0～1 500不等，其中的差别非常大；而在密文图像中，像素个数则主要分布在[225，275]这个区间里。其分布均匀的特性表明，该算法具有良好的置乱特性，能有效地掩盖明文图像的像素分布规律，有效增强图像安全性。

图5 直方图

本文介绍的算法在对图像运用数字图像抽样技术预处理的基础上，利用Logistic映射产生的伪随机序列，对图像进行灰度值的变换和全局的块置乱。实验仿真表明，该加密算法具有良好的加密效果，能有效地抵抗统计攻击和抵御差分攻击；算法具有足够大的密钥空间，能有效地抵抗密钥穷举攻击。

[1]邓绍江，张岱固，濮忠良.一种基于混沌的图像置乱算法[J].计算机科学，2008，35(8):238-240.

[2]陈珂，崔志明.改进的加密算法在医学图像上的应用[J].计算机工程与设计，2009，30(3):752-754.

[3]GILANI S A N，BANGASH M A.Enhanced block based color image encryption technique with confusion[C].Multitopic Conference，2008.

[4]熊昌镇，邹建成.数字图像抽样技术的置乱效果及分析[J].北方工业大学学报，2002，14(3):5-12.