求解一类随机优化问题的社会认知算法
2010-08-08万东
万 东
(广东交通职业技术学院,广东 广州 510650)
随机优化问题通常因为缺少结构信息而存在不确定因素,并且优化目标的精确解析表达式很难得到,固难于高效实现全局优化。另外,优化决策空间很大,且往往是连续量和离散量、逻辑量并存,优化涉及多个目标,并存在多个极小点,这更增大了此类问题的优化难度。因此,对随机优化问题的研究已成为国际学术界的一个重要研究课题[1-3],许多学者都在寻找一种高效、鲁棒的优化算法。
近年来,出现了几种智能优化算法,如模拟退火算法、遗传算法、免疫算法、演化算法、粒子群算法等。但这些算法绝大多数是针对确定性优化问题的。社会认知算法SCO(Social Cognitive Optimization)是一种群体智能算法[4-5],是基于社会认知理论的集群智能优化算法,它对目标函数的解析性质没有要求,适合于大规模的约束问题的处理,该算法已经表现出了良好的效果[6-7]。本文结合社会认知算法,提出了解随机优化问题的社会认知算法。该算法易理解,并易于程序实现,是一种高效的、鲁棒的优化算法。这不仅为随机优化问题的求解提供了一种新的途径,还为社会认知算法的应用拓展了新的空间。数值仿真结果表明了该方法的有效性。
1 社会认知优化算法概述
社会认知优化是基于社会认知理论(Society Cognitive Theory)发展起来的一种智能优化算法。社会认知理论认为:人格是综合遗传、环境和认知而形成的,特别重视环境和认知的作用,强调人际之间社会学习的重要性。社会认知优化是通过竞争选择和领域搜索来模拟社会认知理论中的社会学习能力,用代理代表社会中的人,用知识库代表社会中的知识,通过代理与知识库之间不断的交互来模拟人类的社会学习过程,从而达到优化学习的目的。
1.1 社会认知算法的相关概念
知识点(Knowledge point):知识点是位于搜索空间中对位置及其适应度水平的描述所构成的点。
库(Library):库是含有一系列知识点且具有大小的表。
学习代理(Learning agent):学习代理是一个行为个体,支配库中的知识点。

整个优化过程如图1所示。
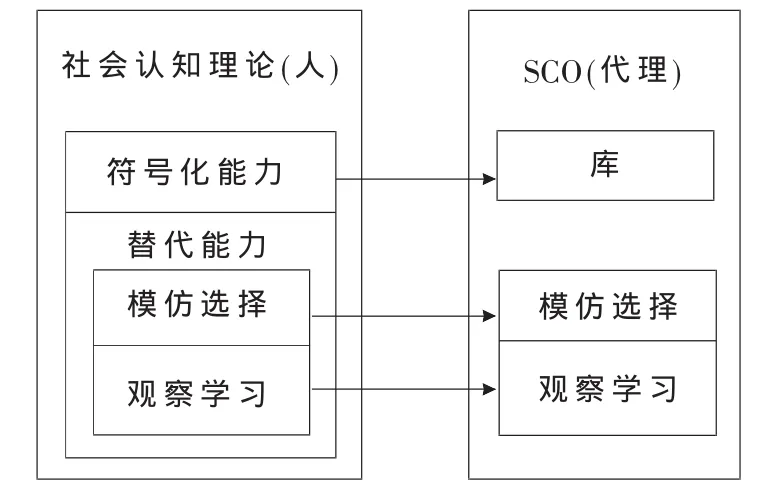
图1 社会认知优化原理图
1.2 社会认知优化算法的实现过程
假设库中知识点为Npop,学习代理的数量是Nc,一般选择Npop=3Nc。实现过程步骤如下:
(1)初始化过程
①随机生成Npop个知识点;
②给每个学习代理分别随机分配库中不同的知识点。
(2)替代学习过程
①模仿学习:在库中随机选择2个不同的知识点,采用竞争的原则在两者中选出一个好的知识点;
②观察学习:把选择出来的知识点和代理自身的知识点进行对比,取水平较好的点作为中心点,取较差的点作为参考点,基于领域搜索的原则将这两个点移动到一个新的知识点,储存新的知识点。
(3)从库中去掉1个最差水平的知识点。
(4)重复步骤(2)~(4),直到满足停止条件。
2 数值仿真结果
本文采用非凸二维随机Rosenbrock函数和多极小的随机Goldstein-Price函数进行仿真研究。文中参数选取如下:Npop=350,Nc=70,T=1 000。最大截止代数见表 1,精度为1×10-6。对下述问题进行 50次计算,用 VC++6.0编程,计算结果见表1。
(1)随机 Rosenbrock函数
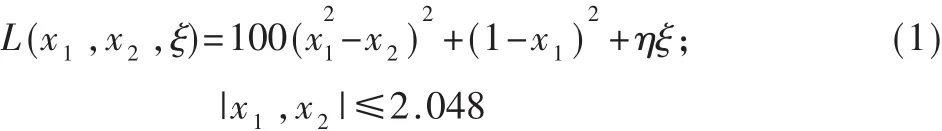
其中:η为噪声幅度,取为 0.01和0.05;ξ为随机噪声,在此令其服从[0,1]的均匀分布。 显然 E[L(x1,x2,ξ)]的最优解为(1,1),其最优值为 0。
(2)随机 Goldstein-Price函数
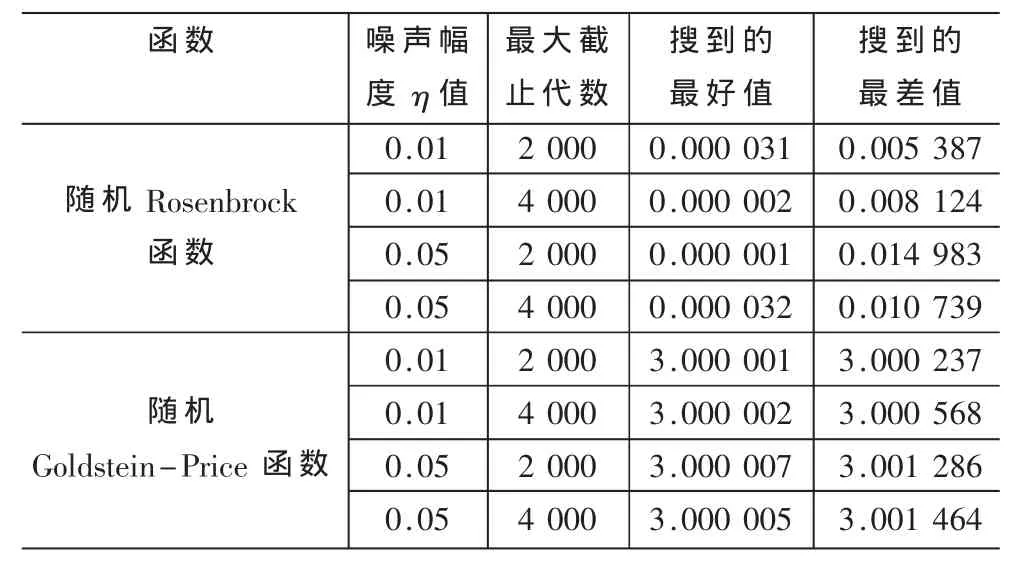
表1 随机优化问题的社会认知算法数值结果

其中:η为噪声幅度,取为 0.01和0.05;ξ为随机噪声,在此令其服从[0,1]的均匀分布。显然 E[L(x1,x2,ξ)]的最优值为3。
基于以上仿真结果,本文可得如下结论:(1)社会认知算法求解随机优化问题具有良好的鲁棒性。最大截止代数增大时,随机仿真结果与理论上的最优解较接近。(2)当噪声幅度较大时,相同参数下的随机仿真结果变得较差。
本文把社会认知算法应用于求解随机优化问题,并通过数值仿真进行了验证。结果表明,社会认知算法具有有效性和鲁棒性,在求解随机优化问题方面具有很强的优势和应用价值。文中用到的随机噪声为均匀分布,但现实中遇到的噪声复杂得多,所以社会认知算法应用于求解随机优化问题还有待进一步研究。研究方向包括:通过把社会认知算法和其他技巧相结合来进一步提高算法的效率和精度;进一步研究高效的适合高维随机优化问题的群体智能算法;针对随机组合优化问题推广研究此类算法,进一步拓广其应用领域。
[1]王凌,张亮,郑大钟.仿真优化研究进展[J].控制与决策,2003,18(3):257-262.
[2]王凌,郑大钟.随机优化问题的一类基于假设检验的模拟退火算法[J].控制与决策,2004,19(2):183-186.
[3]张亮,王凌,郑大钟.随机优化问题基于假设检验的遗传算法[J].控制理论与应用,2004,21(6):883-889.
[4]XIE X F, ZHANG W J, YANG Z L.Social cognitive optimization fornonlinearprogramming problems[C].Beijing,China:Int Confon Machine Learning and Cybernetics,2002:779-783.
[5]XIE X F,ZHANG W J.Solving engineering design prob-lems by social cognitive optimization[J].Genetic and Evolutionary Computation Conference,2004:261-262.
[6]苏俊霞.社会认识优化在非线性规划问题中的应用[J].计算机仿真,2007,24(9):261-264.
[7]张建科,孙家泽,寇晓丽.求解分式规划的社会认知算法[J].计算机工程与设计,2008,29(21):5543-5545.
