车辆段入线调车算法研究

范新龙，张欣亮，史新伟

（1.西安铁路职业技术学院，西安 710014；2.西安铁路局，西安东车辆段，西安710608）

目前，车辆段自动化入线调车存在许多问题，人工过程很容易理解和实现的问题，用自动化方式则较为复杂，考虑到通用性，决定采取一次一辆的方式进行调车，即根据从图像化界面得到的调车信息及机车所在的位置，每次从所选的股道取一车辆，根据车辆中所含的调车信息，将此车调至相应的股道，如此产生的调车序列不能作为实际的入线计划，须进行优化处理。优化方法在实现时有许多优势：（1）可以有多种组合，便于提取最优组合使用。（2）可以根据调车线的长度合并数据，在调车线较短的车辆段使用尤能体现其优点。在实际使用中，可根据车辆源（源）、维修台位（目的）或两者结合使用相应的算法，本文主要研究车辆源调车算法。

1 两个概念

1.1 定位调车

所谓定位调车，就是指定待修车辆调入指定的待修台位，对某些有特殊需要的车辆进行这类调车操作，在图形化调车系统中，定位调车通过直接拖动待修车辆到维修台位上得到调车信息。

1.2 定性调车

定性调车只指示出待修车辆将进行什么样的维修操作（段修、厂修、洗罐等）而不指定具体的维修台位，在图形化调车系统中，通过设定待修车辆的调车性质得到调车信息，在下面的算法中，许多情况是针对这种调车方式进行的。

2 用例

这里的用例指的是车辆源调车过程产生的数据，主要用于说明算法，分基本用例和扩展用例两类。基本用例反映了采用车辆源调车的最原始数据，扩展用例是对基本用例进行部分优化后的结果，主要用于说明算法优化。在下面的分析中，S表示待调的源车辆及股道；D表示目标台位股道及车辆。由于合并算法可以看作是将相邻两次调车信息进行合并，所以用A、C分别表示第N次和第N+1次牵出股道名称，B、D表示第N次和第N+1次的推入股道名称，m、n表示每次牵出或推入的车辆数。

2.1 基本用例

基本用例接近原始调车数据，当m、n为1时（每次牵出和推入的车辆数为1），即为原始数据；如果m、n不为1，则是优化过程中的数据。

……第n钩

上例中，A + m 和B－m 表示从股道A中牵出m辆车辆，推入目的股道B中，C+n和 D－n同上，只是下一钩的操作。当m、n为1时，表示在没有优化情况下的调车过程，即每次从待调股道牵出一辆车并将其推入目标轨道。

2.2 扩展用例

上述过程中，如果不进行优化，则可能造成调车钩数过多，扩展用例则是将基本用例中可以合并的项目进行合并处理，处理后的结果可以减少调车计划中的钩数，这个结果更接近于实际的入线计划。

（A1股道牵出m1辆，A2股道牵出m2辆，……）

（将n1辆推入B1股道，n2辆推入B2股道，……）

这4项中的n可以不相等，即牵出的车辆可能与推入的车辆不等。

基本用例可以看成为扩展用例的特殊形式，本文的优化算法将主要讨论扩展用例的算法，但因为基本用例的特殊性，有些算法在基本用例中会有其特殊点。另外基本用例的引入也便于对本文的理解。

3 优化算法

优化算法主要用于将原始数据进行优化处理，得到比较合理且最优的入线计划，其原则为：

（1）优化后，总钩数比优化前少。

（2）钩数相同的情况下，调车线所需长度短。

原始的牵出和推入的顺序为ABCD，即一次牵出（A）、一次推入（B），再一次牵出（C）和一次推入（D），优化处理后则为先做两次连续牵出（AC或CA）、再作两次推入（BD或DB），注意这种操作有先后顺序的要求。

由于优化过程实际上是根据各种条件，对现有钩数进行合并，所以也称此为“合并律”，根据合并方式，合并律主要有CABD律和ACDB律两种合并方式（CABD和ACDB表示牵出和推入的顺序）。

3.1 CABD律

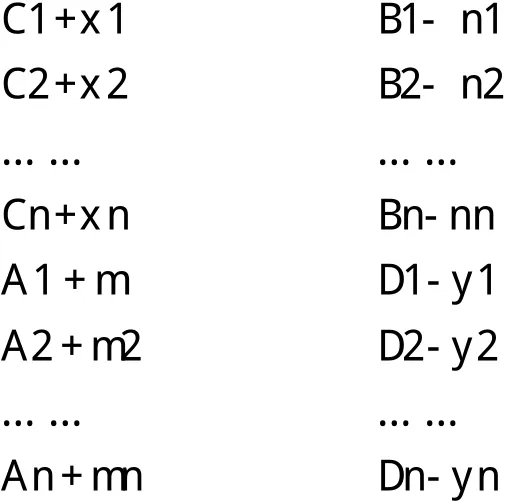
3.2 ACDB律

3.3 优化条件

以上的优化有诸多条件限制，除了台位不同的在合并时要注意台位位置先后外，车位的先后也很重要，上述过程中可以看到对“出”、“入”的顺序有调整，在定位调车时，由于车台位已经指定，合并后必须能够到达指定台位位置，对定性调车而言，要注意的一个很重要的原则就是合并时，“出”位一定要在“入”位前。

通过实践分析总结，上面两种合并律的执行条件如下：

If ((A1=Cn) and (An=C1)) then ；源全同，A、C为牵出

if (B1<>Dn) and (Bn<>D1) then ACDB ；目标全不同 B、D为推入

if (B1=Dn) and (Bn=D1) then ACDB ；目标全同

if (B1=Dn) and (Bn<>D1) then ACDB； 目标前同

if (B1<>Dn) and (Bn=D1) then CABD ；目标后同

end；

if (A1<>Cn) and (An<>C1) then ；源全不同

if (B1<>Dn) and (Bn<>D1) then do nothing；源全不同,目标全不同

if (B1=Dn) and (Bn=D1) then CABD；源全不同，目标全同

if (B1=Dn) and (Bn<>D1) then ACDB ；源全不同，目标前同

if (B1<>Dn) and (Bn=D1) then CABD；源全不同,目标后同

end；

if (A1=Cn) and (An<>C1) then；源前同

if (B1<>Dn) and (Bn<>D1) then CABD；源前同，目标全不同

if (B1=Dn) and (Bn=D1) then CABD；源前同，目标全同

if (B1=Dn) and (Bn<>D1) then do nothing；源前同，目标前同

if (B1<>Dn)and (Bn=D1) then CABD；源前同，目标后同

end；

if (A1<>Cn) and (An=C1) then；源后同

if (B1<>Dn) and (Bn<>D1) then ACDB；源后同，目标全不同

if (B1=Dn) and (Bn=D1) then ACDB；源后同，目标全同

if (B1=Dn) and (Bn<>D1) then ACDB；源后同，目标前同

if (B1<>Dn) and (Bn=D1) then do nothing；源后同，目标后同

end；

3.4 特殊情况

当N和N+1调车数量均为1时（基本用例情况，m、n都为1），根据基本用例对上述算法优化：

当A = C并且B = D，两次牵出股道号相同、推入股道号相同。

S：A+(m+n)

D：B-(m+n))

当A=C 并且 B<>D (ACDB律)

S: A+(m+n)

D: D-n

B-m

当A<>C 并且 B=D （CABD律）

S: C+n

D: A+m

B-(m+n)

4 结束语

调车源分析算法可以解决部分车辆段入线计划自动生成问题。为了得到最优的调车方案，该法利用了轨道的全排列，当待调车辆来自多个轨道时，其运算次数达到N！（N为待调车辆轨道数），通过对这些比较，得到最佳的源股道排列顺序。由于该法所需时间较长，有些情况下还不能得到最优方案，又进行了目标算法分析，这种算法将在“车辆段入线调车目的台位分析算法研究”予以介绍。这两种算法的联合使用，能解决大部分的自动生成入线调车计划中存在的问题。

[1] 胡思继. 铁路行车组织[M] . 北京：中国铁道出版社，2002.

[2] 步文亮，王洪昆，刘光涛. 车辆段调车作业全过程自动化的研究与实现[J] . 铁道机车车辆，2007（6）.

[3] 冯俊杰. 铁路运输基本技能训练[M] . 北京：中国铁道出版社，2003.

[4] 西安铁路局西安东车辆段调度科文件.厂段修车辆入库前预检及调车作业规定[S] . 2008，7.

[5] 西安铁路局西安东车辆段调度科文件. 段内各线路存车数量及规定[S] . 2009，7.