基于MIMO系统的球形译码算法的改进

陈云杰， 吴耀军， 居贝思

（华东理工大学 信息学院，上海 200237）

0 引言

MIMO(多输入多输出)系统是近十年来现代数字通信领域最重大的技术突破之一。其优势在于潜在容量巨大，且随着收发天线数目较小的一方呈线性增长。但是 MIMO系统在带来巨大容量的同时，也产生了极大的接收信号检测复杂度。球形译码（SD）算法[1]最早由Fincke和Pohst提出，用于研究整数最小二乘问题。Viterbo和Biglieri将SD算法引入到通信领域的多维星座的最大似然检测中。已经证明，采用穷尽搜索的ML检测算法的复杂度随天线数呈指数增长，而 SD算法的复杂度在很大信噪比范围内与天线数呈多项式关系。因此，球形译码 SD算法可以用较少的计算量来获得最大似然译码性能。但是也存在着一定的不足，如初始半径的选择，更新半径的选择和迭代次数等等。

在本文中，提出一种新的改进的球形译码算法，它比传统的算法要快得多。在文中，通过改变半径收缩的速度来减小译码的复杂度。

1 MIMO 系统模型

考虑一个Nr×NtMIMO系统[2]，该系统有Nr个接收天线和Nt个发射天线。在该系统中，信道为平坦衰落信道，接收信号可以被表示为：

2 球形解码及其改进

2.1 传统的球形译码算法[3]

球形译码的基本思想是在以一个矢量为中心的半径为 d的多维球内搜索格点通过限制或者减少搜索半径从而减少搜索的点数，进而使得计算时间减少。

复数表示的矩阵等式(1)能被转换成实数的矩阵，其维数为原矩阵的两倍，如下所示：

在球形译码中，球中的格点应该能满足下面的不等式：

为了解决这个问题，我们可以对矩阵H进行QR分解[4]：

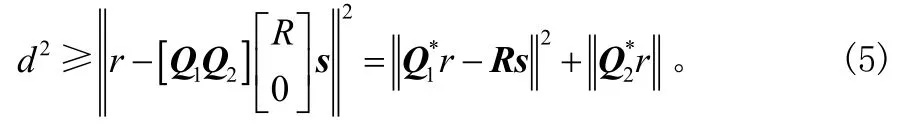
式（5）中( )*表示赫米特矩阵转置，式(5)可以表示为：

式中,ijr 表示矩阵R中的第(i,j)个元素。R是上三角矩阵，根据上三角矩阵的性质，我们可以得到上不等式的右边(RHS)能被展开成下式：

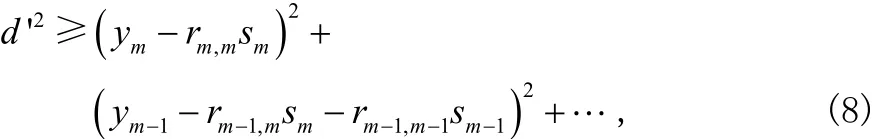
式中,右边第一项决定于sm,第二项由来决定,以此类推。因此，一个在球内的点需满足条件这个条件等价与sm属于下式表示的范围：

当然，对于每一个sm也要满足式(7),这里定义

式（6）中的前两项是一个更需要满足的条件，其使sm-1属于下式表示的范围：

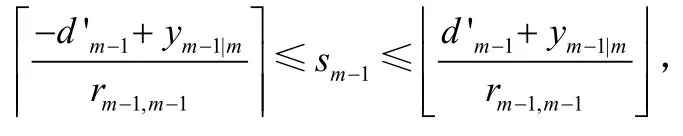
以此类推，可以用这种形式表示出sm-2，一直到s1。因此，我们可以满足式(3)的所有网格点。

2.2 改进的球形译码算法

在前面的部分中已经提到过，传统球形译码的一个重要因素是搜索半径d的初始值。在这个部分中，我们提出一种改进的球形译码算法，它的初始半径d的选择变得并不重要。在这个算法中，首先，我们选择d为一个很大的值（如+∞），接着在传统的译码算法上进行改进，以弥补这个半径的选择，并减少该算法的复杂度。

在我们改进的方法中，我们主要的思想是加快半径的缩减速度。在改进的算法中，无论何时一个点在球内被找到，新的半径被定义为，在式中d'2前一个被发现点到球心距离的平方。其中，参数度量参数k(0≤1≤k)加快球形半径的缩减速度。首先，初始半径d应该选择的一个很大的值（如+∞）。换句话来说，在第一阶段，搜索区域是没有限制的。但是，当第一个点被找到后，搜索半径将被设置成该点到球心的距离的平方。其中，系数k(t)被定义如下：

式中，t是在第n维网格中点的数目,α,β是控制收缩性能的参数，要进行合适的选择。

参数α和β用来控制弯曲部分的斜率和位置。对于α=∞的情况，参数k的值是1，在这种情况下，其性能等价于传统的球形译码算法。从∞开始递减α可以加快算法的运行速度。通过减小α，我们可以提高算法的速度。但是，对参数α或β取一个很小的值可能会产生一些错误，且使其译码的性能有所下降。我们可以通过t的最大值来选择参数α和β。t的最大值是由信号选择的星座图来决定的。如在4-PSK调制系统中的最大值是4([1+j,1-j,-1+j,-1-j])。

3 仿真结果

在仿真(如图 1，下页图 2所示)中，我们采用两个发射天线和两个接收天线的MIMO系统。信息符号是从QPSK 星座图中选取的。信道转移矩阵H是随机独立高斯的，方差是0.5。在最初译码时，我们选取d的值等价于∞。接着，我们可以比较最大后验概率译码（MAP）、改进的球形译码算法和传统的球形译码算法。

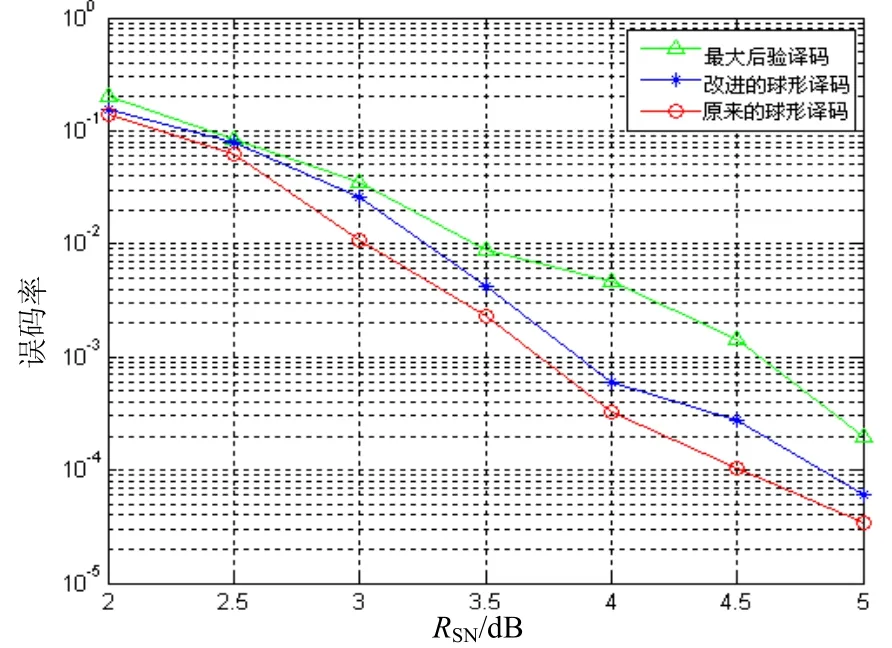
图1 α=5,β=3时的误码率

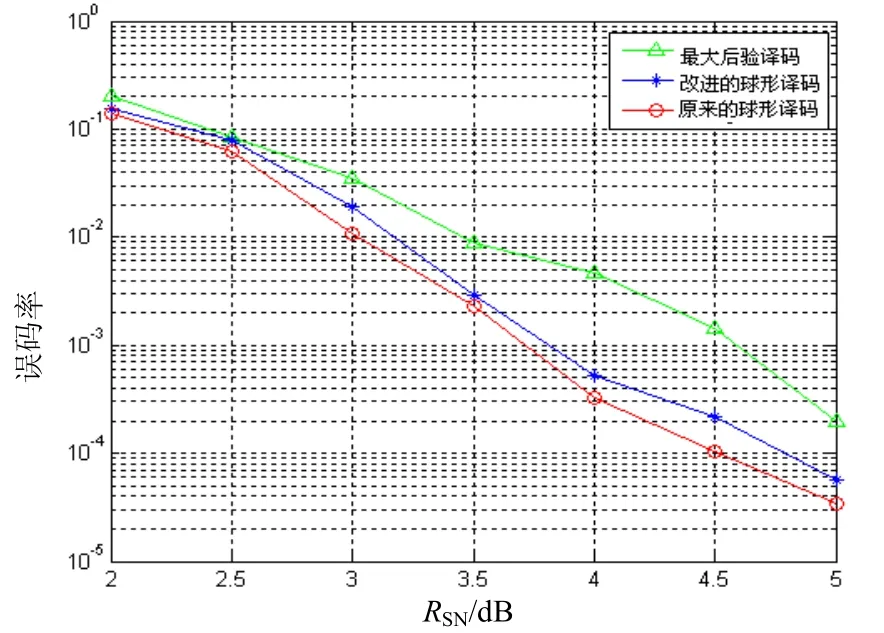
图2 α=β=8时的误码率

图1,图2表示在锐利衰落信道中，参数α和β在不同的取值情况下，最大后验概率译码（MAP）、改进的球形译码算法和传统的算法的误码率。从图1，图2中可以看出，随着信噪比的增加，在相同的信噪比情况下，在误比特率上，改进的球形译码算法在性能上非常接近于原来的算法，但其译码的速度提高了，随着α和β的取值变小时，其译码性能有所下降，但误码率要比没有进行球形译码检测的MAP译码小的多。

4 结语

在本文中，我们提出在MIMO系统中应用的一种新的快速球形译码算法。在改进的译码算法中，与传统的译码算法相比，我们加快了搜索半径的减小速率。因此，改进算法的译码速度比传统的译码速度更快。

我们也利用 Matlab软件进行仿真，展示了最大后验概率译码（MAP）、改进的球形算法和传统的球形算法的比较。在改进的算法中，第一阶段不限制搜索的区域。因此，初始半径的选择变得不重要。可以看出，改进的译码算法比传统的算法更快，且译码性能也接近于未改进的球形译码[5]。

[1] Hochwald B M,Brink S T.Achieving Near-Capacity on a MultipleAntenna Channel[J].IEEE Transaction on Communication,2003,51(03):389-399.

[2] Burg A, Borgmann M, Zellwegger M. VLSI Implementation of MIMO Detection Using the Sphere Decoding Algorithm[J].IEEE J.Solid-State Circuits,2005,40(07):1566-1577.

[3] Hassibi B, Vikalo H.On the Sphere-Decoding Algorithm I.Expected Complexity[J].IEEE Transaction on Signal Processing,2005,53(08):2806-2818.

[4] Razavizadeh M, Vakili T. A New Sphere Decoder for MIMO System[J].IEEE Trans. Inform. Theory,2004,50(04):1639-1642.

[5] 单红梅.MIMO系统中一种子空间追踪的盲空时多用户检测方法[J].通信技术,2008,41(08):79-80.