区域供冷系统逐时冷负荷的分析及数值预测

蒋小强 ，龙惟定，李敏

(1. 同济大学 机械工程学院，上海，200092；2. 广东海洋大学 工程学院，广东 湛江，524025；3. 同济大学 中德工程学院，上海，200092)

由于建筑能耗占社会总能耗的30%左右，建筑节能已成为节能减排的重要内容之一，而建筑节能的成败很大程度上取决于建筑物空调能耗是否降低。区域供冷作为一种新型节能制冷技术，能同时为多个建筑物或多个用冷区域提供冷量。冷量在冷冻机房集中生产，可采用容量大、能效高的离心式冷水机组，且多个用冷区域会存在1个同时使用系数，主机装机总容量远低于其他制冷方式的容量；同时，系统对环境的影响能被集中控制和处理，故区域供冷是一种节能环保的绿色技术。然而，区域供冷技术实际应用时间不长，许多问题有待进一步探讨。如何正确选择区域供冷系统的设计负荷、合理选择蓄冷量(多数系统结合了蓄冷技术)、优化大容量主机的运行策略，是区域供冷系统当前急需解决的问题。区域供冷系统的负荷与单区域供冷系统不同，它受建筑物的影响更复杂。系统设计总负荷并非各区域设计负荷的简单叠加，而应考虑到区域、设备和房间的同时使用概率，即要乘以 1个同时使用系数，而该同时使用系数该如何选取，一直未能很好地解决。另外，区域供冷系统的主机一般选用容量大、效率高的离心冷水机组，这些机组在低负荷时，运行效率低。为了合理安排主机群的运行方案，最有效的手段是在预测出下1 d的冷负荷逐时负荷的前提下，结合机组自身部分负荷时的性能，对运行策略进行优化。基于以上问题，有必要对实际运行的负荷进行分析，探讨影响负荷预测值的因素，找出区域系统的冷负荷变化规律。关于冷负荷的设计和变化规律的研究很多，如Vrachopoulos等[1]根据建筑物的特点，对居住建筑和办公室建筑的冷量需求进行分析，得到了负荷计算公式；Aktacir等[2]探讨了室外条件对冷负荷及系统设备选型的影响；Corgnati等[3]采用数值和实测的方法对办公建筑冷负荷进行分析。杨培志等[4]研究了汽车空调系统的运行特性。然而，对于多区域供冷系统，人们用实测数据对冷负荷进行的分析较少。关于逐时冷负荷的预测，主要有参数回归法和神经网络法[5-7]。参数回归法主要在分析影响冷负荷的主要参数的基础上(如室外干球空气温度、太阳辐射强度、湿度等)，得出负荷随参数变化的经验公式。神经网络法是一种高级的插值计算方法，计算结果的精度比参数回归法的精度高，但计算过程较复杂，需借助计算机进行计算。不少科研工作者采用神经网络法对负荷进行预测[8-14]。这些研究均以单建筑或单区域的冷负荷进行预测，而区域供冷系统与常规空调系统有着诸多不同，大多数区域供冷系统是24 h运行，影响负荷变化的因素也更复杂。Masatoshi等[14]采用多层神经网络对区域供冷系统的逐时负荷进行了预测，但没有考虑冷负荷在工作日与周末的区别，而且仅根据前1 d的负荷进行预测，因而误差较大。由于区域供冷系统受区域使用特点的影响，负荷在白天或晚上，工作日或周末都会有明显区别，因此，有必要针对区域供冷的逐时冷负荷预测建立新的模型，根据先进计算技术、天气预报的范围，找到更适合区域供冷系统负荷变化的预测模型，分析预测值的变化规律。为此，本文作者首先对区域供冷系统的冷水机组运行参数进行检测，通过冷冻水供回水温度和冷冻水流量得到系统的逐时负荷并对其变化规律进行分析；然后，采用改进人工神经网络法，在考虑日期和时间段的前提下，对下1 d的逐时负荷进行预测。将负荷预测值与实际值进行比较，得到影响预测值相对误差的影响因素。

1 冷负荷的测量方法与预测模型

1.1 冷负荷的测量方法

1.1.1 系统概况

为了得出区域供冷系统负荷的实际变化规律，以上海地区某小型区域供冷系统为研究模型，对其运行参数进行测量。该系统供冷区域总面积约30万m2，主要有商务办公、酒店、商场、餐厅、会议室等用冷区域。系统设计总冷负荷为24 800 kW。

1.1.2 测量方法与仪器

对所有运行冷水机组的冷冻水供、回水温度进行测量(得到温差)，同时测得冷冻水的流量，然后，根据下列公式，可近似得出总系统逐时冷负荷：

其中：Q为系统逐时冷量，kW；C为水的比热容，kJ/(kg·℃)；M为冷冻水的质量流量，kg/h；ts和tr分别为冷冻水的供、回水温度，℃。

温度测量仪为ATAL厂家生产的TEP-109，测量范围为-50～150 ℃；流量传送器为GE厂家生产的型号为 AT868W 超声波流量传感器；数据记录仪为ATAL厂家生产的型号为ATAL ATM-03记录仪。温度及流量由数据记录仪自动记录并存储，每隔1 min采样1次。测试时间共26 d，分别为：2006-06-24至2006-06-30，2006-07-12 至 2006-07-23，2006-08-07至2006-08-13(上海地区空调能耗主要来自第6～8月)。

1.2 冷负荷的数值预测

1.2.1 人工神经网络

人工神经网络系统是指由大量的、同时也是很简单的处理单元(或称神经元)广泛地互相连接而形成的复杂网络系统，它反映了人脑功能的许多基本特征，如学习、归纳和分类，但它并不是人脑神经网络系统的真实写照，而只是对人脑进行某种简化、抽象和模拟，这也是现实情况所能做到的，是目前神经网络研究的基本出发点。神经元是神经网络中最基本的处理单元。从神经元的特性和功能可知，神经元是1个多输入单输出的信息处理单元，而且它对信息的处理是非线性的。根据神经元的特性和功能，可以把神经元抽象为1个简单的数学模型。神经网络计算模型可分3层，分别是输入层、隐藏层和输出层，如图1所示。

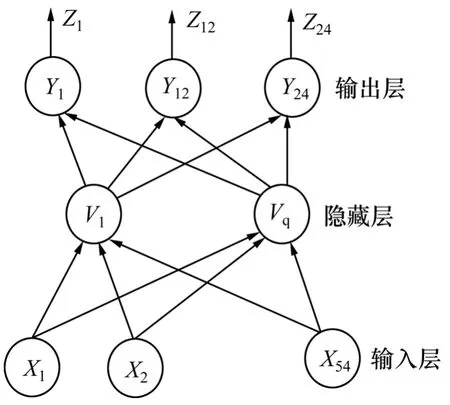
图1 人工神经网络模型(54个输入数据，24个输出数据)Fig.1 Artifical neural network with 54 inputs and 24 outputs

1.2.2 计算模型

应用神经网络法预测负荷，需要知道预测日前一段时间的实际负荷。通过建立区域供冷系统负荷数据库，记录前1周的温度及负荷数据，即

式中：x和t分别表示负荷和温度，下标第1位数分别表示预测日，下标第2位表示预测时刻。

对于输入层中54个输入值，有48个来源于式(1)中实际负荷值，取值规定如下。

若di为星期三、星期四和星期五，则

若di为星期六，则

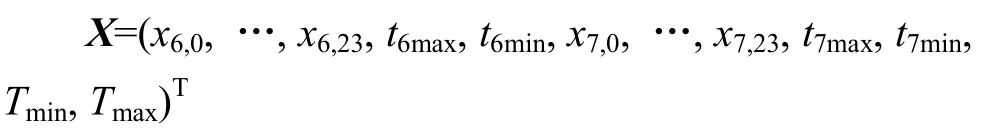
若di为星期日，则

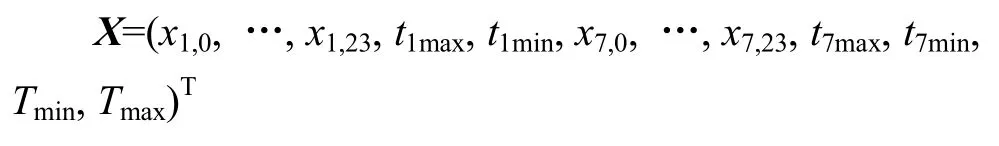
若di为星期一，则

若di为星期二，则

其中：di为负荷预测日；Tmax和Tmin分别为预测日的最高气温和最低气温；X和Y分别表示输入层和输出层，其中，输出层为：

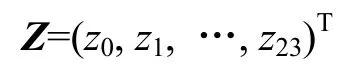
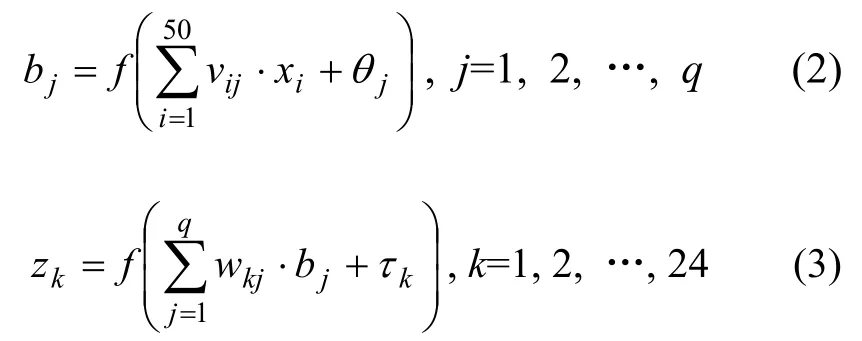
其中：bj为隐藏层第j个输出值；θj为隐藏层第j个阀值；τk为输出层第k个阀值；f(x)为激活函数，，常见的有阶跃型、线性型和“S”型(Sigmoid)3种形式，其中，“S”型函数输出为非线性。考虑负荷变化为非线性，故本文采用“S”型激活函数。

网络权值ωkj和vji由误差反向传播方式来确定。输出值的方差为：

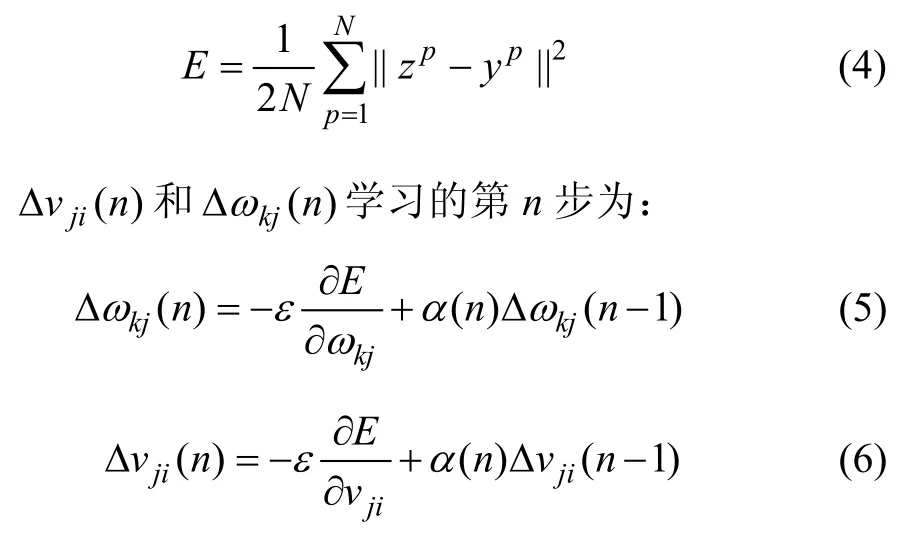
根据网络权值ωkj和vji，系数α(n)的表达式为：

对于非线性系统，

其中：xt为n维的状态向量；yt为P维的测量值；ωt为m维高斯向量；vt为p维的高斯向量；Gt为n×m矩阵；Ht为n×p矩阵。ωt和vt可用式(10)～(12)表示：

其中：Rt和δts为 Kronecker数。假定和，若t≥s，则ft(xt)为n维非线性向量。

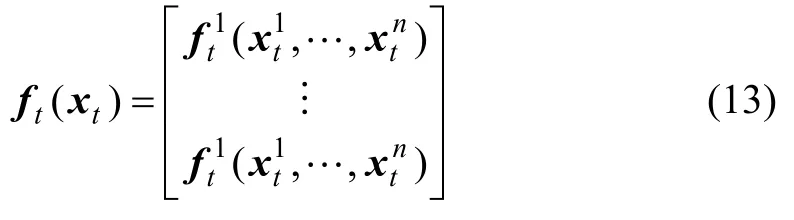
令p=1，vt=ωt=0，则

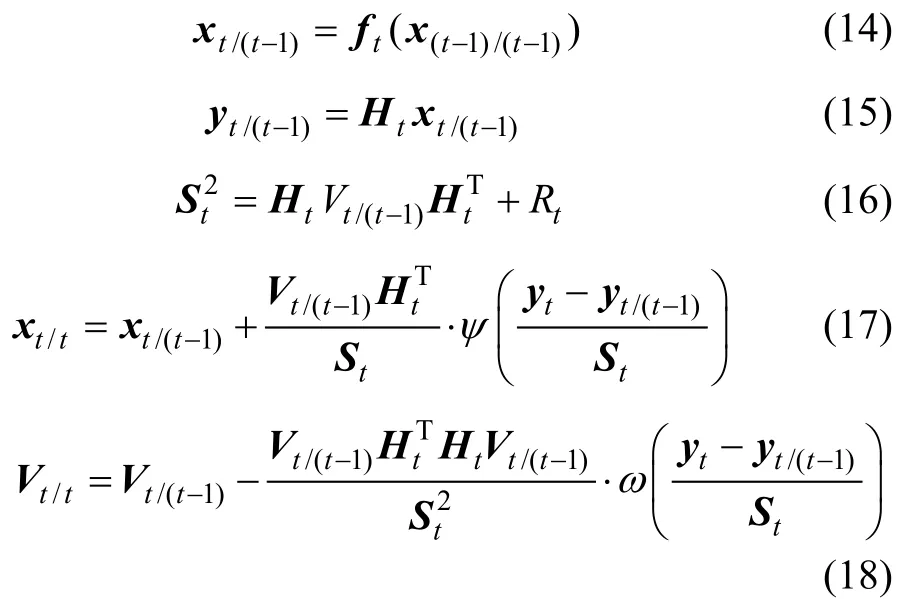
其中：ψ(x)为鲁棒因子；ω为权值。

2 结果与分析

2.1 冷负荷的测量结果

测试期间，2006-07-15，2006-07-16，2006-07-22和 2006-07-23均为周末，全天逐时负荷变化如图 2和图3所示。由图2和图3可见：系统最大负荷在17.0 MW左右，而设计总负荷为24.8 MW，设计负荷超过实际所需负荷45.9%(7月份是上海地区最热月份)。对于工作日全天，上午9:00至下午18:00的负荷较稳定，为15.0～16.5 MW，与约在15:00左右出现的最大负荷相差不大；负荷在18:00之后开始回落，这应该与上海的工作时间有关，上海大部分工作时间是上午9:00至下午 18:00；18:00至 22:00，系统的负荷主要来自商场和酒店，上海的商场一般在22:00结束营业。因此，可以认为：在22:00至次日凌晨的主要冷负荷来自酒店。从图2和图3可以看出：在0:00左右，系统仍有6 MW左右的负荷，说明此时人的活动仍较频繁；随着室外温度的降低以及人的活动减少，负荷约在凌晨4:00左右达最小值2 MW，冷负荷从5:00开始上升，说明一些工作人员如餐饮工作者开始工作了。对于周末，最大负荷出现在上午11:00左右，而非气温最高的15:00左右，这说明，周末的冷负荷更大程度上是由内扰即人流量决定。最大负荷为10 MW左右，仅为工作日最大负荷的58%左右，这与周末上午办公人员休息相关。另外，可以推测出：上海作为国际性大都市，由于交通等客观问题，商场人流量一般在11:00左右达最高峰，较大负荷持续到晚上20:00左右。周末晚上22:00至次日6:00的负荷与工作日晚上负荷相差不大。酒店客人主要可分为出公差和旅游2类，总的来看，酒店无论是周末还是工作日，冷负荷均较稳定。

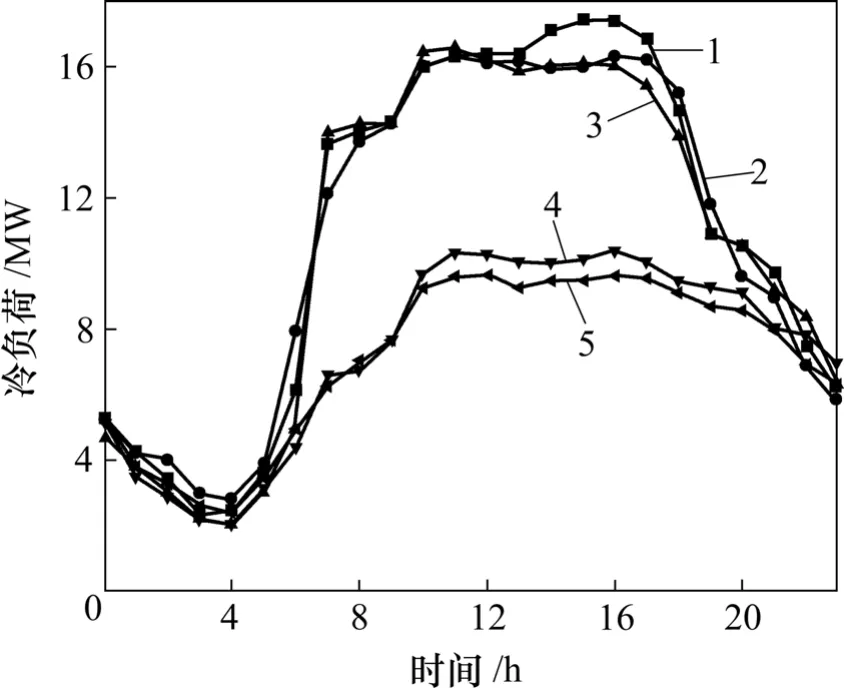
图2 2006-07-12至2006-07-16的实测负荷Fig.2 Actual cooling load from 2006-07-12 to 2006-07-16

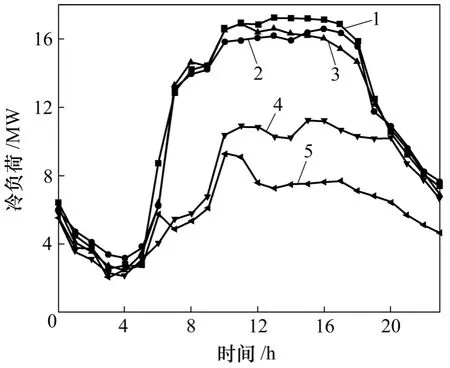
图3 2006-07-19至2006-07-23的实测负荷Fig.3 Actual cooling load from 2006-07-19 to 2006-07-23

测试期间内，逐时冷负荷为设计负荷的 8.1%～68.5%，最小负荷仅为当日最大负荷的11.8%。这说明该系统设计负荷选取过大，系统全天负荷需求变化范围广，对机组运行控制策略要求高。

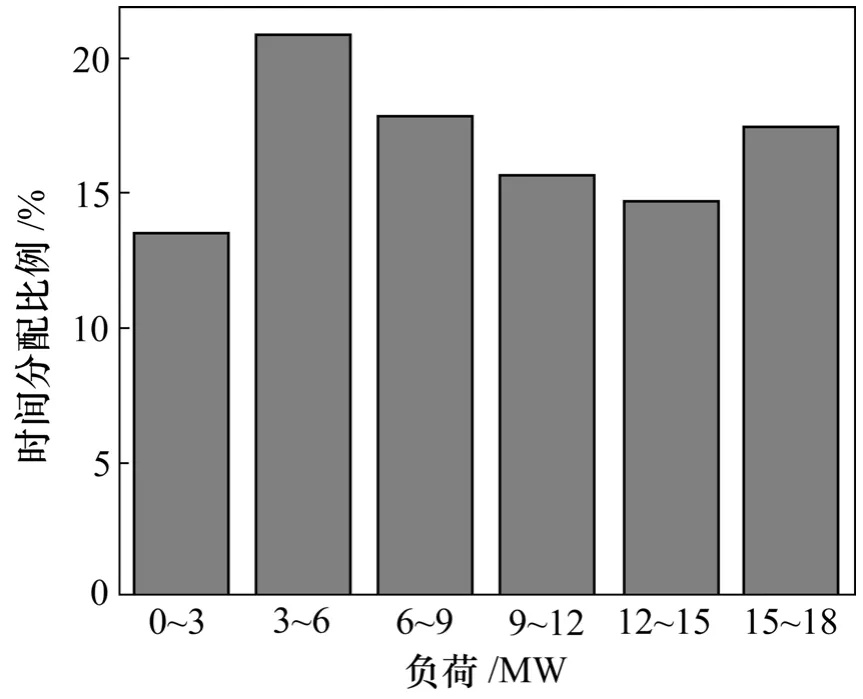
图4 冷负荷运行时间分配比例Fig.4 Proportion of running time under different cooling loads of district cooling system

根据实测结果，该区域供冷系统实际负荷为 0～18 MW，为便于分析，将其均分为6个区间，每个区间相隔 3 MW。图4所示为系统分别在 2006-06-24至2006-06-30，2006-07-17至2006-07-23，2006-08-07至2006-08-13的运行情况，系统在最大负荷区间的运行时间为88 h，所占比例为17%，而在3～6 MW区间的运行时间最长为105 h，在0～3 WM区间的运行时间最短，为68 h。总的来看，系统在各区间的运行时间占运行总时间的比例相差不大。这与单区域供冷系统的负荷变化规律(负荷越大，运行时间越短[15]，负荷越小，运行时间相对较长)完全不同。显然，负荷分布均匀，将有利于机组容量的选配和运行。本系统配备6台制冷量为4 220 kW、2台制冷量为1 400 kW的离心式冷水机组。当冷负荷需求在 15.5～16.5 WM时，主机的运行方式将有一定的局限性，3大主机和2小主机同时工作时供冷量不够，但开4台大主机时供冷量有余；在低负荷如3～4 MW时，开2台小主机时供冷量不够，开1台大主机时冷气存在浪费。考虑离心式冷水机的变容量性能限制，该系统在机组选配方面存在一些不足。建议增加适于变容量调节的螺杆式冷水机组，类似区域供冷系统还可在机组容量选型方面体现一定的梯度。根据负荷需求变化规律，可以为主机容量的选配、运行策略的优化提供理论依据。

2.2 计算值与实测值的比较

2.2.1 工作日的负荷预测

根据数值预测方法，对2006-07-14和2006-07-17这2 d的负荷进行预测。2006-07-14为星期五，因此，它的预测值主要由2006-07-12和2006-07-13实际负荷值来确定；而2006-07-17为周一，根据式(2)，它的预测值由2006-07-13和2006-07-14的实际负荷值确定。逐时冷负荷的预测值和实际值如图5所示，显然，预测值能较好地反映实际负荷的变化规律。

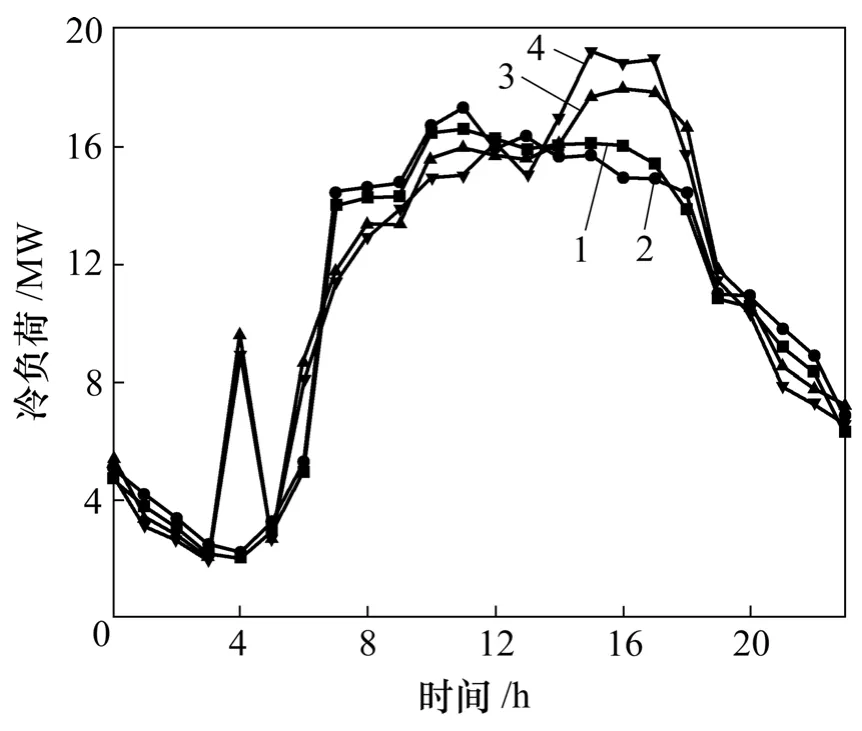
图5 工作日内冷负荷预测值与实际值的比较Fig.5 Comparison of forecast value and actual value of cooling load in weekday

2.2.2 周末的负荷预测

实际逐时冷负荷变化图表明：周末的负荷与工作日的负荷明显不同。因此对周末的负荷预测不能简单对它的前2 d数据进行分析，而应结合上1个周末实际负荷值进行考虑。

图6所示为2006-07-22和2006-07-23负荷预测的结果。2006-07-22为星期六，因此，它的预测值主要由2006-07-15和2006-07-16即上周的星期六、星期日的实际负荷来确定；2006-07-23为星期日，根据式(2)，它的预测值由2006-07-16和2006-07-22的实际负荷确定。同样，从图6可以看出：预测值能较好地反映周末实际负荷的变化规律。

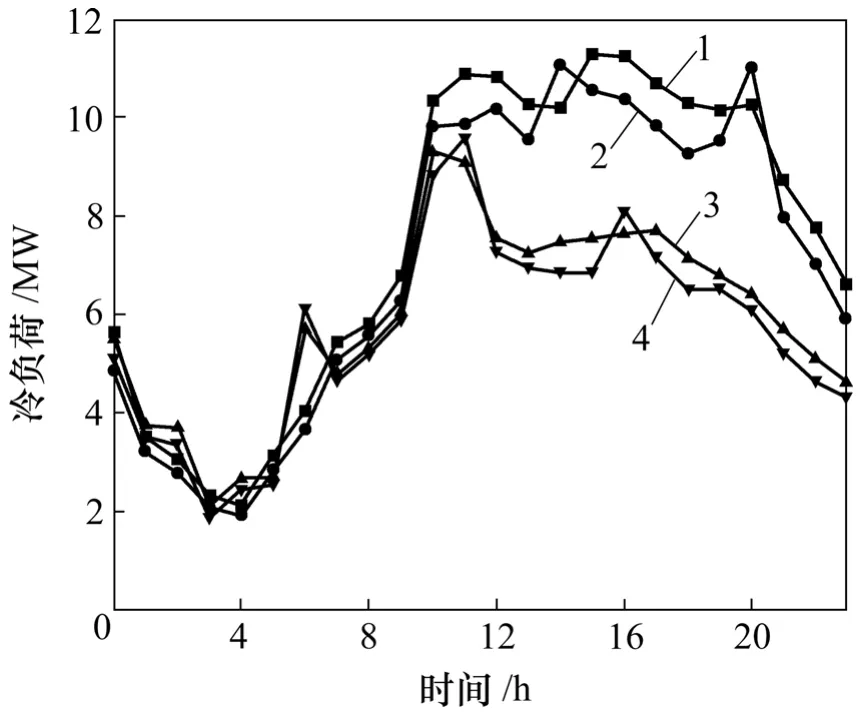
图6 周末冷负荷预测值与实际值的比较Fig.6 Comparison of forecast value and actual value of cooling load in weekend

2.2.3 误差分析

在同一天同一时刻的预测负荷与实际负荷之间距离即为此时刻的误差。比较图5和图6可见：图6中各时刻的相对误差明显比图5中的相对误差大。对于同一天，晚上时刻的相对误差比白天时刻的相对误差大。对每个逐时冷负荷的实际值与预测值相对误差进行统计结果分析，如表1所示。其中：工作日的相对误差为2006-07-14和2006-07-17的平均相对误差，而周末的相对误差为2006-07-22和2006-07-23的平均相对误差。从表1可以看出，周末的冷负荷相对误差比工作日的相对误差要大，这可能周末负荷主要来自商场和酒店，这2个区域的用冷量主要受人流量的影响，而人流量受天气状况、生活习惯等影响，因变数较多而难以预测；工作日的负荷主要来自商务办公，而这部分负荷较稳定，故工作日的预测负荷相对误差小。同理，晚上段的相对误差总比白天段的相对误差大。

表1 冷负荷预测值的相对误差Table 1 Relative error of predict value

3 结论

(1) 系统总冷负荷与用冷区域的功能密切相关：对于商务办公区域，则与工作人员的上下班时间相关；对于酒店区域，则与睡眠习惯相关，对于商场区域，则与气候特点及城市的交通环境相关。建议在选择区域供冷系统设计负荷时，有必要结合当地的工作习惯和生活习惯进行考虑。

(2) 区域供冷系统的实际负荷运行时间分布与单区域供冷系统“负荷越大则运行时间越短”的特点不同，高负荷运行时间较长，在各负荷区间的运行时间分布较均匀。区域供冷系统负荷分布均匀，有利于优化制冷主机的选配和运行，为区域供冷系统高效运行提供理论依据。

(3) 区域供冷系统往往24 h连续工作，全天负荷变化范围大，测试日最低负荷仅为当日最高负荷的11.8%，要求区域供冷系统主机有更合理运行方案才能保证区域供冷系统的节能高效。

(4) 通过改进人工神经网络算法得到的负荷预测值能较好地与实际负荷吻合，反映出实际负荷变化规律，其相对误差与用冷区域功能和特点相关：工作日的负荷预测值相对误差比周末的小，晚上的负荷预测值相对误差比白天的大。

[1] Vrachopoulos M G, Filios A E, Fatsis A, et al. Determination of the thermal and cooling needs of the broader region of Athens[J].Renewable Energy, 2008, 33(12): 2615-2622.

[2] Aktacir M A, Buyukalaca O, Bulut H, et al. Influence of differentoutdoor design conditions on design cooling load and design capacities of air conditioning equipments[J]. Energy Conversion& Management. 2008, 49(6): 1766-1773.

[3] Corgnati S P, Perino M, Fracastoro G V. Experimental and numerical analysis of air and radiant cooling systems in offices[J]. Building and Environment, 2009, 44(4): 801-806.

[4] 杨培志, 陈焕新. 吸附式制冷系统运行参数动态特性[J]. 中南大学学报: 自然科学版, 2008, 39(3): 495-463.YANG Pei-zhi, CHEN Huan-xin. Dynamic operating characteristics for adsorption refrigeration[J]. Journal of Central South University: Science and Technology, 2008, 39(3):495-463.

[5] 王磊, 王锦, 王智伟. 预测参数的选择与建筑物逐时冷负荷的预测[J]. 西安科技学院学报, 2003, 23(1): 23-26.WANG Lei, WANG Jin, WANG Zhi-wei. Selection of prediction parameters and prediction of hourly cooling load of building[J].Journal of Xi’an University of Science and Technology, 2003,23(1): 23-26.

[6] Ben-Nakhi Abdullatif E, Mahmoud Mohamed A. Cooling load prediction for buildings using general regression neural networks[J]. Energy Conversion & Management, 2004,45(12/13): 2127-2141.

[7] HOU Zhi-jian, LIAN Zhi-wei, YAO Ye. Cooling-load prediction by the combination of rough set theory and an artificial neural-network based on data-fusion technique[J]. Applied Energy, 2006, 83(9): 1033-1046.

[8] Dotzauer E. Simple model for the prediction of loads in district-heating systems[J]. Appl Energ, 2002, 73(3/4): 277-284.

[9] Kodogiannis V S, Anagnostakis E M. Soft computing based techniques for short-term load forecasting[J]. Fuzzy Sets and Systems, 2002, 128(3): 413-426.

[10] See L, Abrahart R J. Multi-model data-fusion for hydrological forecasting[J]. Computers and Geosciences, 2001, 27(8):987-994.

[11] TANG Xiao-wo, ZHOU Zong-fang, SHI Yong. The variable weighted functions of combined forecasting[J]. Computers and Mathematics with Applications, 2003, 45(4/5): 723-730.

[12] Kawashima M, Dorgan C E, Mitchell J. Optimizing system control with load prediction by neural networks for an ice-storage system[J]. American Society of Heating Refrigeration and Air Conditioning Engineers Transactions, 1996,102(1): 1169-1178.

[13] Marin F, Garcia-Lagos F, Joya, G, et al. Global model for short-term load forecasting using artificial neural networks[J].Generation, Transmission and Distribution, 2002, 149(2):121-125.

[14] Masatoshi S, Kosuke K, Satoshi U. Cooling load prediction in a district heating and cooling system through simplified robust filter and multilayered neural network[J]. Applied Artificial Intelligence, 2001, 15(7): 633-643.

[15] 施灵. 多台冷水机组空调系统的优化控制[J]. 暖通空调, 2005,35(5): 79-81.SHI Ling. Optimization control stragegy in air conditioning system with multiwater chillers[J]. Heating Ventilation and Air Conditioning, 2005, 35(5): 79-81.