基于循环谱相关方法的MFSK信号识别

孟玲玲,李 静

(燕山大学信息科学与工程学院河北秦皇岛066004)

0 引言

随着通信技术的发展以及通信信号调制样式的复杂多样,如何有效地识别这些信号,在信号确认、干扰识别、无线电侦听、电子对抗、信号监测和威胁分析等军用和民用领域都具有很重要的意义。已往的调制信号自动识别算法较多,有基于信号瞬时频率特征的调制方式自动识别算法[1]、基于星座图的数字调制方式自动识别算法[2]、基于准优化对数似然比的调制方式识别算法[3]等等。这些算法通常都是在信噪比较高时才能对信号进行识别,在信噪比降低到10 dB以下时识别率明显下降。

在实际应用中,通信信号应当被看作是一类特殊的非平稳信号,其一阶或二阶统计特征(均值、自相关函数等)常表现出时间周期性,也就是说这种过程为循环平稳过程。循环谱相关就是建立在这种信号模型基础之上的。利用循环谱相关对高斯噪声不敏感的特性,可以在有干扰和噪声的背景下对信号进行检测、分类。鉴于循环谱相关有以上特性,所以研究用循环谱相关的方法来对MFSK信号进行识别很有意义。此外,通过循环谱相关方法还可以获得载波、脉冲速率以及相位等相关信息[4-5]。

1 循环谱相关函数定义[6]

令x(t)是一个循环平稳信号,其相关函数表示为：

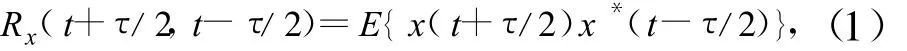
由于Rx(t+τ/2,t-τ/2)是周期为 T的周期函数,将其展开成Fourier级数形式：

且Fourier系数：

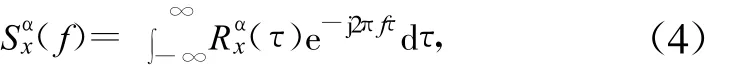
Sαx( f)称为循环谱密度(CSD)。

通常情况下Rαx(τ)写成如下形式：

令

则

在实际应用中,只能根据有限个数据或者说有限的观察时间内的x(t)来近似估计循环谱相关密度函数,常用的方法有离散时域平滑周期图法和离散频域平滑周期图法,本文采用离散频域平滑方法。表达式如下：

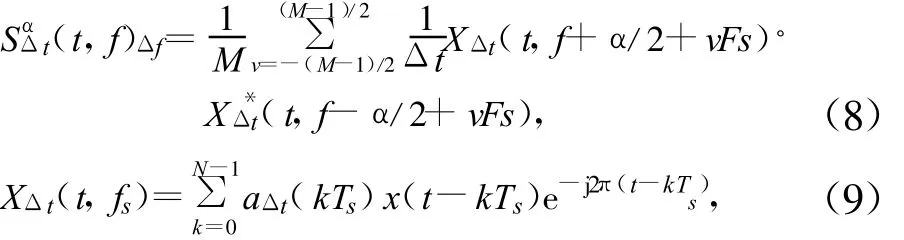
式中,Δf=MFs是频域平滑窗宽度,Fs=1/NTs为频域取样宽度,Ts为时域取样宽度,N为Δt时间内的总采样数,Δt=(N-1)/Ts是数据总长度,ΔtΔf≈M＞＞1满足可靠性条件。

2 频移键控FSK调制信号的循环谱相关性

频移键控FSK信号按载波相位相关性可分为两重情况,一种是相位相关的,另一种是相位随机波动的。

2.1 相位相关的FSK

每个载波脉冲开始时都有一个相同的相位 φm,FSK信号可表示为：

若

则

MFSK的谱相关密度函数为：

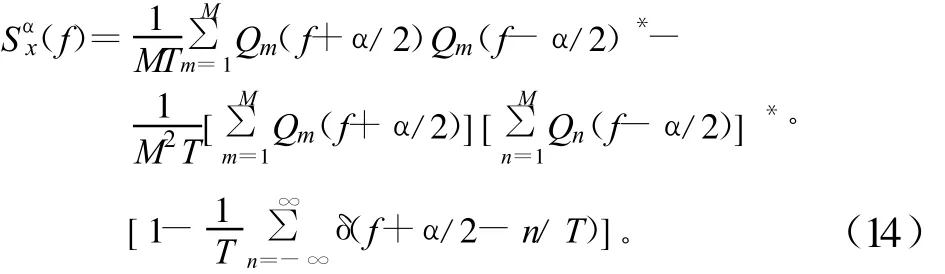
2.2 相位无关的FSK信号

此时码元间的相位是随机波动的,FSK信号可表示为：

如果{θn}是一个独立的序列,在区间[-π,π]上具有均匀的时间间隔分布,并且统计上与{f(n)}无关,则这种FSK信号的循环自相关：

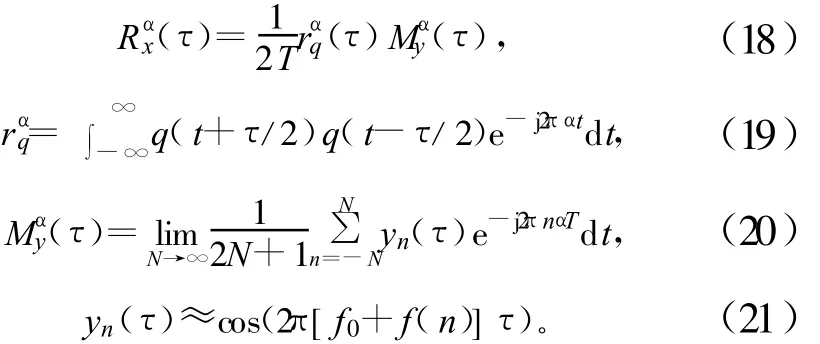
如果f(n)是纯稳态的,并且具有离散的时间间隔分布 PmM1,则：

相位不相关FSK信号的循环谱相关为：

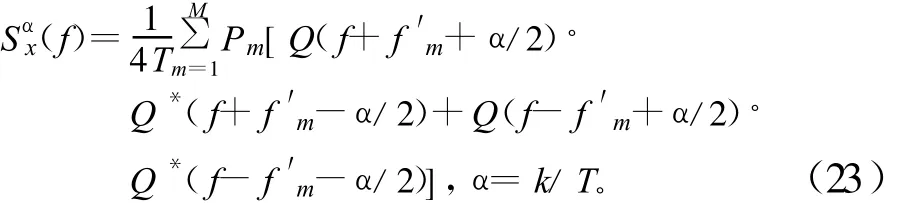
2.3 FSK循环谱相关性能仿真

本文用matlab软件对信号进行仿真,介绍了2FSK,4FSK,8FSK,16FSK四种信号谱相关特性,由于信号谱相关的对称性,为便于分析提取特征谱S0x(f)大于0的部分,且对幅度进行归一化处理。

在没有噪声的情况下 2FSK、4FSK、8FSK、16FSK的特征谱S0x(f)如图1所示。

在信噪比为10 dB的情况下2FSK、4FSK、8FSK、16FSK的特征谱S0x(f)如图2所示。

由图1和图2可以看出各信号的特征谱S0x(f)在f轴上的谱线条数不同,2FSK信号的特征谱S0x(f)在f轴上的谱线条数为2条,4FSK谱线条数为4,而8FSK的条数大于4,16FSK谱线条数也大于4,在信噪比较小的情况下该特征仍十分明显,且特征谱线条数不受载波频率大小和采样频率大小的影响。

图1 理想情况下S0x(f)的幅值平面图

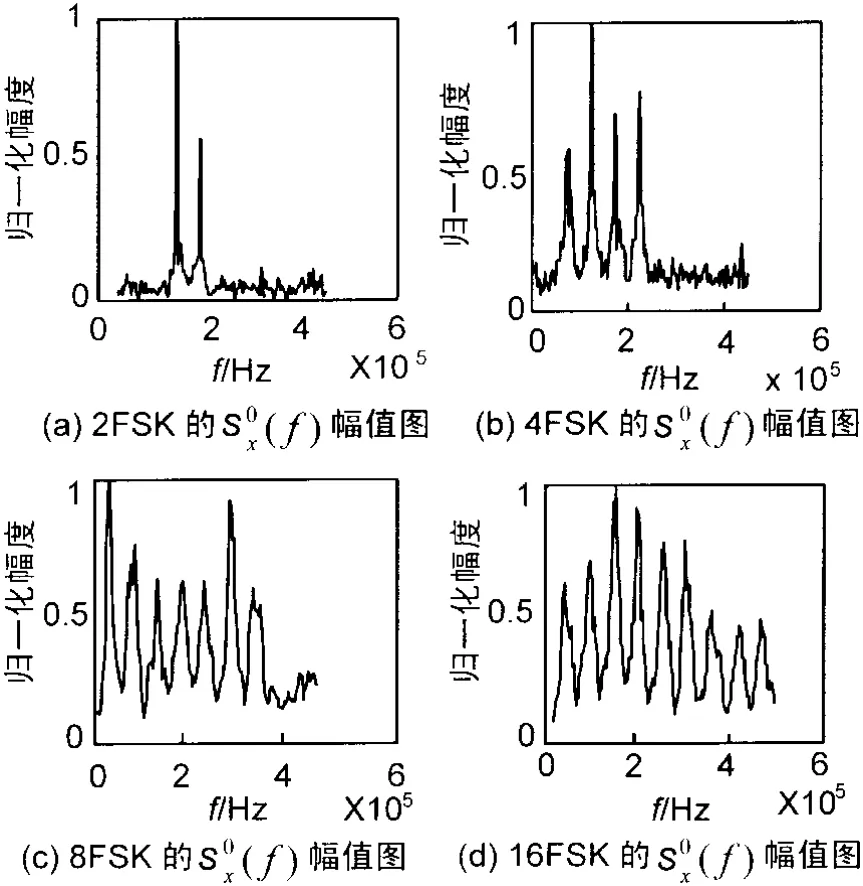
图2 含噪情况下S0x(f)的幅值平面

3 MFSK调制信号的自动识别

3.1 特征参数的选取

根据MFSK信号特征谱的一般性规律,可以利用特征谱S0x(f)在f轴上的谱线条数n作为特征参数来对信号进行识别。对特征参数 n,需要提取特征谱S0x(f)在f∈[0,+∞)轴上含有谱峰的个数,为提取谱峰,必须首先得到光滑的谱曲线。为准确提取特征值谱峰条数n,采用具有高分辨性的自回归(AR)建模方法对谱进行估计[7]。

通过分析离散谱一阶差分序列的符号变化就能检测出谱峰[9]。设

式中,Np为样本总数,Px(n)为n点的信号幅度,如果dp(n)＞0,且dp(n+1)<0,就可确定在频率段[nfs/Np,(n+1)fs/Np]间存在谱峰。谱峰的位置可以线性插值公式计算：

理想情况下可以直接根据公式得出谱线条数n,在有噪声的情况下,尤其是信噪比较小时,n的识别会有很大误差,需要确定一个适当的门限值来减小噪声影响。从理论上分析特征谱谱线幅度大于噪声幅度,但是二者都是随机变量,幅度大小不定,所以仅比较特征谱谱线幅度与噪声幅度不能找到合适的门限值。为了精确得到谱线条数n,本文选取特征谱幅度均值的倍数作为域值,仅对大于阈值部分计算求取 n值。在识别2FSK和4FSK时由于噪声以及谱估计所选阶数不同等的影响还有可能出现n=3的情况,这时仅凭n没法识别信号。为了在这种情况下识别信号,引入另一个特征参数Ad,Ad为归一化谱线幅度的均值。因为条件相同的情况下,2FSK的特征谱幅度明显大于4FSK的特征谱幅度。

3.2 MFSK信号识别流程

根据以上特征参数可得信号识别方法,如图3所示。

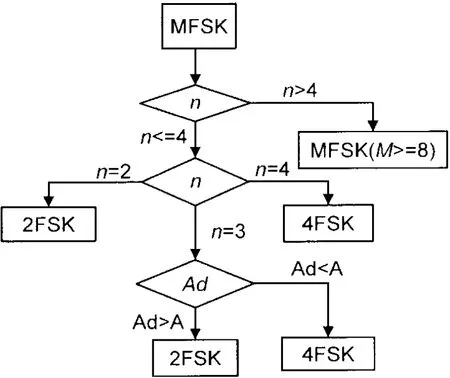
图3 MFSK信号识别流程图

3.3 仿真实验结果分析

在信噪比分别为5 dB和10 dB情况下,对每种信号进行500次实验,载波频率为150 kHz,码元速率为25k,采样频率为1 200 kHz,在进行循环谱相关计算时采样点N=4 096,M=16,识别过程中A=0.6。

表1 MFSK信号识别率

由结果可以看出该算法在信噪比SNR分别为10 dB和5 dB时识别率都较高。

4 结束语

本文利用循环平稳信号的特性循环谱相关理论对MFSK信号进行识别,根据循环谱相关特性提出了一个能有效区分MFSK信号的信号识别算法,实验证明了该方法在识别 2FSK、4FSK和 MFSK(M≥8)信号时的可行性和有效性。但是计算循环平稳信号谱相关时需要的点数很多,计算量相当大,如何优化算法提高运算速度仍是非常重要的研究课题,在信号识别时如何更好地降低噪声影响,更精确地识别信号仍需进一步的研究。

[1]NANDI A K,AZZOUZE E.Algorithms forautomatic modulation recognition of communication signals[J].IEEE Trans Commun1998,46(4)：431-436.

[2]王建新,宋辉.基于星座图的数字调制方式识别[J].通信学报,2004,25(6)：166-173.

[3]HUANG Y,POL YDOROSA.Likelihood metheds for MPSK modulation classification[J].IEEE Trans Commun,1995,43(2/3/4)：1493-1504.

[4]GARDNER W A,BROWN W A,CHEN C K.Spectral correlation of modulated signal：part1-analog modulation[J].IEEE Trans Commun,1987,35(6)：584-594.

[5]GARDNER W A,BROWN W A,CHEN C K.Spectral correlationof modulated signal part2-digital modulation[J].IEEE Trans Commun,1987,35(6)：595-601.

[6]张贤达.非平稳信号分析与处理[M].北京：国防工业出版社.

[7]胡广书.数字信号处理—理论.算法与实现[M].北京：清华大学出版社,1997：342-364.

[8]韩国栋.调制分析与识别的谱相关方法[J].系统工程与电子技术,2001,23(3)：34-36.

[9]王瑛.基于谱相关和神经网络的调制信号方式识别[D].东南大学,南京,2007 ：34-35.