一种BPSK信号符号速率估计算法FPGA实现

李天保,胡 亚

(中国电子科技集团公司第五十四研究所,河北石家庄050081)

0 引言

确定目标信号的符号速率是无线侦收解调的前提条件之一。在软件无线电、电子对抗和无线电侦察等领域都是一项重要的技术。

在软件无线电领域中,无线电台具有多频段、多功能、多体制特性,使得收信方在没有事先约定的情况下无法在特定调制方式下守候接收。因此需要首先对接收信号进行调制信号参数的估计,进而实时重构软件无线电接收机,实现自动接收。而符号速率是数字调制方式的重要参数,符号速率的准确估计对于定时同步、解调有重要意义。

在实际应用中发现对于高速跳频、短时突发等信号,可获得的码元个数有限,这就给符号速率估计,特别是低符号速率的实时估计增加了难度。因此需要对符号速率估计的方法作些改进。在用FPGA硬件实现算法的方案中,则需要综合考虑性能、实时性和硬件资源的限制等因素。

1 算法分析

一种传统的符号速率估计方法是通过直接提取基带信号包络中的重复频率来获得调制信号的符号速率值。

BPSK调制信号可以表示为：

其中,

式中,Ts为符号周期,符号速率rs=1/Ts,fc为载波频率,g(t)是宽度为 Ts的基带脉冲,θc为载波初相,θk等于0或π。

BPSK调制信号经过正交下变频后成为基带I/Q两路信号。

式中,fe为剩余载波,θe为载波与本振的相差。通过计算瞬时幅度可以得到BPSK信号的包络：

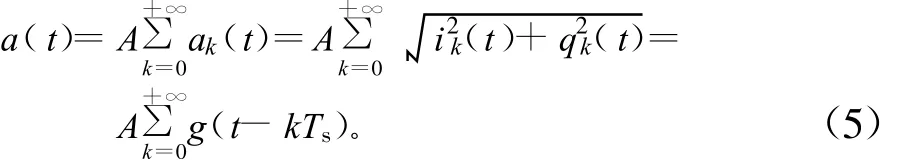
由公式(5)可以看出,BPSK调制信号的包络是由基带脉冲组成的以 Ts为周期的周期函数。当采样点足够多时,随着采样数据中包含的符号数增加,基带信号包络会呈现出周期性,而重复频率就等于符号速率,这是由信息源中0和1的等概率出现所导致的。

基于这样的一种特性,可以对包络作FFT,FFT结果中最大谱线的位置就应等于包络的重复频率,即BPSK调制信号的符号速率。

文献[2]对这一方法进行了理论分析。对循环平稳信号施加非线性变换不仅可以产生符号速率谱线,还会转变出不利于谱线提取的背景噪声,且噪声能量主要分布在低频部分。

在对短数据条件下的BPSK信号作符号速率估计的工程实践中也发现同样的问题。由于采集到的符号数较少,基带信号包络的频谱中低频噪声成分甚至高于符号速率谱线幅度,导致估计错误。

对出现导致符号速率估计错误的频谱图进行分析后可以看出,幅度高于符号速率谱线的噪声分量全部集中在低于符号速率的频率区域。而且在邻近符号速率的范围内噪声分量明显较低。因此仅从视觉上仍然可以辨别出符号速率谱线的位置。

文献[2]利用以上的分析结果对算法进行改进。提供了算法改进公式并进行仿真,对性能改善效果作了评估。噪声抑制算法用公式表示为：

式中,a(k)为原始幅度谱,a′(k)为经过处理的幅度谱,w为窗口宽度,L为FFT点数。

在a′(k)中直接求取最大值点就可以得到符号速率谱线位置。

Matlab仿真结果显示数据观察长度越短,性能改善越明显。当 N=1 024时,性能改善约7.5 dB,而N=512时,性能改善不低于11 dB。

2 设计方案

根据算法分析结果,符号速率估计首先需要对中频采样数据进行正交数字下变频,变换成为I/Q两路基带调制信号的数据流。再从中获得包络信息,符号速率谱线就存在于包络的频谱中。因此整个符号速率估计的设计方案框图如图1所示。

图1 符号速率估计的设计方案框图

在图1中首先对中频BPSK调制信号进行采样,将采样结果送入FPGA进行符号速率估计。

数字下变频包括数字正交混频和滤波抽取两部分。正交混频的目的是将实信号变换成为解析信号,可以方便地从中获取瞬时幅度。在目标信号符号速率种类较多的情况下,采样信号中还包含信号带宽以外的噪声分量,需要进行滤波,滤除带外噪声。

从数学公式来看,计算瞬时幅度的方法就是求取I/Q两路信号的平方根。计算瞬时幅度产生的数据流就形成了BPSK基带信号的包络。从算法分析中可以得知,该包络中就包含了符号速率的频率分量。因此对包络作FFT处理,获得幅度谱,在符号数足够多的情况下,幅度谱中最高的一根谱线所在的位置就对应于符号速率。

对于符号数较少的情况,幅度谱中存在色噪声,且色噪声的幅度可能高于真实符号速率位置处的谱线高度,直接用寻找最大值的方法无法正确估计出符号速率,需要对幅度谱作噪声抑制的处理。根据色噪声的特点,噪声抑制的方法就是对幅度谱中的每个点除以其右侧若干个点的平均值,形成抑制后的频谱图,再利用寻找最大值的方法就可以得到正确的符号速率值。

3 设计实现

3.1 数字正交下变频

首先利用查表法产生数字本振,即事先根据各个正/余弦波的相位计算好相应的正/余弦值,并按照角度作为地址在FPGA内部存储器中对其进行寻址,构成一个幅度/相位转换电路,通过该转换电路进行查表获得正/余弦样本。中频采样实信号在FPGA内部通过硬件乘法器同时与2个正交的数字本振相乘后就产生了正交混频数据流。数字正交下变频的原理框图如图2所示。

图2 数字正交下变频实现框图

为了适应不同符号速率,还需要对混频后的数据进行多级滤波抽取。根据前端估计出来的信号带宽参数,选择最符合该信号带宽的滤波器节点作为输出。滤波器可以采用IP核来实现,滤波器系数用MATLAB软件中数字处理工具就可以产生。

在整个正交下变频模块中,正交本振序列的产生、数字混频以及滤波抽取都是数学运算的结果,且工作在同一时钟域内,因此结果的正交性是完全可以得到保证的。但由于是定点运算,无论是混频还是滤波,都会使数据位宽增加。为了既确保运算精度,又能尽量减少资源占用,需要进行仿真以截取合适的位宽。

3.2 幅度计算

在设计方案中无论是计算正交下变频结果的瞬时幅度,还是计算FFT结果的幅度谱,都涉及到开平方这样的超越函数计算,直接用乘加的方法不能直接得到。在FPGA内部通常采用坐标旋转数字计算机算法(CORDIC)。CORDIC在FPGA内有成熟的IP核可以利用,精度高,其缺点是在流水线模式下时延较大,但对于数据流处理选择CORDIC没有影响,因此选择CORDIC方法更为便捷。

3.3 FFT处理

FFT处理在FPGA中有IP核可以利用,但需要对FFT的点数和模式进行设置。FFT的点数可以根据符号速率估计的精度要求进行选择。而由于实时处理的需要,FFT的模式需要选择块浮点流水线(PIPELINE)模式FFT。在这种模式下,能够以固定的时延计算出每一帧输入数据的频谱,可以满足实时性的要求,缺点是占用资源较大。因此可以在满足符号速率估计精度的前提下尽量减小FFT点数,以减少FPGA资源的占用。在低符号速率下,经滤波抽取后在一跳的时间内积累点数不足设置的FFT点数时,需要在有效数据后补0处理。

FFT模块输出结果由实部、虚部和指数项组成,由于后面的估计处理只需要得到幅度谱,可以利用前面的CORDIC模块计算幅度。虽然FFT输出结果为块浮点格式,结果还包含指数项,但对于一帧数据而言,这个指数项是固定的,对于后面的寻找符号速率频率成分比较大小而言没有影响,所以在计算幅度时不必考虑指数项。此外,对于后面的处理,用求平方和来代替求幅度从MATLAB仿真结果来看都是一样的效果,但平方和后数据位宽加倍,后面的处理需要占用更多的资源,所以仍然可以采用CORDIC方法。

3.4 噪声抑制

首先设置一个固定点数的窗口,对窗口内谱线幅度值取平均,再将靠近滑动窗左侧谱线除以该均值。让该窗口在频谱图中从高频向低频逐点滑动,从而形成一个经过处理后的频谱。在具体实现上,以16点宽度的窗口为例,首先需要将FFT运算结果存储双口缓存中。FFT模块输出数据同时也将对应点序号同步输出,将该序号值作出与求幅度模块相同的时延后就与幅度谱数据一一对应起来,以该序号为地址存入缓存中。由于频谱的正负对称性,序号大于一半点数的数据丢弃不用,这样就得到了存储着正频率部分幅度谱数据的缓存。设置一个初始值为一半点数的递减计数器,以该计数器为地址从缓存中读出幅度谱数据,同时统计出前16个点的平均值,用当前值除以该平均值,把结果存入另一个缓存当中。计数器归0后就得到存有处理后的频谱结果的缓存。

由于处理中用到除法,而直接作除法运算在FPGA中难以实现,在具体实现上有2种方法可以作近似处理。一种方法是用查表法将幅度谱取对数,把除法转换成减法;另一种方法是用右移位把被除数转换成与之最接近的2的整数次幂,实现近似除法。显然前一种方法的精确度更高,但实现的复杂度更大。

3.5 最大值检测

最大值检测在FPGA内部实现相对较为简单,与软件方法较为类似。由于在噪声抑制模块中已经将噪声抑制处理后的数据缓存于内部双口RAM,依次读出并比较即可得到最大值。

3.6 延时控制

由于整个符号速率估计需要较大的时延,为了将采样结果与符号速率估计结果对齐,需要将采样数据存入一个足够大的FIFO中。当符号速率估计完成了一帧数据的处理后,在最大值检测模块输出最终结果,同时利用输出脉冲触发启动FIFO的读操作,从而实现了中频原始数据与符号速率的同步输出。

4 实际效果

图3是噪声抑制前后的频谱图,数据来自实际信号经FPGA处理的中间结果,在FPGA内部缓存后经监控读取获得。

图3 噪声抑制前后幅度谱比较

从图3可以看出在噪声抑制处理之前,符号速率谱线与左侧色噪声包中的谱线相比并不是最大值,用最大值检测的方法无法获得正确的符号速率估计结果。但经过噪声抑制后,符号速率所在位置的谱线成为频谱中的最大值,用最大值检测模块就可以得到正确的估计结果。

5 结束语

设计中采用的器件是Xilinx公司的Virtex5系列XC5S95T-2型FPGA芯片,算法实现的工作频率大于200MHz,设计充分考虑了FPGA实现的可行性以及对实时性、实现精度和资源占用的要求。经实验证明,能够成功实现在中等信噪比下、码元个数为64个以上的符号速率的估计,已应用于某无线侦察系统中。

[1]管吉兴.FFT的FPGA实现[J].无线电工程,2005,35(2)：43-46.

[2]张晓勇,罗来源,罗武忠.一种基于瞬时幅度的PSK信号符号速率估计方法[J].信号处理,2008,24(2)：316-319.

[3]刘双平,闻翔,金梁.一种抑制符号速率估计背景色噪声的非线性滤波算法[J].电子学报,2007,35(1)：95-99.