圆管大应变分析的自适应单元网格划分技术

张博利

（中国民航大学基础实验中心，天津 300300）

近十多年来，全球范围内的恐怖爆炸袭击事件不断上升，已构成对城市乃至国家的重要威胁。政府办公和重要的基础设施已成为恐怖袭击的重要目标。机场作为重要的基础设施，现已成为恐怖袭击的重点对象。爆炸恐怖袭击是最常见而且容易实施的重要手段，像汽车炸弹、邮件（包裹）炸弹、人体炸弹、固定箱包炸弹等方式。由于汽车炸弹相对携带的爆炸物多一些，即使在与机场一定距离处爆炸，也可对机场进行毁灭性的破坏。然而其他三种炸弹，可通过严格的安全检查措施加以控制。由于近距离爆炸作用于建筑物的冲击波荷载非常大，可导致建筑物严重的破坏。因此对于机场来说，对汽车炸弹的防范成为重中之重。机场防恐防爆的主要目的是航站楼不会倒塌，减小结构产生的整体破坏，控制产生次生杀伤的飞片。由于航站楼结构设计的特殊性，不适合在四周设置防护墙。安装防撞杆可以起到与设置防撞墙同样的作用，并且防撞杆易于成型，坚实实用。本文对防撞杆进行安全性分析，并利用LS-DYNA软件对它进行碰撞模拟实验，以期为防撞杆设计提供参考。

Ls-dyna软件是世界上最著名的通用显示非线性动力分析程序，能模拟真实世界的各种复杂几何非线性（大位移、大转动和大应变）、材料非线性和接触非线性问题，特别适合求解各种二维、三维非线性结构的高速碰撞、爆炸和金属成形等非线性动力冲击问题。

1 非线性有限元理论

圆薄壁钢管在冲击作用下的屈曲过程是一个动态的大位移和大变形的过程，接触状态和冲击载荷都影响着屈曲的全过程，系统具有集合非线性和材料非线性等多重非线性。一般的线性有限元方法都基于线性的小位移系统，本例题所研究的系统模拟计算则需要采用动态大变形非线性有限元方法。

1.1 物体变形状态的描述

由于物体在变形前后发生很大的变形，因此必须考虑物体受力前后在空间位置上的改变。

为了描述物体变形前后两种不同状态，须引入参考状态和变形状态。在某一瞬时，物体在空间所占据的区域称为物体的构型（Configuration）。令在时间t=0时，物体的初始构型为V0，参考于一固定的直角坐标系{xi}，物体的任一质点P的位置可由一向径p（x1，x2，x3）或其质点坐标 x1，x2，x3确定。构型 V0称为物体的参考状态。在后来某一瞬间t，物体被移动到空间的另一位置，其构型为V，这时的状态称为变形状态。描述这一变形状态，用另一直角坐标系（yi）。初始构型中的P点，变形后被移动到空间的P点，可由一向径p（x1，x2，x3）确定。如果令坐标系（xi）和（yi）重合，则在二维情况下同一个质点变形前后的关系

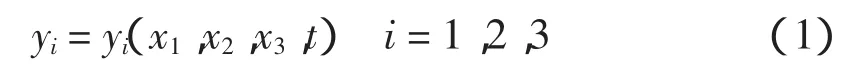
其中，yi是x的单值连续函数，且雅可比行列式（Jacobi）的值不等于 0。

如果ui为质点xi轴方向的位移，那么

或写成向量形式：

在描述物体变形前后的不同状态时，有如下两种方法。

1.2 拉格朗日（Lagrange）描述

x1，x2，x3和t作独立变量来描述物体的运动（或变形），称为物体描述（material description）或拉格朗日（Lagrange）描述，而 x1，x2，x3和 t称为拉格朗日变量，上述式（1）～式（3）就是这种描述形式。此种描述是以变形前的状态，即以己知的初始构型为V0参考状态，随着运动的质点研究质点的运动状态。在描述状态中其中p代表坐标为x1，x2，x3的质点，是不随着时间t变化的。vt表示速度表示加速度，M表示质量，p表示质点轨迹，ρ0（p）是构型V0在p点处的密度。

1.3 欧拉（Euler）描述

取y1，y2，y3和t作为独立变量来描述物体的运动（或变形），称为空间描述（spatial description）或欧拉（Euler）描述，y1，y2，y3和 t为欧拉变量。空间描述是以当前的构型V为参考状态，研究空间各个不同的质点经过空间某一定点y1，y2，y3时的状态。在描述状态中，，其中，p 代表坐标为 y1，y2，y3的质点，vi表示速度表示加速度，M 表示质量，V表示质点轨迹，ρ0（p）是构型V在点p处的密度。

在碰撞模拟计算中接触问题的处理是一个重点，接触问题的处理实质上就是接触力的计算，对于接触力的计算主要采用罚函数法与拉格朗日乘子法。罚函数法虽然只是近似的满足接触碰撞边界条件，但是容易实现，并与显示算法完全相容，因此在实践中得到广泛的应用。本文求解接触碰撞问题所用的LS－DYNA有限元软件就是采用罚函数法确立接触界面的。

2 有限元模型的建立

某种防撞杆的结构具体参数如下：圆钢管直径D=300 mm，壁厚 t＝2.5 mm，长度 L=1 000 mm，一端完全固定，另一端施加载荷。模拟分析采用10 ms内施加0.4 N的力，分析钢管在整个过程中的变形及应力分布情况。钢管底端为固定端，约束所有的线位移自由度，钢管顶端除UZ方向外，其余全部约束。由于钢管表面在冲击压缩过程中，可能发生表面折叠和自相接触现象，需定义为单面接触算法ASSC，接触面的摩擦系数为0.1，求解时间为0.015 s。

表1 材料参数Tab.1 Material parameters

表2 冲击载荷数组Tab.2 Array of impacting loading

采用固定网格划分后，在冲击后钢管0.008 24s时的变形和应力情况，如图1所示：

由于薄壁管在冲击作用下，将发生极大的塑形变形，管件内部的等效应变和等效应变率分布是不均匀的，且应变集中在某些区域，这导致在网格中只有小部分单元格发生干涉或严重变形，而大部分单元格尤其是内部单元格的质量依然良好。因此当检测到网格中发生畸变或干涉后，可以先只对少量畸变或干涉单元进行局部调整。在有限元计算欧拉方法中，计算网格固定于几何空间，材料通过流进流出，计算单元质量、动量和能量的变化，从而确定物体的变形。欧拉方法能够处理材料严重的扭曲变形，但很难跟踪物质的变形，不能识别材料界面，计算材料的弹塑性不够精确。拉格朗日方法把计算固定在材料上，可以跟踪物质的运动，能够清楚地识别材料的边界和交界面，并且具有较高的计算速度和精度。然而对于有较大的网格畸变，材料破碎使得简单连接区域变成多连接，以及网格重叠造成负质量时，将导致时间步长缩小，求解精度降低，甚至停止计算，解决这个问题的好方法就是采用自适应网格方法。

自适应网格方法是指在计算某些变化较为剧烈的区域，如大变形、激波面、接触断面和滑移面等，网格在迭代过程中不断调节，将网格细化。做到网格点分布与物理解的耦合，从而提高解的精度和分辨率的一种技术。自适应网格希望在物理解变动较大的区域网格自动密集，而在物理解变化平稳区域网格相对稀疏，这样在保持计算高效率的同时得到高精度的解。在LS-DYNA中，自适应网格划分方法分为二种：hadaptive方法和r-adaptive方法。h-adaptive方法是指单元变形较大时，将单元分为更小的单元以改善精度，仅适用于壳单元，主要用于金属成型模拟、薄壁结构受压屈曲等问题。r-adaptive方法也称重分区技术或者自适应网格部分，是指重新移动和划分单元，将网格节点重新排列，得到时步长内最优纵横比。

LS-DYNA采用自适应网格方法的目的在于使用有限的资源获得最大的计算精度。用户设置好了初始网格和自适应划分级别后，程序根据需要将某些单元进行分割。虽然这种方法不能完全解决过程中的误差，但与固定网格相比，可以使用较少的单元和计算资源来获得尽可能高的计算精度。

薄壁圆钢管在冲压过程中，采用的是h-adaptive方法。只是将固定网格通过裂变，细分成更小的单元。裂变是指某些单元由于精度需要细分为更小的单元，如图2所示。裂变后，新的边长尺寸是原来的1/2。本例采用的是3级网格细化。细化后，钢管的在同一时间的压缩情况和特定单元的应力都将发生变化，如图3所示。

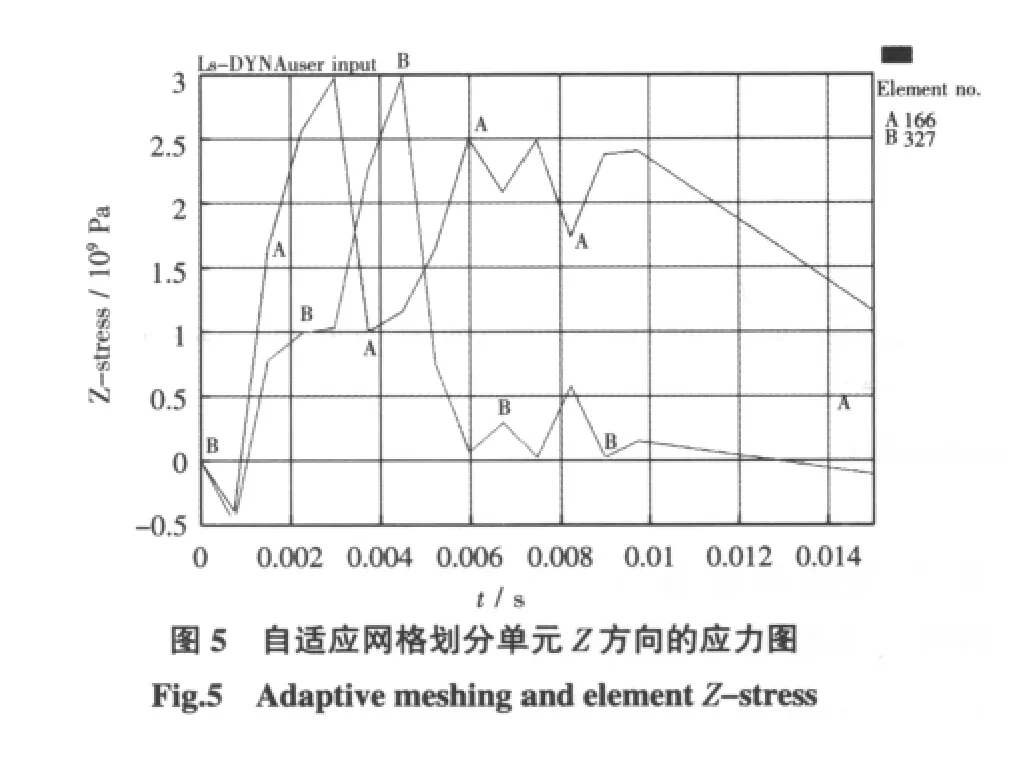
在图4和图5中，A代表圆管压缩过程中变形较小的单元，B代表圆管压缩过程中变形较大的单元。通过二图中A曲线的比较，在如图4所示的固定网格划分的情况下，Z方向的应力变化不大。而在图5自适应网格划分后，由于网格个数的增多，Z方向的应力变化较大，真实反映了变形较小单元在受冲击过程中的应力随时间的变化情况。在图4和图5中B曲线在0.005 s和0.009 s左右时的应力值几乎达到同一值，说明在采取自适应网格后，在大变形的情况下，最大值和最低值的变化不大，只是对变形过程的反映更加真实化、准确化。

3 结语

通过以上数据可以看到，自适应网格方法的目的在于使有限的计算资源获得最大的计算精度，当设置好初始网格和自适应划分级别后，程序根据需要将某些单元进行分割，虽然这种方法并不能完全解决求解过程中的误差，但与固定网格相比，可以使较少的单元和计算资源尽可能提高求解精度。自适应网格技术在薄板冲压变形模拟，薄壁结构受压屈曲以及机场防撞杆的受冲击等大变形情况中，LS-DYNA程序通过自适应网格剖分功能，使出现大弯曲变形的起皱部分自动加密网格，对计算精度有了显著提高。因此，自适应单元网格划分技术是LS-DYNA处理单元大变形问题的重要手段。

[1]陆 勇，曹立波.对汽车撞柱的仿真研究[J].农业装备与车辆工程，2006（1）：28-31.

[2]田志敏，张想柏，杜修力.防恐怖爆炸重要建筑物的概念设计[J].土木工程学报.2007，40（1）：34-41.

[3]何 涛，杨 竞.ANSYS10.0/LS-DYNA非线性有限元分析实例指导教程[M].北京：机械工业出版社，2007.

[4]尚晓江，苏建宇.ANSYS/LS-DYNA动力分析方法与工程实例[M].北京：中国水利水电出版社，2006.

[5]LAN SHENGRUI，CRAWFORD JOHN E.Development of shallow footing anti-ram bollard system through modeling and testing[J].Transactions of Tianjin University，2006，19：46-50.