铁路路基沉降评估中预测模型的选择

2010-07-30刘俊飞赵国堂

铁道建筑 2010年11期

刘俊飞，赵国堂，2

(1.西南交通大学岩土工程系，成都 610031;2.京沪高速铁路股份有限公司，北京 100038)

新建铁路线下工程沉降评估是针对无砟轨道铺设条件的评估，是通过对线下结构既有沉降观测数据的分析，预测其远期沉降，来判断和检验能够满足工后沉降要求的无砟轨道铺设时机。沉降评估是解决当前设计阶段沉降计算精度不足与无砟轨道线路毫米级工后沉降控制标准之间矛盾的必要途径。随着线下工程施工中和施工后持续的沉降观测，及时进行沉降评估，动态地验证或调整后续施工的时间节点和设计措施，进行信息化施工，是实现新建铁路沉降控制标准的关键手段。这种方法正符合了刘建航院士总结的岩土工程工作方法的十六字诀:“理论导向，实测定量，经验判断，检验验证”[1]。新建铁路设计阶段的沉降计算起着“理论导向”和“经验判断”的作用，而沉降观测与评估则是“实测定量”和“检验验证”。

路基、桥梁等线下工程必需在沉降评估通过后，方可开展无砟轨道铺设施工。相对于桥梁等工程，路基沉降量一般较大，沉降稳定所需时间一般较长，所以路基的沉降评估显得更为重要。

《客运专线铁路无砟轨道铺设条件评估技术指南》(以下简称《指南》)规定:路基沉降根据填筑完成或堆载预压后不少于3个月的实际观测数据作多种曲线的回归分析，进行沉降预测[2]。其条文说明中给出了双曲线法、三点法、抛物线法、指数曲线法、沉降速率法、星野法、Asaoka法、泊松曲线法、灰色理论和人工神经网络等分析方法。此外，还有学者提出一些新的预测方法[5]。

面对这些多种沉降预测方法，如何判断它们的适用性和沉降预测结果的有效性，选择恰当的预测模型是沉降评估工作的关键之一。本文将结合新建铁路线下工程沉降评估中沉降预测的特殊性，对这些预测模型的适用性进行初步分析，并提出预测模型的优选方法。

1 新建铁路路基沉降预测的特殊性

新建铁路路基沉降的预测并非一个完全的“黑箱系统”，只根据现场反馈的数据本身进行推算，它必需考虑到沉降评估工作本身的特殊性。路基沉降预测数学模型的确定需要通过模型实际意义的检验，新建铁路路基沉降预测的特殊性主要表现为以下三点:

1)要求数学模型具备连续性和单调性

恒载作用下沉降量是连续的，并随时间的增加而增加。用数学函数S(t)表示t时刻沉降，则该函数对时间 t求导应 >0，即

若用负数表示沉降值，则式(1)中不等式符号为≤。

2)对远期沉降的预测，要求数学模型具备有界性

恒载作用下沉降速率随着时间的增加不断减小，并趋于稳定。另一方面，沉降评估针对的是工后沉降，这就要求预测出t→∞时的沉降，至少是无砟轨道主体设计年限内(一般不小于60年)的最终沉降量。这就要求沉降预测的数学模型本身能够求取极限，即

其它岩土工程中的沉降预测多为短期预测。例如，建筑基坑工程中通过坑壁附近的沉降观测对基坑侧壁的稳定性进行判断，软土路基填筑工程通过原地面或路基表面的沉降观测对路堤边坡的稳定性进行判断，只需要对一天或数天之内的沉降进行短期预测。在高速公路工程中，也有对工后沉降的预测，其预测时间一般结合道路路面的使用年限，设为15年或20年。

3)对预测的可靠性要求较高

为了保证新建铁路线路的高平顺性和高可靠性，无砟轨道的工后沉降标准十分严格。我国高速公路工后沉降控制标准要求仅为一般路段不大于30 cm，桥头不大于10 cm，与我国普速铁路标准相当。而我国《新建时速300～350 km客运专线铁路设计暂行规定》要求无砟轨道地段路基工后沉降一般不应超过扣件的允许调高量15 mm，并有其它严格的纵向差异沉降的限值要求。

新建铁路除对工后沉降严格要求外，也同时需要在沉降评估中的沉降预测具有较高的可靠性。

2 《指南》中各沉降预测模型分析

《指南》中列出的十余种沉降预测方法可分为两大类:曲线回归分析法和系统科学法。其中，曲线回归分析法都有一定的显式数学表达式，系统科学法则不采用显式数学表达式，而是采用某种系统科学理论对数据进行处理和分析。《指南》中的系统科学法包含灰色理论和神经网络两种。这两种方法都是近些年发展并兴起的新的数学方法。

《指南》明确规定了路基沉降观测的频次，指出回归分析的时间不早于恒载期3个月，并在此基础上提出了检验沉降预测有效性和可靠性的三个标准:①相关系数标准。曲线回归的相关系数不低于0.92。②沉降速率标准。间隔不少于3个月的两次预测最终沉降的差值不大于8 mm。③完成的沉降量标准。路基填筑完成或堆载预压完成后已产生的沉降占预测最终沉降的比例不小于75%[2]。

这三个标准中，相关系数标准仅适用于回归分析方法，而另外两个标准则只是经验性的控制方法。可见，《指南》在预测模型的选择上给了评估人较大的自主空间，需要评估人在多种预测模型之间进行横向比较，进一步优选出适当的预测模型。

因此，有必要首先对《指南》中各种预测模型进行一下总体上的对比和分析。各模型对数据的要求和理论依据的对比见表1。

2.1 系统科学法预测模型分析

1)灰色理论

灰色系统的任务是少数数据建模，目标是微分方程建模，要求动态信息的开发、利用和加工，充分开发利用少数数据中的显信息和隐信息。一般来说，微分方程只适合连续可导函数，而灰色系统的行为特征是用时间序列表征，是一种离散的函数。为建立微分方程模型，灰色系统理论通过关联分析，提取建模所需变量，并在对离散函数的性质进行研究的基础上，实现对离散数据建立微分方程的动态模型，即灰色模型(Gray Model，简称 GM)。

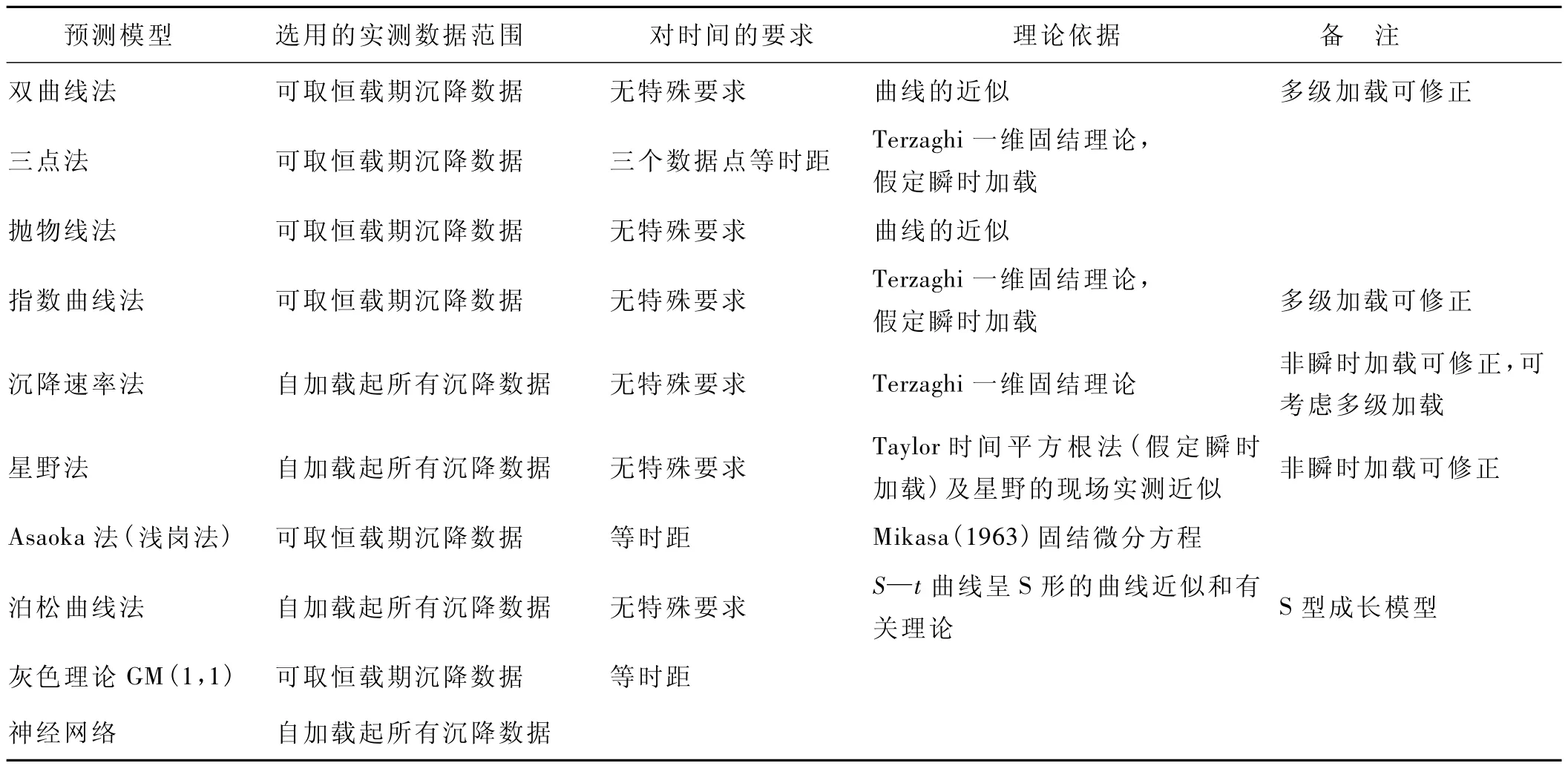
表1 《指南》中各沉降预测模型对数据的要求和理论依据

一般的灰色模型为GM(h，n)模型，表示h个变量的n阶微分方程。在岩土工程有关变形问题的预测研究中，目前用得最多的是 GM(1，1)模型，因为变量越多，阶数越高，计算量就越大，且精度也不一定就很高。GM(1，1)要求数据等时距，因此需要预先对既有沉降数据进行等时距处理，如采用样条曲线上内插的方法获得等时距沉降数据。

由于灰色模型是通过离散函数对时序数据的加工和处理，它并不具备有极限的特征。图1为对某组沉降数据的GM(1，1)预测，可以发现其后期预测值并没有收敛的趋势，沉降反而有所加速，这与地基沉降的自身特征明显不符。虽然该组数据并不满足恒载期不少于3个月要求，但是GM(1，1)对远期沉降预测的不适应性已暴露无遗。可见，GM(1，1)仅在短期沉降预测中可以使用。

图1 GM(1，1)沉降预测示例

2)神经网络

神经网络不需要精确的数学模型，运用由输入层、隐层和输出层组成的神经网络的非线性映射能力，对实测数据进行直接建模，常用的算法有BP算法等。

模仿人脑的学习过程，神经网络预测路基沉降时序问题，需要学习训练和预测两个过程。神经网络能够把地基处理方式、地基土模量与厚度、填土高度等因素纳入“学习”范围，通过数学上的“学习训练”使输出接近实际值。

通过神经网络的学习训练后，当输入值为接近其学习范围时，能够获得较为理想的效果。然而，在沉降评估阶段无法获得实测的远期沉降数据，就世界范围来看，高速铁路也仍是一个新生事物，其它高速铁路的历史性数据也无法获得，因此神经网络对远期沉降的“学习”也无从谈起。这就限制了当前的新建铁路地基沉降神经网络的预测，即仅适用于短期预测。

2.2 曲线回归分析法预测模型分析

回归分析是数理统计学的重要分支，其应用范围十分广泛。回归模型的数学形式可以基于一定的理论推导，也可以根据曲线的近似。由于当前的岩土工程理论和技术水平，并不能通过理论推导来获得准确的S(t)数学模型，因此即使表1中所列的基于一定固结理论的回归分析法模型中的数学形式也只能是近似，仍需要根据实测数据进行回归分析。

《指南》中各回归分析法预测模型都能满足式(1)所表示的连续性和单调性要求。考察各回归分析法预测模型的有界性则发现，除抛物线法外，其它几种回归模型都可以求得极限。

抛物线法来自于文献[10] ，其沉降曲线的一般表达式为

式中，a、b、c为待定常数。其极限无法求得，该函数为发散函数。

究其原因，该方法所列的表达式只适用于对固结曲线前段的拟合，不能将式(3)扩展到 t较大的情况。该文献作者指出，最终沉降量近似等于常数项c。这一结论也缘于经验性的判断，在使用该模型时应予以注意。若沉降评估者无相应经验，不建议使用本模型。

几种回归分析法模型中，三点法与指数曲线法的理论依据完全相同，它们的区别仅在于求解方法的不同:三点法利用三点的数据解方程组(三和值法)求取各参数，而指数曲线法可采用非线性最小二乘获得估计值。在正态误差假定下，非线性最小二乘估计值比三和值更精确[4]。

另外，需要说明的是泊松曲线法，它是一种S型曲线模型。S型曲线模型又称“成长模型”，它表示地基沉降从加载伊始经历了一个“成长—发展—稳定”的过程，沉降曲线呈S形。文献[9] 从理论上证明了线性加载或近似线性加载情况下，沉降—时间曲线呈S形。实践表明，S型沉降曲线多出现于加载过程较慢的软土路基。因此S型成长模型所统计的数据范围包含自加载起所有的沉降数据，而其它回归分析方法常用于恒载期的数据统计。

新建铁路出于沉降控制的需要，在软弱土地基路段均进行了良好的地基处理，路堤填土施工也一般较快，S型沉降曲线并不多见。

3 用残差分析辅助判断预测结果的可靠性

《指南》中用相关系数作为沉降预测可靠性的数学标准。非线性回归的相关系数是比照线性回归中相关系数的方法，采用下式求得

式中，yi为第i个观测值，为回归拟合值，为观测值的平均值，称为残差，记为ei。

文献[4] 指出，对非线性强度很高的回归方程在使用相关指数R2时应慎重。1990年就有人提出 R2不能用于非线性回归方程的评价，目前这一问题的研究已引起一些学者的关注。一般地说，当非线性回归模型选择正确，回归拟合效果较好时，相关指数R2能够如实反映回归拟合效果;而当回归拟合效果较差时，相关指数R2则不能够如实反映回归拟合效果，甚至可能取为负值。

另一方面，对基于数据统计的预测而言，建立回归方程时样本容量越大，预测的精度就越高;预测时所给定的t越靠近样本t的平均值，预测的精度越高。这就要求沉降观测应保证应有的频次，沉降评估时选择的统计数据范围应尽量大，同时要求沉降评估的时间不能太早。

实际工程，沉降观测的频次可以保证需要，沉降观测数据的质量也可以通过技术手段得到保障，这样时间便成为控制沉降预测可靠性的一个关键因素。施工中，轨道板铺设和线上工程各专业施工等大量后续工作需要在沉降评估通过后进行，路基的静置时间过长是客观条件所不允许的。因此需要评估者尽早根据既有数据做出可靠的沉降预测。

下面以新建铁路李窑试验段A区为例，通过对该点沉降曲线拟合特征的分析，研究提高沉降预测可靠性的方法。

李窑试验段A区为滨海相沉积的深厚软弱土地基，采用桩网复合地基加固，桩长24 m。路堤设计填高6.9 m，堆载预压高度3.5 m。该处路基已完成填筑、静置、预压土卸载阶段，沉降观测历时较长，具有一定代表性。该区自填筑施工开始，第16 d完成路堤和堆载预压土填筑，第278 d卸除预压土，第288 d完成预压土卸载。路基中心CFG桩顶沉降观测数据见表2。

从《指南》所列的几种回归分析模型中选取具有代表性的双曲线法、指数曲线法和星野法三种模型分别进行回归分析，曲线拟合结果见图2。双曲线法、指数曲线法和星野法预测得到的最终沉降分别为－48.7 mm、－43.4 mm和－50.2 mm，其相关指数 R2分别为0.985 9、0.987 1和0.969 4。

由图2可以看出，三种曲线具有不同的曲率适应性。其中，指数曲线收敛速度较快。虽然指数曲线法的相关指数最高，但可以看出它的预测值偏小，并不是最可靠的结果。三种拟合方法的残差分布见图3。从图3可见，三种拟合的残差分布都不完全具备正态特征，特别是尾段残差仍有较为明显的增大或减小。这种现象表现了天然土体性质和地基沉降过程的复杂性，所用的函数还不能完全反映沉降发展的规律。另一方面，也可以利用这一现象对长期预测的倾向性进行判断，以提高预测结果的可靠性。

表2 李窑路基试验段A区路基中心CFG桩顶沉降观测数据

图2 李窑试验段A区0～313 d沉降数据拟合结果

如图3，双曲线法和星野法的尾段残差趋于增大，说明当前的最终沉降预测值偏于安全。与之对应，指数曲线法尾段残差趋于减小，说明当前的最终沉降预测值偏于不安全(第278 d后残差变化趋势变缓为预压土卸载所致)。最有可能的最终沉降介于－48.7～－43.4 mm之间，沉降评估使用－48.7 mm作为预测值是可靠的。

图3 李窑试验段A区0～313 d沉降拟合残差分布

图4为李窑试验段 A区由0～105 d(静置期89 d)沉降观测数据拟合得到的残差分布。此时，双曲线法、指数曲线法和星野法得到的最终沉降分别为－51.4 mm、－41.9 mm和－57.6 mm，相关指数 R2分别为0.986 7、0.987 1和0.972 9。由残差分布图尾段1个多月连续的4次观测残差趋势可见，此时的星野法预测值偏于安全，指数曲线法预测值偏于不安全，双曲线法稍偏于安全，可以作为此时的预测值。