强度折减有限元法在路基边坡稳定性分析中的应用

□文/刘海峰 吕 恩

路基边坡稳定性分析是路基设计的重要内容。目前，边坡稳定性分析方法主要有极限平衡法和弹塑性有限元法。极限平衡法需要预先知道边坡滑动面的位置和形状，不能搜索出边坡的危险滑动面及相应的稳定安全系数。单纯的弹塑性有限元法一般只能得出边坡应力、应变、位移等，无法直接得到边坡危险滑动面及相应的安全系数。而强度折减弹塑性有限元法是将强度折减法与弹塑性有限元法相结合[1～3]发展而成的分析边坡稳定性的有效方法。强度折减弹塑性有限元法是不断将路基边坡土体进行强度折减，然后应用有限元法对边坡进行弹塑性分析，得到边坡内的应力、应变、位移等，当边坡土体符合稳定临界状态判定条件时，对应的强度折减系数即为边坡的稳定安全系数。

强度折减有限元法介绍

强度折减有限元法基本原理

在外荷载保持不变的情况下，将路基土体的实际强度指标逐渐折减，直至达到边坡失稳临界状态，此时对应的强度折减系数即为边坡安全系数。强度折减法与工程中常用的安全系数法实质上是一致的，只不过前者是假定外荷载保持一定，将材料强度降低一定倍数，而后者是假定材料强度保持一定，把荷载提高一定倍数。

强度折减有限元法基本原理是将土体强度指标c、φ同时除以一个折减系数F得到一组新的c＇、φ＇，如式（1）、（2）所示，然后作为新的材料参数带入有限元进行试算，当边坡土体符合给定的临界破坏判定条件时，对应的F就被称为边坡的最小安全系数[2]。计算中土体的弹性模量E、泊松比μ假设为定值，不随c、φ的改变而变化。

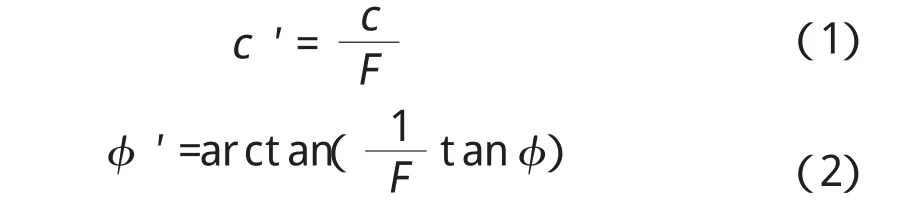
强度折减有限元法边坡失稳判定条件

强度折减有限元法分析边坡稳定性的失稳判定条件有3种[4]，即以特征部位的位移突变为失稳判据，以有限元迭代求解过程的不收敛为失稳判据和以塑性区的贯通为失稳判据。

边坡的整体失稳发生在强度软弱带或应力集中区，该部位土体单元将产生不同程度不可恢复的塑性变形，若发生塑性变形软弱带或应力集中区相互贯通，则表明边坡土体将在相互贯通的剪切破坏面发生整体失稳。因此，塑性应变的大小能够从本质上描述土体的屈服或破坏发展过程，采用从坡脚到坡顶贯通并且出现某一幅值的总等效塑性应变区来判定边坡的整体失稳破坏是比较合理的。

因此，本文将强度折减概念与弹塑性有限元分析及有限元后处理的实时显示相结合，根据塑性区的范围及其连通状态确定潜在滑动面及其对应的安全系数，以此评价边坡的稳定性。

路基边坡稳定性分析实例

物理模型

某山区二级公路路基宽12 m、高8 m，坡度为1∶1.5。模型范围为右边界至坡脚的距离为1.5H（H为边坡高度），坡顶部至底部边界的距离为2H。考虑到结构的对称性，取1/2模型进行分析，见图1。

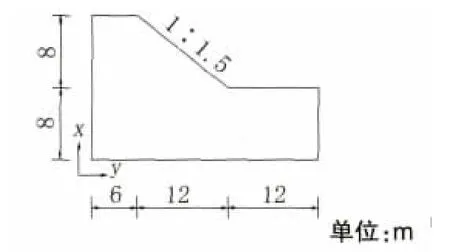
图1 路基边坡模型

材料参数

计算模型为均质材料，土体的物理力学性质参数见表1。

表1 土体物理力学性质参数

有限元模型

按照平面应变问题处理，左边边界对称约束，右边边界水平约束，下部边界固定约束，上部边界和边坡为自由边界。土体采用Mohr Coul omb弹塑性模型。

有限元分析结果

图2为折减系数F分别取1.40、1.50和1.57时边坡的等效塑性应变云图。

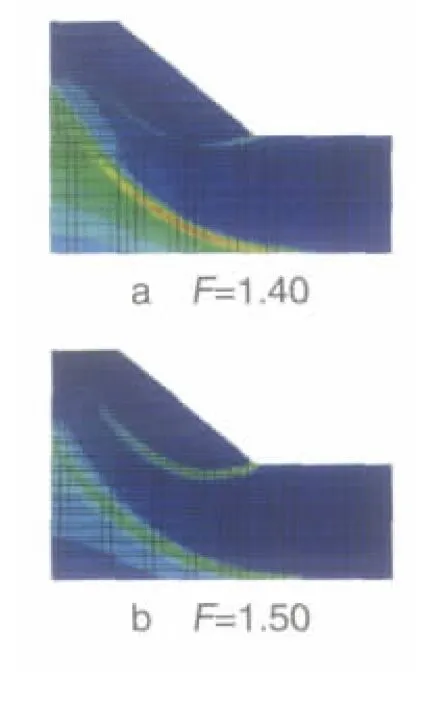
图2 不同折减系数F对应的边坡等效塑性应变云图

计算表明，当折减系数F＞1.58时，计算不收敛，因此，该边坡的稳定系数为1.57，对应的塑性区从坡脚到坡顶贯通。

路基高度和边坡坡度对安全系数的影响

路基边坡的稳定性除了与路基土体的性质有关之外，还与路基断面的几何形状和尺寸有关。本文应用强度折减有限元法分析不同路基高度和坡度对稳定性的影响并与瑞典条分法和毕肖普法进行了对比分析。

图3为3种方法计算的边坡安全系数随路基高度的变化情况（对应的路基坡度均为1∶1.5）。图4为3种方法计算的边坡安全系数随路基坡度的变化情况（对应的路基高度均为8 m）。

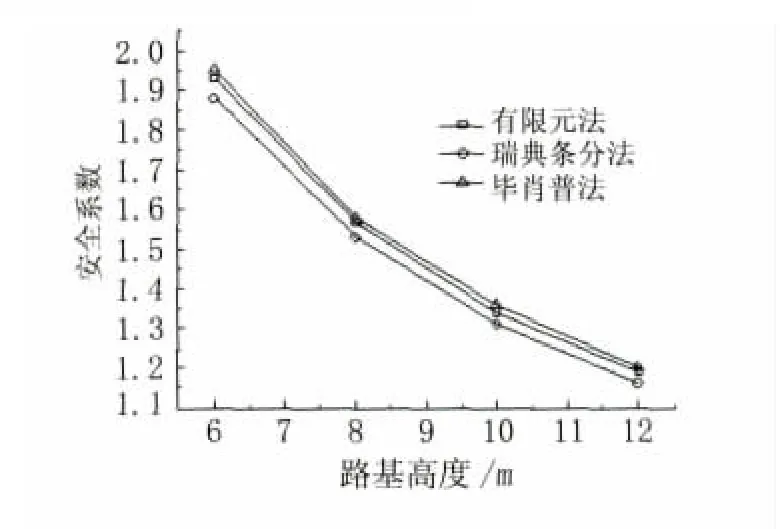
图3 安全系数随路基高度的变化

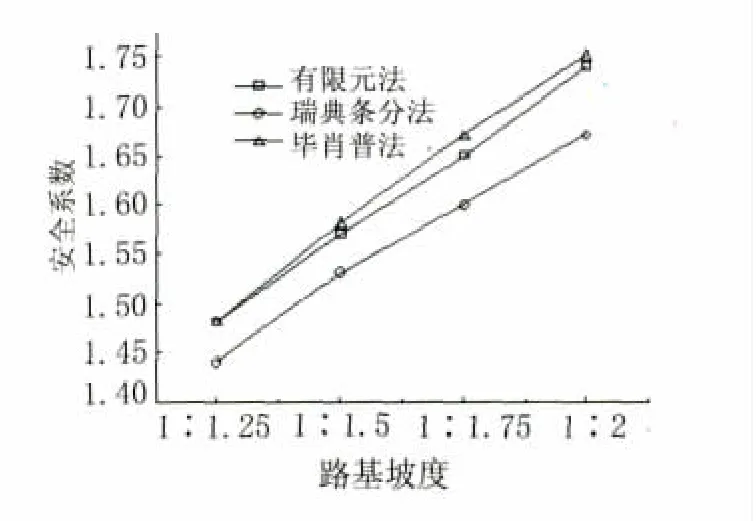
图4 安全系数随路基坡度的变化

图3和图4表明，在相同坡度下，安全系数随着路基高度的增大而减小，而在相同高度下，安全系数随着路基坡度的变缓而增大，强度折减有限元法与极限平衡法计算的安全系数较为一致，其差异在于极限平衡法求解的安全系数是基于条块间力假设的解析解，强度折减法求解的安全系数则为基于应力应变分析的近似解，两类方法基于的理论基础不同，失稳判定标准也不同，因而计算结果之间存在一定差异是合理的。

结论

（1）阐述了强度折减有限元法分析路基边坡稳定性的基本原理并应用该方法进行了路基边坡的实例计算，表明该方法可以动态显示土体不同强度折减系数下广义塑性应变和塑性区的开展情况，可以有效地预测边坡潜在滑裂面的位置和评价边坡的稳定性。

（2）分别应用强度折减有限元法、瑞典条分法和毕肖普法分析了不同路基高度和坡度对边坡稳定性的影响，所得的安全系数较一致，其合理差异在于其基于的理论基础和失稳判定标准不同。

[1]Zienkiewicz O C,Humpheson C and Lewis R W.Associat ed and Non-Associat ed Visco-P-l asticit y and Pl ast icity in Soi l Mechanics[J].G-eot echnique,1975,25（4）：671-689.

[2]张鲁渝,郑颖人,赵尚毅,等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报,2003,（1）：21-27.

[3]Gr if f it hs DV and Lane P A.Sl ope Stabi l it y Anal ysis by Finit e El ements[J].Geotechnique,1999,49(3):387-403.

[4]栾茂田,武亚军,年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报,2003,23（3）:1-8.