承台大体积混凝土施工水化热分析

2010-07-24周恒武闫燕红孙运国

天津建设科技 2010年3期

□文/周恒武闫燕红孙运国

概况

工程概况

南仓斜拉桥是天津市快速路南仓道铁东路互通立交的重点工程，跨径组成为2×150 m，结构形式为独塔4索面预应力混凝土斜拉桥。主塔承台为钢筋混凝土结构，采用强度等级为C30混凝土，承台平面尺寸为53.0 m×25.5 m，厚5.5 m。承台下基础为50根直径2.0 m的钻孔灌注桩。

承台混凝土5.5 m厚采用一次性分层浇注完成，全部承台浇注用时48 h。承台开挖采用钢板桩围护支撑辅助施工，承台浇注模板采用竹胶板模板。

冷却管布置

承台混凝土浇注中在承台内布设4层冷却水管来降低水化热温度，冷却水管采用钢管，外径为30 mm、壁厚2.5 mm。冷却水管在距承台顶面1.25、2.25、3.25和4.25 m4个断面布设，竖向具体布置位置见图1。

图1 冷却水管竖向布置

温度测点布置

在承台施工过程中，承台内部布设29个温度传感器测量承台内部水化热温度变化值。根据承台的对称性，选择承台的1/4角布置传感器进行水化热温度检测。承台内竖向选择3个断面，每个断面布设8个传感器，共计24个，承台中心沿竖向布设5个传感器检测承台中心的水化热温度变化值。承台水化热温度测量传感布置见图2和图3。

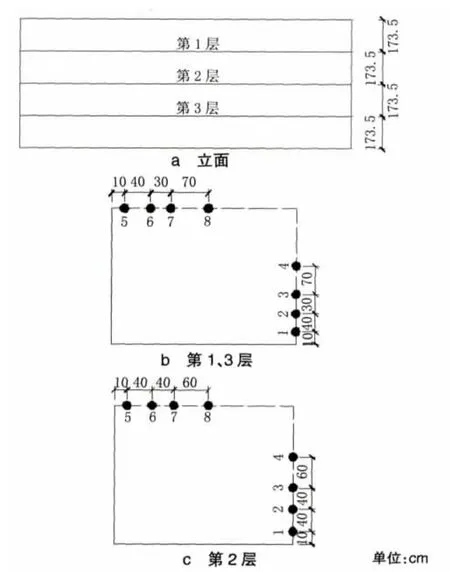
图2 承台1/4角温度测点布置

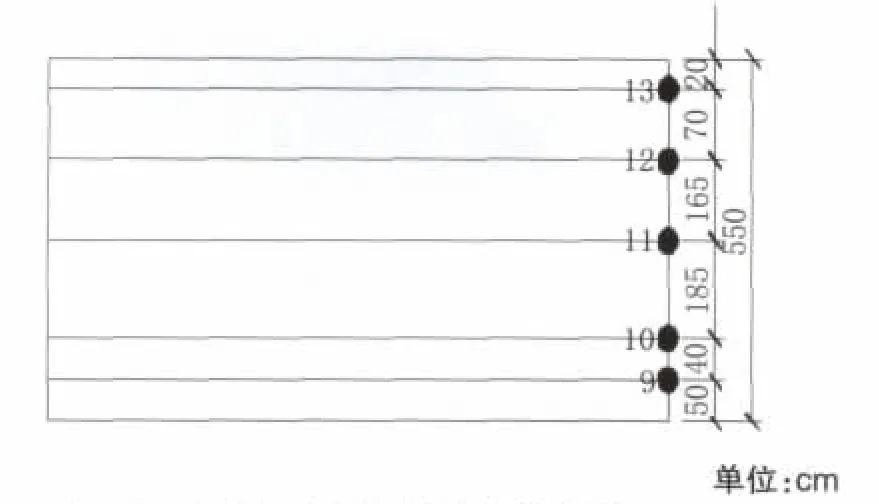
图3 承台中心温度测点布置立面

测温仪器

测温监测传感器采用光纤光栅传感器，光纤光栅传感器具有抗电磁干扰、高灵敏度、耐温性好、耐腐蚀、尺寸小等优点。当光纤光栅所处环境的温度、应力、应变或其他物理量发生变化时，光栅的周期或纤芯折射率发生变化，从而使反射光的波长发生变化，通过测量反射光波长的变化来获得待测物理量的数据。

温度场计算有限元原理

三维热传导平衡方程及热源

混凝土浇注完成后，在混凝土水化热作用下混凝土内部不停的施放出热量，混凝土的水化热过程可以看成内部有热源的连续均匀介质瞬态温度场，瞬态温度场的计算实质是求解三维热传导方程在特定的边界条件和初始条件下的求解，三维热传导方程为

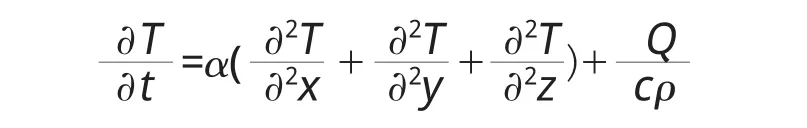
式中：α为导温系数，α＝λ/cρ（m2/h）；λ为导热系数，W/（m·K）；Q为单位时间内单位体积混凝土发出的热量，J/（m3·h）；c为混凝土的比热，J/（kg·K）；t为时间，d；ρ为混凝土密度，kg/m3；T为瞬态温度，K。

混凝土水化热过程发生的热量通过热源函数及绝热温升来模拟，单位时间、单位体积的内部发热量为

式中：K为绝热最高上升温度，℃；α为反应速度系数；t为时间，d。

绝热温度上升式为

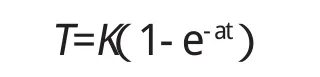
通过初始条件及边界条件来确定热传导方程的解。

热传导方程的初始条件及边界条件

初始条件即混凝土结构的初始温度状态，一般选择在混凝土结构整体温度分布比较均匀的时刻，初始条件为在初始瞬时物体内部的温度分布规律，有以下2种情况。

（1）t=0时，初始温度均是坐标（x,y,z）的已知函数，即

（2）t=0时，初始温度分布是常数，即

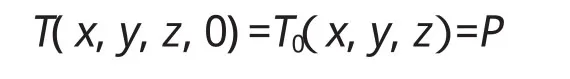
边界条件为混凝土表面与周围环紧介质之间温度相互传递的规律。有以下四类边界条件。

第一类边界条件。混凝土表面温度T是时间的已知函数，即

混凝土与水接触的表面温度等于已知的水温，属于这类边界条件。

第二类边界条件。混凝土表面的热流量是时间的已知函数，即

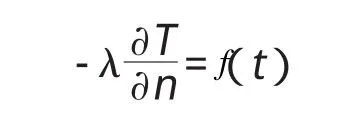
式中：n为外表面法线方向。

若表面为绝热的，则有

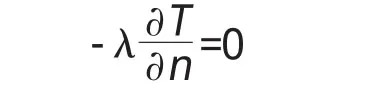
第三类边界条件。当混凝土与空气接触时，假定经过混凝土表面的热量与混凝土表面温度T与Tα气温之差成正比，即

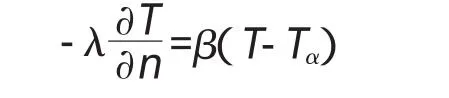
式中：λ为导热系数，W/（m·K）；β为表面放热系数，W/（m2·K）；n为表面外法线方向。

第三类边界条件表示了固体与流体（空气）接触时的传热条件。

第四类边界条件。当2种不同固体接触时，如果接触良好，则在接触面上温度和热流量都是连续的，边界条件为

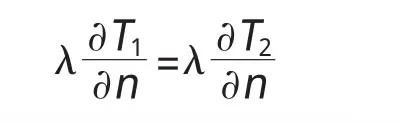
式中：T1、T2分别为2种不同固体接触面上的温度，℃；λ1、λ2分别为 2种不同固体的导热系数，W/（m·K）。

在承台与地基接触面上采用第四类边界条件。

冷管

冷管是把管道埋设在混凝土结构内，通过循环管道内的低温流体进行热交换，来降低水化热引起的温度上升。流体与管道之间的热流量qconv按下式计算

式中：hp为管道的流水对流系数，J/（m2·h·K）；As为管道的表面积，m2；Ts、Tm分别为管道表面和冷却水的温度，K；Ts,j、Ts,o分别为流入位置和流出位置的管道表面温度，K；Tm,j、Tm,o分别为流入和流出位置的冷却水的温度，K。

有限元分析

结合工程的实际情况，由于承台的对称性，取承台的1/4进行计算分析，模型主体由2部分结构组成，分别为地基和承台混凝土。地基模拟成具有一定比热和导热率的结构，水化热过程混凝土的热量可以传给地基，未考虑桩基的影响；承台的侧面有钢模板，承台顶面直接与大气接触，考虑两者的不同，承台侧面和顶面取不同的对流系数；冷却管的位置按实际位置进行模拟，流量及温度取实测值的平均值；承台及地基采用8节点的实体单元模拟。

材料参数

承台混凝土中的水泥取用普通硅酸盐水泥，水泥用量为210 kg/m3，计算中承台混凝土材料比热值取用1.05 kJ/（kg·K）、热传导率取用 9.66 kJ/(m·h·K)。承台及地基材料参数见表1。

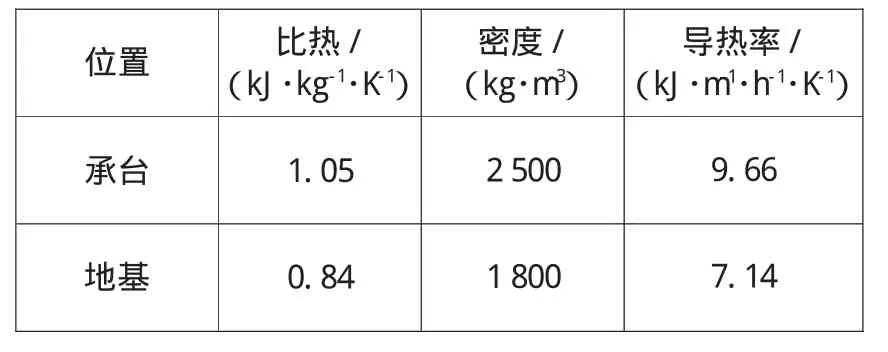
表1 承台及基地的材料参数

冷却管参数的选取

通过水的循环流动来降低混凝土内部的水化热温度。承台内的4层冷却管的热特性参数见表2。

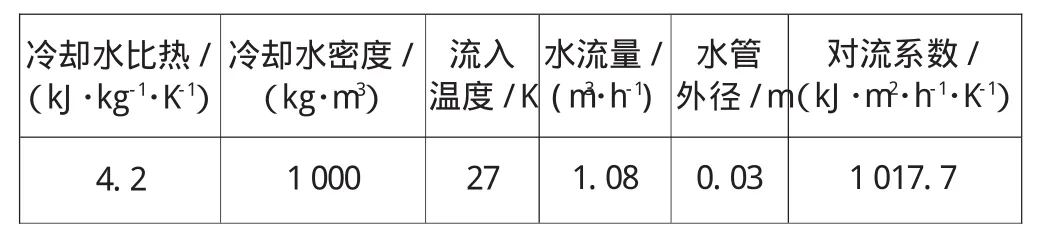
表2 冷却管的热特性系数

模型的建立及边界条件的选取

施工时承台一次性分层浇注完成，每小层厚0.3 m，全部承台高5.5 m，浇注用时48 h。混凝土入仓温度为20.3～32℃，冷却水管进水温度为23～29℃。

由于承台具有对称性，取1/4承台进行建模分析，缩短计算时间。计算模型网格划分图见图4。

图4 模型网格

计算承台温度时，取下述2种边界条件。

（1）模型地基土体边界温度为土壤恒定温度，按第一类边界条件处理，地基土体恒定温度取25℃。

（2）承台与模板及空气接触面按第三类边界条件处理，环境温度取大气平均温度28℃，混凝土表面与大气的对流系数取 154.33 J/(m2·h·K)。

水化热温度结果分析

理论计算承台水化热温度场特征

全部承台混凝土浇注完成40 h后,承台内部温度达到最高69.95℃，由于承台边缘温度降温较快，中部散热慢，承台中心温度较高，边缘温度较低。

实测值与理论计算值比较分析

承台内共计布设29个测温传感器，选择承台的1/4进行布设，在监测承台水化热温度变化的同时，对环境温度、混凝土入仓温度及冷却水温度等进行了监测。取承台东侧第2层（1#～4#）传感器测试温度及承台中心11#传感器测试温度进行比较分析。具体温度的比较见图5和图6。

图5 承台东侧第2层温度测试值与理论值比较

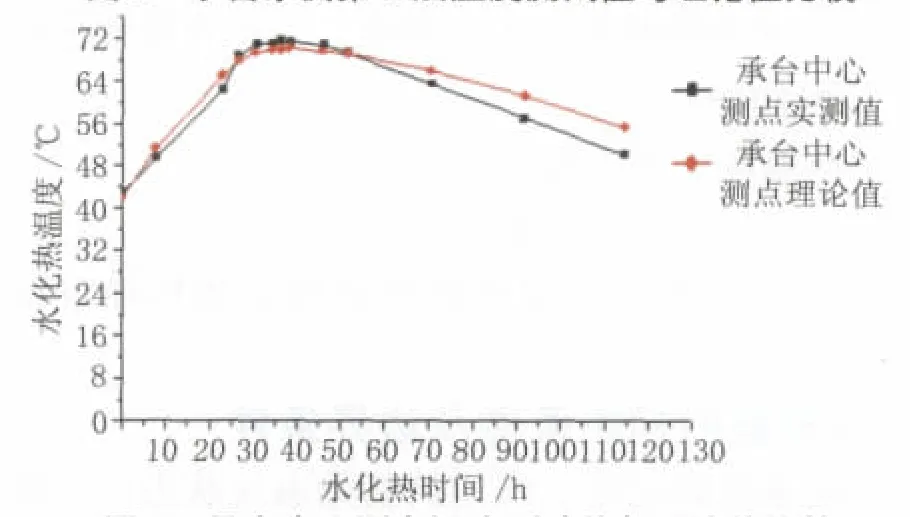
图6 承台中心测点温度测试值与理论值比较

从图5和图6可以看出，计算结果与实测结果是比较接近的，两者差值最大值为5.3℃，出现在承台中心测点。在最高温度区域，曲线基本吻合，理论值较实测值偏低1.2℃，相差不大，可以满足工程需要。在后期时，实测温度下降较快，而理论值下降较慢，这是因为在实际施工过程中，由于承台内温度较高，加快了冷却水的流量，使得承台内实际温度得到了较快的下降，而理论计算过程中整个过程只能设定一个固定的冷却水流量，承台表面在混凝土浇注完成后通过洒水养护，对承台温度降低一定的作用，计算过程未模仿洒水，这是造成后期温度差异的主要原因。

理论计算能较好地计算出结构出现最高温度的时间段和区域。所以在承台大体积混凝土浇注前，进行水化热温度的计算分析是非常必要的，可以预知承台内最高温度出现的时间及位置，从而采用相应的措施予以控制。但是，在实际混凝土搅拌及浇注过程中有很多因素是不定的，理论和实际会有一定的差异，对混凝土内的温度进行检测是必要的。