内置钢箱－混凝土连续组合梁受力性能试验

解恒燕，郑文忠

(1.哈尔滨工业大学 土木工程学院，哈尔滨 150090，xiehy555@163.com;2.黑龙江八一农垦大学工程学院，黑龙江大庆 163319)

内置钢箱－混凝土连续组合梁受力性能试验

解恒燕1，2，郑文忠1

(1.哈尔滨工业大学 土木工程学院，哈尔滨 150090，xiehy555@163.com;2.黑龙江八一农垦大学工程学院，黑龙江大庆 163319)

为研究超静定内置钢箱－混凝土组合梁的塑性设计方法，进行了4根两跨内置钢箱－混凝土连续组合梁试验，获得了试验梁裂缝分布与开展、变形发展、破坏特征及塑性内力重分布等方面的试验结果.通过分析，给出了内置钢箱－混凝土连续组合梁等效塑性铰区长度计算公式，提出了以支座控制截面弯矩弹性计算值与组合梁正截面破坏时钢箱所承担弯矩之差为调幅对象、以相对塑性转角为自变量的弯矩调幅设计方法.

内置钢箱－混凝土连续组合梁;受力性能;内力重分布;等效塑性铰区长度;弯矩调幅

内置钢箱－混凝土组合梁既可用于常规新建工程，也可用于既有房屋的套建增层改造，还可用于巨型框架的建造.它是指采用槽钢或钢板焊接成钢箱，然后在钢箱外围绑扎钢筋骨架并浇筑混凝土而形成的组合梁.以往人们对型钢混凝土组合梁的研究多集中在内置H型钢－混凝土组合梁上，且多为简支梁［1－5］，实际工程中常为超静定梁，而超静定内置型钢－混凝土组合梁的塑性性能研究尚未见系统报道.针对这一问题，在完成内置钢箱－混凝土简支组合梁试验的基础上［6］，进行了4根内置钢箱－混凝土连续组合梁试验，探索了内置钢箱－混凝土连续组合受力性能与塑性设计方法.

1 试验

1.1 试验梁设计与制作

共设计制作了3根内置钢箱－混凝土连续组合梁及1根内置钢箱－预应力混凝土连续组合梁.试验梁截面尺寸均为b×h=250×400 mm，混凝土采用设计强度等级为C40的自密实混凝土，内置钢箱采用Q235的两根25a槽钢对焊而成，钢箱在截面中均为对称布置.纵筋采用HRB335钢筋，箍筋采用HPB235钢筋.试验梁基本参数如表1所示.以梁L－1为例，中支座及跨中截面配筋如图1所示.

表1 试验梁基本参数

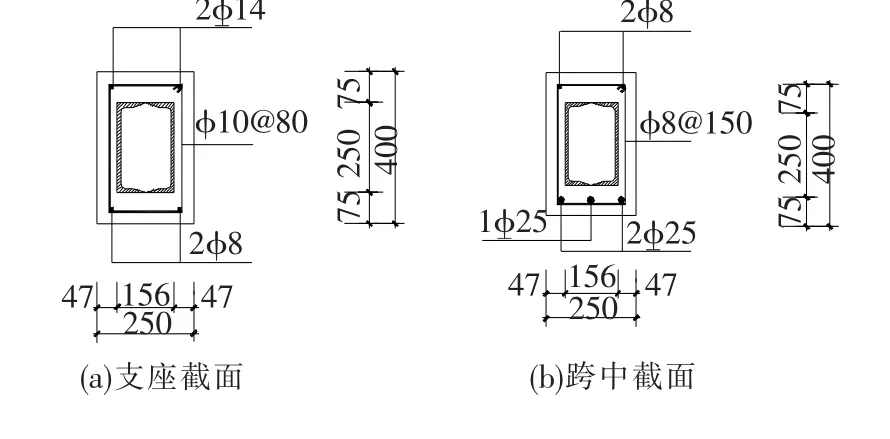
图1 梁L－1截面配筋图(mm)

梁YL的配筋是按照其支座及跨中控制截面承载力分别与梁L－2大致相当来设计的，预应力筋采用两根抗拉强度标准值为fptk=1 860 N/mm2的U5无粘结钢绞线，其在钢箱内部通过，线型如图2所示.预应力筋设计张拉控制应力为σcon=0.75fptk.

图2 梁YL预应力筋线型

1.2 材料性能

试验梁自密实混凝土标准立方体抗压强度、标准棱柱体抗压强度及弹性模量实测值分别为fcu=49.67 N/mm2，fc=39.89 N/mm2，Ec=3.37×104N/mm2.采用文献［7］给出的公式计算得到混凝土的抗拉强度ft=0.21f2/3cu=2.84 N/mm2.采用MTS试验机进行了尺寸为100 mm×100 mm×300 mm的棱柱体试件试验，按照文献［8］附录C给出的混凝土单轴应力－应变关系进行拟合，得到的各参数值为:αa=1. 806，αd=1. 063，ε0=2 193.4 × 10－6，εu/ε0=2.55.其中αa，αd为公式中的系数，ε0为与混凝土应力－应变曲线上峰值应力对应的峰值应变;εu为曲线下降段上应力等于峰值应力一半时的混凝土压应变.试验及拟合得到自密实混凝土单轴受压应力－应变关系见图3.

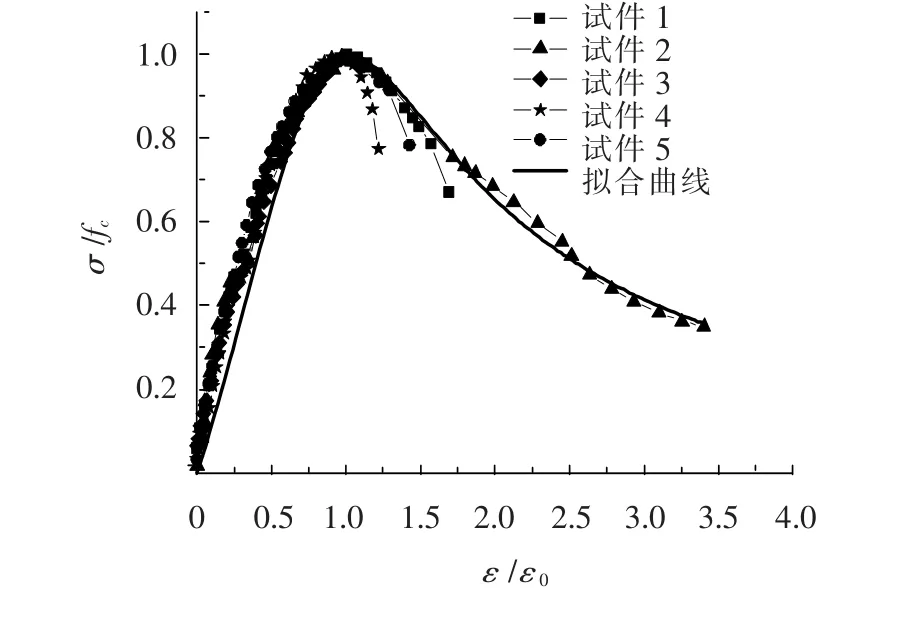
图3 自密实混凝土受压应力－应变关系

钢筋及槽钢的屈服强度fy、极限强度fu及屈服应变εy实测值见表2.

1.3 试验方案

1.3.1 试验装置

试验装置如图4所示.采用液压千斤顶分别在梁两跨中单点对称施加荷载，试验梁中支座为可调铰支座，试验全貌如图5所示.

表2 钢筋及槽钢的力学性能指标

图4 试验装置示意图

图5 试验全貌

1.3.2 测点布置

为测得塑性铰区长度及塑性铰区截面曲率分布，在试验梁中支座两侧各600 mm范围的受拉纵筋及钢箱翼缘上分别均匀密布粘贴了间距为25 mm的电阻应变片.在试验梁中支座控制截面及两跨中控制截面的纵筋及钢箱上粘贴了应变片.

1.4 试验现象

由4根试验梁从开始加荷至破坏的全过程可知该类梁的受力性能具有以下特点:

1)内置钢箱－混凝土连续组合梁中支座塑性铰应以控制截面钢箱受拉翼缘及纵筋二者之一出现屈服作为塑性铰形成的标志，此时对应的曲率为截面屈服曲率.本批试验梁均为钢箱受拉翼缘先达到屈服，此时钢箱受拉翼缘应变为1 200×10－6.加荷至支座控制截面压区边缘混凝土达到极限压应变(εcu=3 200×10－6)后仍可继续加荷，这是由于支座控制截面所承担的弯矩虽有一定幅度的减小，但跨中控制截面所承担的弯矩在不断增大，这使得总静力弯矩增大.

2)内置钢箱－预应力混凝土连续组合梁开裂荷载比其他试验梁开裂荷载高.

3)由于外围钢筋混凝土未受到钢箱约束，当压区边缘混凝土被压碎时，钢箱两侧的混凝土也迅速破裂.

以梁L－3为例，图6、7分别为梁跨中、中支座区域混凝土的破坏情况，图8为梁裂缝分布图.

图6 梁L－3跨中混凝土压碎区

图7 梁L－3中支座区域的破坏

图8 梁L－3裂缝分布图

内置钢箱－混凝土连续组合梁以任一跨出现变形增大而荷载开始减小的现象作为破坏标志，此为破坏标志Ⅰ，该破坏标志是真实的破坏标志.而实际工程中，多以一个控制截面受压边缘混凝土达到极限压应变为连续梁的破坏标志，此为破坏标志Ⅱ，这一标志也是开展连续梁塑性设计方法研究的基点.

1.5 试验结果

1.5.1 跨中变形

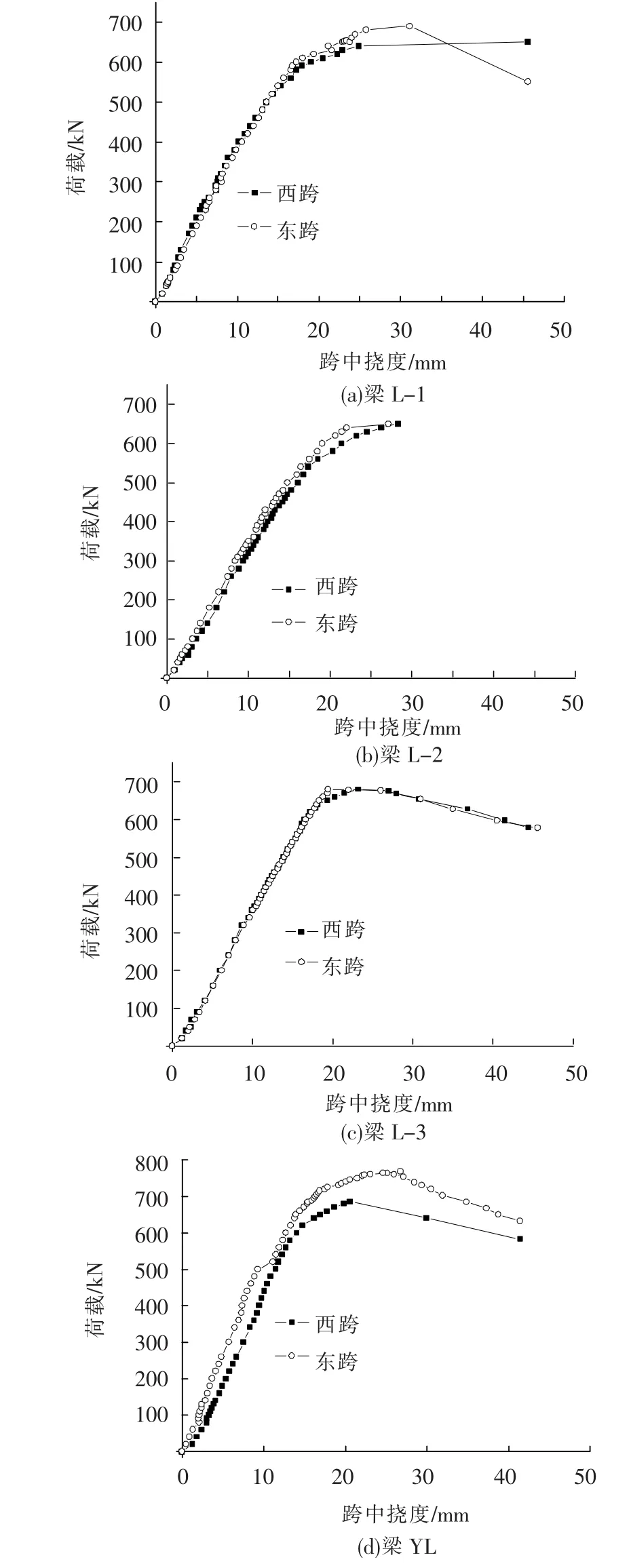
图9 试验梁荷载－跨中挠度曲线

4根试验梁荷载－跨中挠度曲线如图12所示，曲线的终点对应于极限荷载的85%.(梁L－2加载后期边支座辊轴飞出，故未得到变形曲线下降段.)

由图9可知该类梁荷载－跨中挠度曲线特点:

1)试验梁开裂、钢箱受拉翼缘及受拉纵筋屈服对荷载－挠度曲线走向的影响不大.

2)即使荷载下降明显、变形发展比较大时，梁承载力一直保持相当的水平.

1.5.2 无粘结筋应力增量

梁YL荷载－预应力筋应力增量曲线如图10所示.试验梁开裂前预应力筋应力几乎没有增加，继中支座附近混凝土开裂后，预应力筋应力稳步增长，在中支座控制截面钢箱受拉翼缘进入屈服后，预应力筋应力增长速度加快，在跨中受拉纵筋屈服后，预应力筋应力急剧增大，直到构件达到破坏.

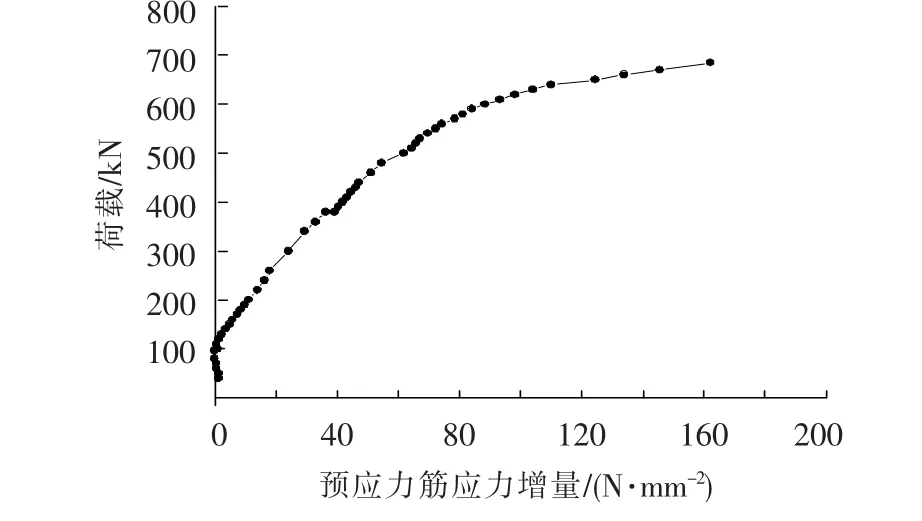
图10 梁YL荷载－预应力筋应力增量曲线

2 连续组合梁塑性设计方法

2.1 内力重分布现象

4根试验梁加载后均为中支座先形成塑性铰，跨中后形成塑性铰，最后形成机动体系而破坏.内置钢箱－混凝土组合梁塑性铰的转动能力介于钢梁与钢筋混凝土梁之间.试验梁跨中与中支及控制截面弯矩实测值与弹性计算值的对比如图11所示.

由图11可知，在从开始加荷至中支座区混凝土开裂前，试验梁的控制截面弯矩实测值与弹性计算值基本吻合;继续加荷至中支座控制截面钢箱受拉翼缘屈服，二值逐渐出现偏差，中支座弯矩实测值逐渐小于弹性计算值，跨中弯矩实测值逐渐大于弹性计算值;在继续加荷至试验梁破坏的过程中，这种差距越来越明显，表明内置钢箱－混凝土连续组合梁出现了明显的塑性内力重分布.

2.2 塑性铰性能

对于本次试验，以中支座控制截面钢箱受拉翼缘应变达到1 200×10－6时的截面曲率作为屈服曲率.以中支座压区边缘混凝土达到极限压应变εcu=3200×10－6时的截面曲率作为极限曲率.本次试验钢箱受拉翼缘先达到屈服，而在实际工程中许多情况下是受拉纵筋先屈服，在分析该类梁塑性性能时，将以受拉纵筋屈服作为出铰标志的塑性铰性能及弯矩调幅方法一并给出.

图11 试验梁跨中与中支座控制截面弯矩实测值与弹性计算值的对比

2.2.1 等效塑性铰区长度的确定

按与实际塑性铰区范围内非弹性曲率分布曲线所围面积相等(保证塑性转角相等)的原则，将非弹性曲率等效为矩形分布后，可确定试验梁中支座两侧的等效塑性铰区长度.以钢箱受拉翼缘屈服为出铰标志的试验梁实测曲率分布及等效矩形如图12所示.图中横坐标为距中支座控制截面的距离，纵坐标起点为钢箱受拉翼缘屈服时刻的截面曲率.以受拉纵筋屈服为出铰标志的试验梁实测曲率分布及等效矩形如图13所示，图中纵坐标起点为受拉纵筋屈服时刻的截面曲率.

图12 以钢箱受拉翼缘屈服为出铰标志的试验梁实测曲率分布及等效矩形

图13 以钢箱受拉翼缘屈服为出铰标志的试验梁实测曲率分布及等效矩形

得到试验梁屈服曲率φy与极限曲率φu后，根据θp=(φu－φy)Lp，可确定试验梁中支座一侧塑性转角θp.各试验梁以钢箱受拉翼缘屈服为出铰标志的中支座塑性铰基本参数(两侧塑性铰基本参数平均值)如表3所示，以受拉纵筋屈服为出铰标志的塑性铰基本参数如表4所示.

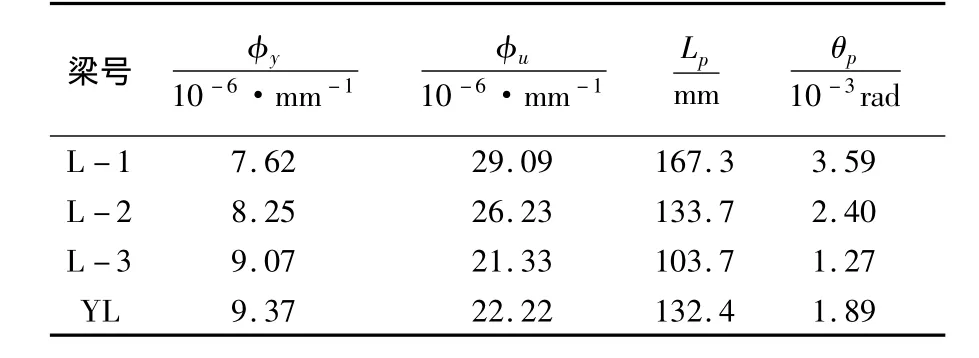
表3 以钢箱受拉翼缘屈服为出铰标志的中支座塑性铰基本参数实测值

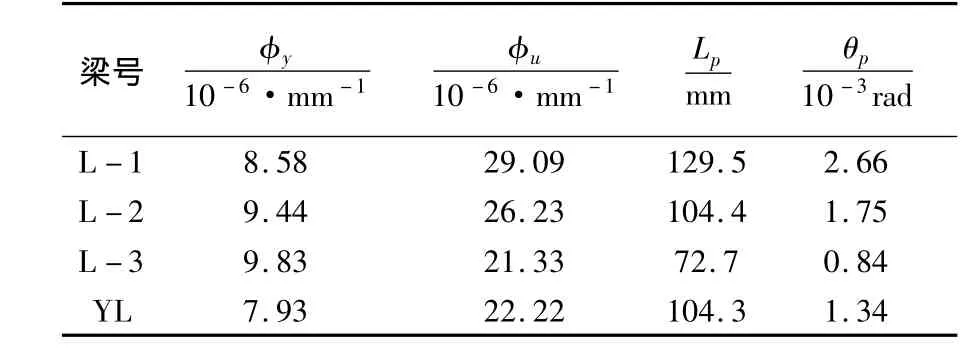
表4 以受拉纵筋屈服为出铰标志的中支座塑性铰基本参数实测值

2.2.2 等效塑性铰区长度计算公式

试验梁以钢箱受拉翼缘屈服为出铰标志的等效塑性铰区长度平均值为0.404 h0，等效塑性铰区长度为

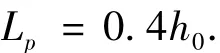
试验梁以受拉纵筋屈服为出铰标志的等效塑性铰区长度平均值为0.309 h0，等效塑性铰区长度为

这里h0为受拉纵筋及钢箱受拉翼缘合力点至混凝土受压边缘的距离，对于内置钢箱－预应力混凝土连续组合梁，h0的计算考虑预应力筋应力增量部分.

2.3 弯矩调幅分析

2.3.1 分析思路

试验梁在中支座控制截面钢箱受拉翼缘屈服、受拉纵筋屈服及试验梁破坏等标志状态下中支座控制截面弯矩弹性计算值与实测值及其比较如表5所示.

由表5可知，随着中支座受拉纵筋配置的增加，试验梁内力重分布程度越来越小，其弯矩调幅幅度也越来越小.

表5 试验梁在各标志状态中支座控制截面弯矩弹性计算值与实测值及其比较 kN·m

一般房屋楼盖中的连续次梁、连续板是允许按塑性设计的.通常超静定钢梁可发生充分的塑性内力重分布，可按截面完全达到塑性进行计算.众多学者对钢筋混凝土连续梁板的塑性设计进行了系统的研究，其弯矩调幅系数有表可查［9－10］.超静定型钢－混凝土组合梁的塑性性能研究未见系统报道.我们认为在研究内置钢箱－混凝土连续组合梁的塑性内力重分布时，可先根据平截面假定计算出支座控制截面达到正截面承载能力极限状态时内置钢箱承担的弯矩Ma，然后再计算出在外荷载作用下支座控制截面弹性弯矩计算值Mload，最后计算出弹性弯矩计算值与钢箱所承担弯矩的差值ΔM=Mload－Ma，最后建立以内置钢箱－混凝土连续组合梁支座相对塑性转角θp/h0为自变量、以ΔM为调幅对象的调幅系数β的计算公式.

2.3.2 弯矩调幅系数计算公式

4根试验梁达到承载能力极限状态时梁实测的Ma、ΔM及ΔM的调幅系数β如表6所示.

以钢箱受拉翼缘屈服为出铰标志，以相对塑性转角θp/h0为横坐标，以ΔM的调幅系数β为纵坐标，可得到4根试验梁β与θp/h0试验点分布，如图14所示.

弯矩调幅系数β的计算公式为

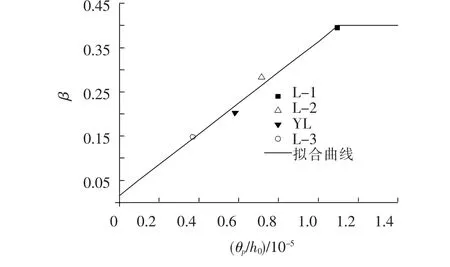
图14 以钢箱受拉翼缘屈服为出铰标志的((θp/h0)，β)试验点分布及拟合曲线

同样可得到以受拉纵筋屈服为出铰标志的4根试验梁β与θp/h0试验点分布，如图15所示.

图15 以受拉纵筋屈服为出铰标志的((θp/h0)，β)试验点分布及拟合曲线

弯矩调幅系数β的计算公式为

在计算得到弯矩调幅系数后，可求得内置钢箱－混凝土连续组合梁中支座控制截面的调幅后弯矩值:

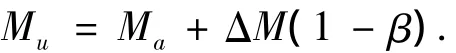
3 结语

4根内置钢箱－混凝土连续组合梁试验研究表明:这类梁的等效塑性铰区长度计算公式及以支座控制截面弯矩弹性计算值与组合梁正截面破坏时钢箱所承担弯矩之差为调幅对象、以相对塑性转角为自变量的弯矩调幅计算公式可按照文中给出的相应公式进行计算.

［1］日本建築學會.铁骨铁筋コンクリ——ト構造計算規準同解説［S］.日本国东京都:丸善株式会社，1987.

［2］CHICOINE T，MASSICOTTE B，TREMBLAY R.Longterm behavior and strength of partially encased composite columns made with built-up steel shapes［J］.Journal of Structural Engineering， 2003，129(2):141－150.

［3］XIAO Hui.Experimental study on ultimate flexural capacity of steel encased concrete composite beams［J］.Journal of Southeast University， 2005，21(2):191 －196.

［4］EN 1994-1-1:2004.Eurocode No.4.Design of Composite Steel and Concrete Structures［S］.Part 1.1:General Rules and Rules for Building.(English version)Brussels:European Committee for Standardization，2004.

［5］ASTANEH-ASL A.Behavior and Design of Steel and Composite Structures Including Seismic Effects［M］.Berkeley:University of California，2004.

［6］解恒燕，郑文忠.内置钢箱－混凝土简支组合梁受力性能研究［J］.哈尔滨工业大学学报， 2009，41(2):37－42.

［7］罗素蓉，郑建岚，王国杰，等.自密实高性能混凝土结构的研究与应用［J］.土木工程学报， 2005，38(4):46－52.

［8］中华人民共和国建设部.GB50010－2002混凝土结构设计规范［S］.北京:中国建筑工业出版社，2002.

［9］郑文忠，李和平，王英.超静定预应力混凝土结构塑性设计［M］.哈尔滨:哈尔滨工业大学出版社，2002:3.

［10］CEB欧洲国际混凝土委员会.1990CEB－FIP模式规范［S］.北京:中国建筑科学研究院结构所规范室译，1991.

Experimental research on mechanical behavior of continuous encased steel box concrete beam

XIE Heng-yan1，2，ZHENG Wen-zhong1

(1.School of Civil Engineering，Harbin Institute of Technology，Harbin 150090，China，xiehy555@163.com;2.School of Engineering，Heilongjiang Bayi Agricultural University，Daqing 163319，China)

In order to investigate the plastic design method of indeterminate encased steel box concrete beam(ESBCB)，4 two－span continuous ESBCBs are tested，and then the distribution and growth of crack，deformation，failure characteristics and redistribution of plastic internal force are obtained.The calculation formula of the length of equivalent plastic hinge of ESBCBs is presented.A design method for moment modification is put forward，in which the object of moment modification is the difference between the elastic calculated moment of critical section at intermediate support and the moment subjected to the steel box when the composite beam reaching the limit state of bending capacity，and the variable is the relative plastic rotation.

continuous encased steel box concrete beam(ESBCB);mechanical behavior;redistribution of internal force;length of equivalent plastic hinge;moment modification

TU398+.2

A

0367－6234(2010)02－0186－07

2009－02－21.

教育部新世纪优秀人才支持计划资助项目(教科司［2005］290号);黑龙江省科技攻关资助项目(GC04A609).

解恒燕(1973—)，女，博士;

郑文忠(1965—)，男，教授，博士生导师.

(编辑 赵丽莹)