潮汐数据的达尔文分析与调和分析的对比研究
2010-07-16牛桂芝裴文斌
牛桂芝,裴文斌
(交通部天津水运工程科学研究所,天津300456)
海洋潮汐变化是一种复杂的周期性变化,在航海、海上工程建设和海洋科学研究等活动中起重要作用,而潮汐数据分析是提取潮汐变化规律的方法,它的准确与否将直接影响人类在海上的各项实践活动。
1 方法原理对比分析
1.1 达尔文分析法原理
达尔文分析法的基本原理是,依据不同分潮具有不同的角速率,将潮汐变化划分为不同分潮系的振动,而后以某一分潮系的周期为准,将其不同周期的同相潮位进行叠加,以消除异系分潮的影响,得到较为纯净的该分潮系的振动,并在此基础上,通过三角函数等数学推导方法进一步获得分潮系内某一特定分潮的振幅和迟角。划分的分潮系包括M、S、O、K、N和MS分潮系。
达尔文分析在理论上主要存在以下几点不足。
(1)不同周期的同相潮位叠加时,对于除S2外的分潮,每个周期的同相潮位均不能保证有实测数据,对此达尔文法近似地取整点或内插的半点时刻数据代替这些没有实测数据的同相潮位,这种近似替代会由于非天文潮位(余水位)的大小、海底地形、观测的天文日期和当地潮汐性质的影响,给对分析结果带来大小不同的误差。
(2)对同相潮位进行叠加并选择适当的天数,能够有效削弱异系分潮的影响,但主要削弱的是与其频率相近的分潮系,对其他系分潮的削弱效果可能较差,尤其在数据时间长度较短、所求分潮能量较弱的情况下,残留的异系分潮因素相对较大,会对分析结果造成较大影响。
(3)对于分潮系内次要的Q1、P1和K2分潮,它们分别依附于O1、K1和S2分潮,分析时按照振幅呈特定比例关系、迟角相等的原则进行求解,但这种原则仅对主次分潮间关系进行粗略描述,事实上在不同地点,主次分潮间的差比关系会略有变化,故达尔文法不可避免的会造成主次分潮间相互影响,使得分析结果产生差异。
1.2 调和分析法原理
调和分析法的基本原理是采用较为精确的引潮力展开得到的分潮的纯调和表达式建立潮汐表示模型,通过最小二乘平差原理求解参与模型的分潮的振幅和迟角,求得的参数能够使所有观测时刻的模型值最接近实测水位[1-7]。
按照平差思想,调和分析法所得结果是一种最优的分析结果,理论上能够求得任意分潮的振幅和迟角,但由于观测值和模型不可避免地会存在偏差,故该方法还存在一个分辨率的限制,即观测时间长度越长,所能分离的分潮间的最小频率差越小,反之则越大。目前,对于1 a数据往往采用122个分潮进行建模分析,1个月数据采用11个分潮进行建模,但需要引入P1与K1、K2与S2分潮的差比关系作为限制条件,以满足调和分析的分辨率限制。
1.3 方法的对比分析
经理论分析,调和分析法相对达尔文分析法具有以下优点.
(1)调和分析过程中直接采用实测数据即可完成分析,而不需内插实测数据,故该方法避免了达尔文分析中采用实测值或内插的中间时刻值所造成的误差。
(2)当存在个别或小段缺测数据时,调和分析法结果基本不受影响,但达尔文分析结果却可能产生较大误差,尤其在潮差较大海域,由于潮位内插精度可能较低,达尔文分析结果甚至可能出现错误。
(3)受分辨率限制,调和分析法虽然同样不能完全消除分潮之间的相互影响,但相对于达尔文分析法主要以消除频率相近分潮系为初衷的分析方法,理论上分潮分离的效果应更好。
(4)达尔文分析中Q1、P1和K2分潮是依附于O1、K1和S2分潮进行求解的,而调和分析中P1和K2分潮是依据平衡潮中其与K1和S2分潮的理论关系得到的,Q1分潮则独立运算得到,理论上调和分析法更符合潮汐运动变化的实质,故上述3个次要分潮的分析结果也应更为准确。
(5)当观测数据时间大于1个月时,调和分析法能够分离较多数量的分潮,但达尔文分析法所得到的分潮只能固定为11个分潮,否则需对其计算原理进行重新推证,而当观测数据时间小于半个月时,调和分析法同样适用或仅需做出部分改动[1],但达尔文分析法失效,因此调和分析法相对具有较好的适用性。
2 试验分析结果
2.1 采用的数据和方法
试验数据采用渤海内某长期验潮站实测数据,数据起止时间为2000年1月1日0时~2007年12月31日23时,数据采样间隔1 h,数据总量70 128个,期间无缺测数据。
采用上述实测数据,分别按照以下方法,对达尔文分析法和调和分析法进行对比分析。
(1)将数据划分为以月为单位的96个数据段,分别对各段数据进行达尔文分析和调和分析,比较2种方法分析结果的月变化过程。
(2)以年为单位,分别对8 a的数据进行达尔文分析和调和分析,比较2种方法分析结果的年变化过程。
2.2 月分析结果
经计算统计,2种方法11个分潮的月分析结果的变化过程基本相似,但略有区别,图1给出了K1分潮振幅和迟角的变化情况,2种方法振幅和迟角的平均差异分别为1.1 cm和2.0°,振幅最大差异出现在2001年3月(3.6 cm),迟角最大差异出现在2001年4月(7.4°)。其余分潮的相关统计计算结果见表1,其中由于浅水分潮量级较小,在此并未列出统计结果。
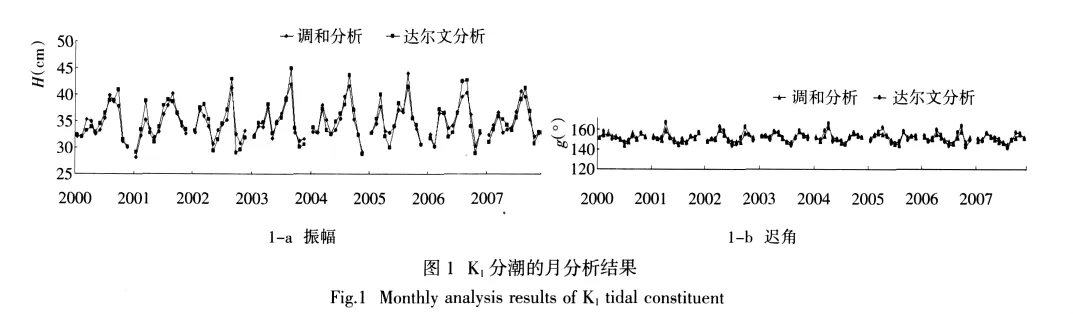
由表1可见,Q1、P1、N2和K2分潮的迟角差异相对其余分潮较大,其原因是达尔文分析认为Q1、P1和K2分潮迟角分别与O1、K1和S2分潮迟角相等,但事实上两者在不同地域是存在差异的,达尔文分析结果在此并不可信;而调和分析是以对应两者的平衡潮理论关系推导的,该理论关系中认为P1与K1、S2与K2迟角之间为一个固定偏差,虽然该理论关系同样存在缺陷,但相对达尔文分析法更接近于实际天文潮变化情况。
N2分潮迟角差异偏大的原因可能是达尔文分析在提取N系分潮时,是以消除M系分潮而选定待分析数据时间长度的,故同为半日潮的S系分潮可能会对N系分潮的提取结果造成一定影响,使得达尔文分析结果中N2分潮出现一定偏差。
表1中M2分潮的振幅和迟角差异均很小,其原因可能是在半日分潮中,M系分潮一般占有较大优势,N系和S系分潮对其造成的影响相对较小,故其分析结果可能较为准确,而日分潮系中O1和K1分潮量级相差不大,故两系分潮相互影响可能较大。
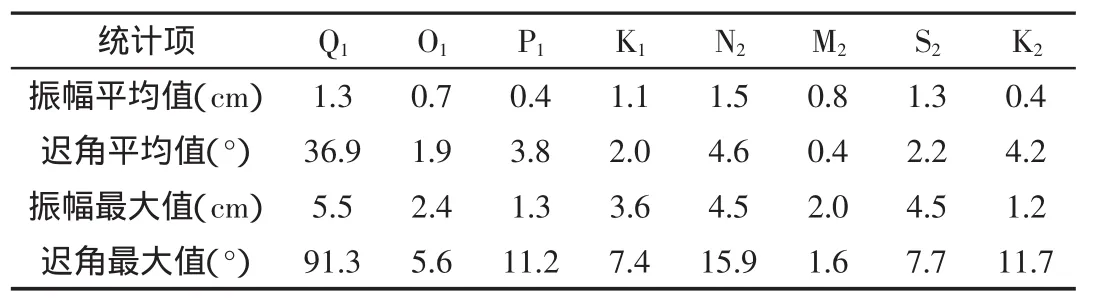
表1 主要分潮差异的统计结果Tab.1 Statistical results of differences between main tidal constituents
2.3 年分析结果
经计算统计,2种方法得到的11个分潮的年分析结果基本相符,但略有差别。本文在此仅给出K1和M22个振幅最大分潮的分析结果(图2和图3)用以分析和说明。
由图2和图3可见,年调和分析结果的稳定性要明显好于达尔文分析,这表明调和分析结果更加接近于稳定不变或变化幅度很小的真实值。为方便分析,本文在此采用统计量C衡量分析结果的稳定性

式中:Xi为潮汐分析所得某一分潮的参数,其中i为第i年所得参数;为该参数8 a分析结果的平均值。按照式(1)统计计算8个主要分潮的统计量,其结果见表2。其中在振幅稳定性方面,2种方法的Q1、P1和K2分潮稳定性相差不大,其余分潮的调和分析法则明显好于达尔文分析法;在迟角稳定性方面,除Q1、P1和K2分潮外,其余分潮的调和分析结果也好于达尔文分析法,而上述3个分潮由于迟角采用O1、K1和S2分潮结果,其本身存在较大偏差,故其稳定性统计量在此不具有说明意义。


表2 主要分潮的稳定性统计Tab.2 Stability of main tidal constituents
3 结论
由以上理论分析和试验验证可知,调和分析法较之达尔文分析法具有较高的精度,并且分析所得结果的稳定性也较强。造成2种方法结果差异的原因主要有以下几点。
(1)对于达尔文分析法,离散的观测数据不能保证每个周期的同相潮位均有实测数据,故在分潮系分离时,该方法较之调和分析法将增加实测潮位内插或不准确所引起的误差。
(2)在分潮系分离时,达尔文分析的原理主要是注重分离频率相近的分潮系,而忽略其余分潮系影响,在数据量较短的情况下,可能会使得分潮系之间存在较大的相互影响,而调和分析法有严密的分辨率限制关系式,该限制使得不同分潮间能够得到有效分离,从而提高分潮分析结果的精度。
(3)达尔文分析中Q1、P1和K2分潮是由O1、K1和S2分潮推算得到,这种推算关系相对调和分析法中引入的分潮差比关系较为粗略,尤其是迟角,采用与主要分潮相等的迟角可能使分析结果产生较大误差。
(4)在数据量较大的情况下(如1 a数据),达尔文分析法由于原理限制,可分离的分潮数目较少,故其余分潮和非天文水位(余水位)可能会对分析结果产生较大的随机影响,影响分析结果精度,并使其稳定性下降,而调和分析能够分离包括数量较多的浅水分潮、长周期分潮等,故精度和稳定性要高于达尔文分析法。
基于上述原因,达尔文分析法虽然在一定时期内被作为一种标准的潮汐方法,但其分析结果精度要低于调和分析法,分析原理也相对粗略,故在条件允许的情况下,建议潮汐分析采用调和分析法。假若缺少相关设备和软件,潮汐分析只能以手工方式进行时,仍可采用计算简易、快捷的达尔文分析法。
[1]方国洪,郑文振,陈宗镛,等.潮汐和潮流的分析和预报[M].北京:海洋出版社,1986.
[2]黄祖珂,黄磊.潮汐原理与计算[M].青岛:中国海洋大学出版社,2005.
[3]裴文斌,牛桂芝,董海军.余水位及潮汐差分方法[J].水道港口,2007,28(6):439-443.PEI W B,NIU G Z,DONG H J.Residual water level and tide difference method[J].Journal of Waterway and Harbor,2007,28(6):439-443.
[4]暴景阳,晁定波,李建成.中国南海 TOPEX/POSEIDON 轨迹交叉点测高数据的潮汐调和分析[J].测绘学报,2000,29(1):17-23.BAO J Y,CHAO D B,LI J C.South China Sea TOPEX/POSEIDON altimeter data tracks crossing the tidal harmonic analysis[J].Journal of Surveying and Mapping,2000,29(1):17-23.
[5]杨东远,牛桂芝.VBA 在 Excel水文数据处理中的应用研究[J].水道港口,2008(3):223-228 .YANG D Y,NIU G Z.VBA in Excel hydrological data processing research[J].Journal of Waterway and Harbor,2008(3):223-228.
[6]裴文斌,牛桂芝.马来西亚达道河口潮汐分析[J].水道港口,1999(3):43-45.PEI W B,NIU G Z.Tidal reach of the Malaysian Road[J].Journal of Waterway and Harbor,1999(3):43-45.
[7]方国洪,郑文振,陈宗镛,等.潮汐和潮流的分析和预报[M].北京:海洋出版社,1986.
