双曲线法在路基沉降变形预测中的应用分析

姬庆峰

(沧州路桥工程公司)

1 前 言

路基沉降变形中采用科学的预测方法处理实测资料,有助于准确地预测沉降,从而使后期施工组织安排达到最优化,具有一定的经济效益。在目前工程中通过实测的成果曲线反算地基最终沉降的方法很多,常用的有双曲线法、指数曲线法、沉降速率法、三点法以及日本的星野法等。这些方法各有优缺点,关键视其与实际情况拟合程度的好坏,选择与实际情况较吻合或者接近的方法。

2 双曲线预测模型及原理

双曲线法是假定下沉平均速率以双曲线形式减少的经验推导法。从填土开始到任意时间 t的沉降量 St可用下式来求得。其推算模式见图 1、图 2。

图 1 双曲线法推算下沉模式图

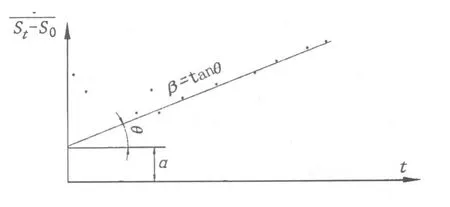
图 2 α、β的求法

式中:t为经过时间;S0为初期沉降量(t=0);St为t时沉降量。

α、β从实测值求得的系数。

将上式变换为直线方程的形式

当 t→∞时,最终沉降量 S∞可用下式求得

荷载经过时间 t后的残余沉降量△S可用下式求得

用此方法推算 t时沉降量,要求实测沉降时间至少在半年以上。

3 路基沉降量预测分析实例

根据某高速公路路基沉降观测的时间以及断面的典型性,同时考虑实测数据的代表性与准确性,选择第五合同段的K 18+500断面(碎石桩处理软基高路堤)进行沉降预测分析。沉降预测数据的时间段为 2006年 4月 5日 ～2008年 1月 28日,满足双曲线模型预测实测沉降时间在半年以上的要求。

3.1 元件的埋设

该断面沉降观测元件的埋设见图 3。已经埋设了三个元件,进行了近两年半的沉降观测,获得了真实有效的数据。

图 3 沉降观测元件埋设示意图

3.2 双曲线拟合曲线方程的确定

以 2005年 4月 5日 ～2007年 1月 28日时间段沉降观测数据,建立曲线拟合方程。确定曲线方程参数 α=0.035 55,β=0.005 32。相应的曲线方程为

曲线拟合的相关系数为 0.95,关联度较大。其拟合曲线见图 5。

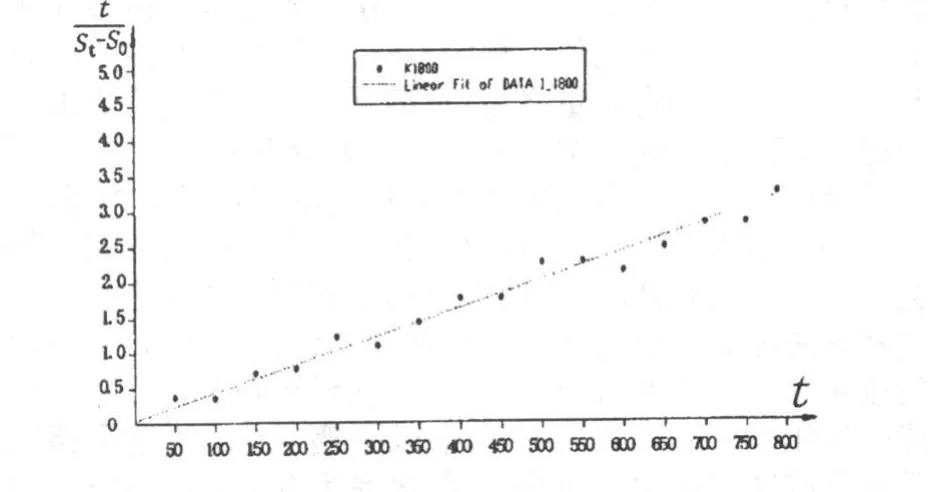
图 5 K 18+500断面沉降预测双曲线拟合计算图

3.3 用前期实测数据预测后期沉降

根据拟合的双曲线方程预测后期一段时间的沉降,并与实测数据进行对比。结果表明,预测取得了较好的效果,预测与实测非常接近。曲线方程可以应用于今后的沉降观测中。其预测结果见表 1,沉降预测与实测对比曲线见图 6。

图 6 K 18+500断面沉降预测与实测对比曲线图

4 分析和结论

通过高速公路施工过程(路堤填筑、预压期、路面铺设)中的沉降观测典型数据分析,路基沉降随着加载而增长,随停载而减缓,整个沉降速率过程一直较有规律的发展。通过对沉降曲线图的观察分析可以看到,路基沉降在路基填筑初始阶段较慢,当路基填筑达到一定高度时,沉降随着填筑高度的增加迅速增大,当路基填筑即将竣工和竣工后,路基沉降又呈缓慢增加形式,直至路基完全稳定下来。利用双曲线法预测后期沉降变形,其实测数据与相对应的预测曲线吻合度较好,客观地反映了路基沉降的动态发展情况,可以科学、准确的预测路基沉降量,从而估算工程的稳定性、更好地指导施工。

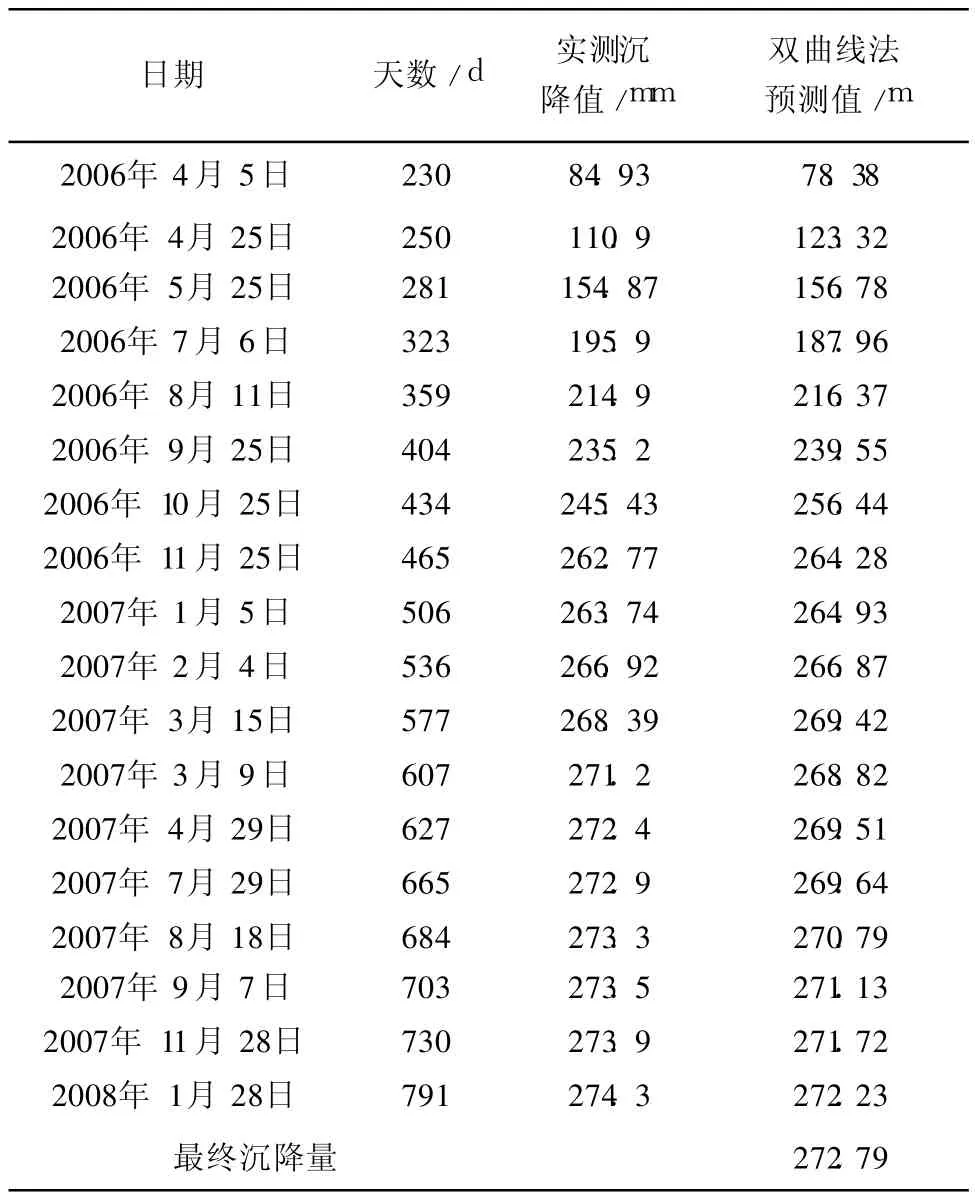
表 1 K18+500断面路基沉降预测数据表

[1] 崔希璋等.广义测量平差[M].北京:测绘出版社,1992.

[2] 赵显富.变形监测动态图形系统.武汉:武汉测绘科技大学,1996.

[3] 吴子安.工程建筑物变形观测数据处理[M].北京:测绘出版社,2002.

[4] [苏]B.H甘申等.建筑物垂直位移的观测与水准标石稳定性分析[M].北京:测绘出版社,1996.

[5] 赵显富等.高层建筑物变形监测任意点置镜交会计算[J].兰州铁道学院学报,1997,(1).