基于 IAHP 的高压配电网接线模式选取

汪铭峰， 朱铁铭， 杨京燕， 张建华

（1.华北电力大学电气与电子工程学院， 北京 102206； 2.萧山供电局， 杭州 311200）

基于 IAHP 的高压配电网接线模式选取

汪铭峰1， 朱铁铭2， 杨京燕1， 张建华1

（1.华北电力大学电气与电子工程学院， 北京 102206； 2.萧山供电局， 杭州 311200）

提出一种基于区间层次分析法的高压配电网接线模式综合决策方法， 结合实例建立 AHP层次结构，形成判断矩阵，进行一致性校验，用区间特征根法对判断矩阵的权重求解，最后求出综合权重的排序。结合实际案例介绍了该方法的计算过程，验证了该方法的可行性和有效性。

高压；配电网；接线模式；区间层次分析法；评价

高压配电网接线模式选择是电网规划和建设中的重要内容。选择与城市规划相适应的接线模式需要考虑多方面因素，如供电可靠性、经济性以及规划区域的远景目标、地理环境等。本文结合某地区实际案例，综合考虑配电网建设改造过程中影响接线模式选择的评价指标，运用区间层次分析法（Interval Analytic Hierarchy Process，IAHP）进行评价选择。区间层次分析法的应用为高压配电网接线模式选择提供了新的思路。

1 区间层次分析法（IAHP）

层次分析法 （Analytic Hierarchy Process 简称AHP）是美国著名运筹学家 T.L.Satty 提出的一种实用的多准则、 多目标复杂问题的决策分析方法[1]。它将决策者对复杂系统的决策思维过程数量化，为选出最优决策提供依据。层次分析法通过判断矩阵导出排序权值，使权值在定性的基础上得以量化， 结果更加客观。 区间层次分析法（Interval AHP 简称 IAHP）将传统 AHP 与区间数学结合，用区间数替代点值构成判断矩阵，然后通过区间数矩阵和向量计算得到各个接线模式的区间数综合权重并排序。该方法有效地描述了判断的不确定性， 增强决策结果的可信度。 基于 IAHP 的综合评判决策一般包括以下几个步骤[2]：

（1）分析系统中各因素之间的关系，建立层次结构。

（2）对同一层次的各因素与上一层次中某一准则的重要性进行两两比较，构造判断矩阵。

（3）对判断矩阵进行一致性校验。

（4）对判断矩阵权重进行求解。

（5）进行综合权重的计算和排序。

以下结合某经济开发新区高压配电网接线模式选取的实际案例介绍采用 IAHP 选取最优接线模式的详细步骤。

2 应用实例

某市的经济开发新区处于开发初期，大部分为农田和绿地，无高压配电网网架。从该新区未来的发展定位、优化电压等级以及提高经济效益各方面考虑，专家建议该新区未来的高压配电网以110 kV 电网为主， 110 kV 变电站远景年的最终规模规划为3台主变，现有图1所示的3种接线模式供选择。

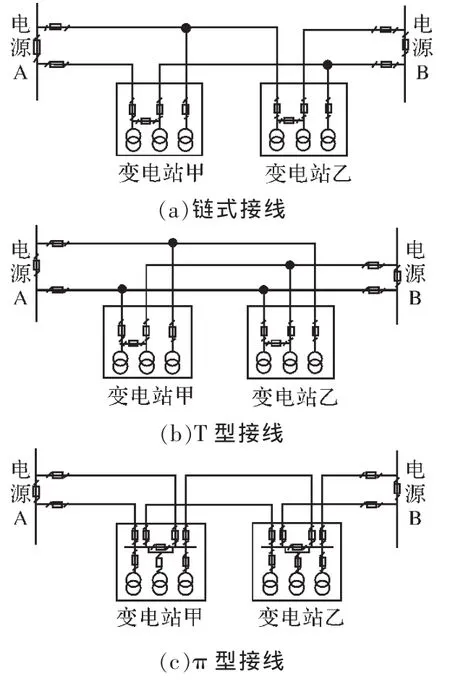
图1 3种高压配电网接线模式

图1（a）所示为链式接线模式。 该接线模式比另外两种综合投资少，但是调度的灵活性及供电可靠性不是很好。

图1（b）所示为 T 型接线模式。 该接线模式下调度维护比较方便，但是比较占线路走廊，同时供电可靠性最差。

图1（c）所示为 π 型接线模式。 在 3 种接线模式中，该模式的供电可靠性最高，但是运行方式较为多样，对调度的要求相对较高。

3 种接线模式各有优劣， 采用 IAHP 综合考虑各方面因素，最终选取最优接线模式。

方案 1： 高压配电网接线模式采用链式接线模式。

方案 2：高压配电网接线模式采用 T型接线模式。

方案 3：高压配电网接线模式采用 π 型接线模式。

3 IAHP 应用

3.1 建立层次结构

根据应用 IAHP 分析复杂问题的步骤， 确定本案的 IAHP 层次结构， 见图2。

图2 IAHP 层次结构

图2中目标层即分析问题的决策总目标：选择最佳接线模式。通过求出各方案对总目标的相对重要性评分，称为综合权重，评分最高的方案即为最优方案。准则层与子准则层包含了为实现目标所涉及的中间环节，包括技术性、经济性、社会性以及适应性四方面要求，在此之下又包含若干属性。最下端的方案层，表示为实现目标可供选择的各种措施、 决策方案， 即方案 1、 2、 3。

3.2 形成判断矩阵

在建立起层次结构后，采用两两比较的相对标量法分别构造准则层对目标层、子准则层对准则层以及方案层对子准则层的判断矩阵。

专家两两比较打分时选择互反性 1～9 标度作为区间判断矩阵的标量化方法，形成的是判断矩阵内的元素， 用区间数表示[3]。

方案层对子准则层的判断矩阵表示的是各方案对某个属性的相对优越性，称为方案判断矩阵。方案判断矩阵的构造主要基于表1所示的方案属性决策表中包含的相关数据。表中的定量数据，如“线路平均长度”、 “可靠性指标”以及“投资估算”等，可通过统计或计算得出。 而“上级电源停电影响”、 “线路走廊开辟”以及“城市协调”等因素由专家进行定性的描述，在形成方案判断矩阵时进一步量化。

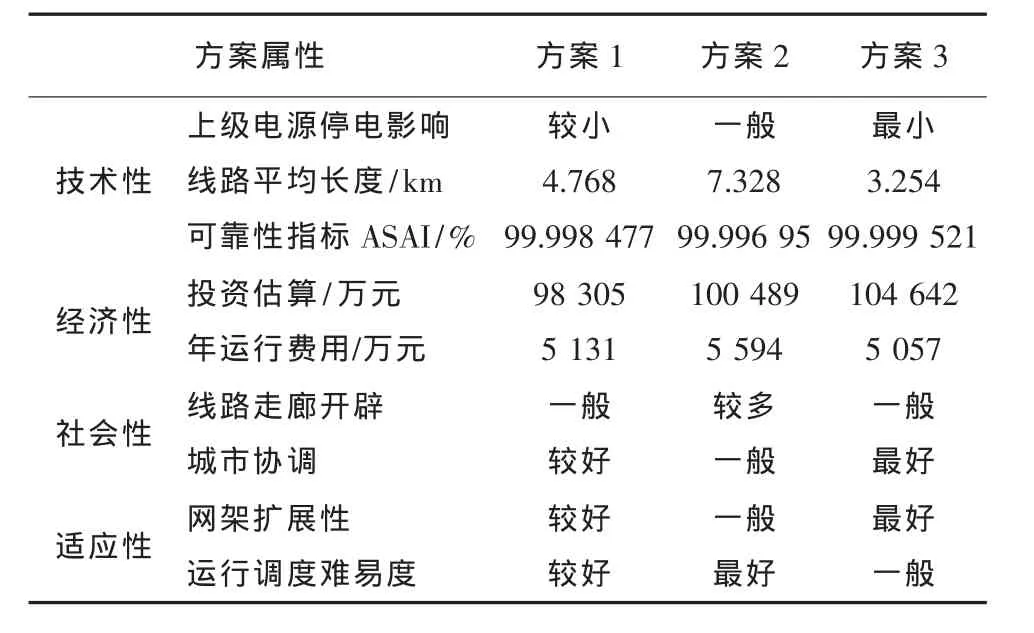
表1 方案属性决策表

3.2.1 定性数据形成判断矩阵

以表1中的上级电源停电影响属性为例介绍定性数据形成方案判断矩阵的过程。专家就上级电源停电影响属性对3个方案两两比较发现，π型接线模式时的停电影响最小，因此方案3是最好的。而T型接线模式的停电影响一般，在3个方案中属于最差，链式接线模式介于两者之间。根据评判结果得出方案1相对于方案2的优势程度介于“稍微”和“明显”之间， 量化为区间数即为[3， 4]，而方案2相对方案1的优势程度量化为区间数正好为其倒数， 即为[1/4， 1/3]。 方案 3 相对方案 1在上级电源停电影响属性上的优势程度介于 “同等”和“稍微”之间， 量化为区间数可为[1， 2]， 反过来方案1相对方案3的优势程度量化为区间数即为[1/2， 1]。 方案 3 相对方案 2 的优势程度介于“明显”和“强烈”之间， 量化为区间数即为[5， 6]，反之方案2相对方案3的优势程度量化为区间数为[1/6， 1/5]。 由此得出上级电源停电影响的方案判断矩阵如表2所示。

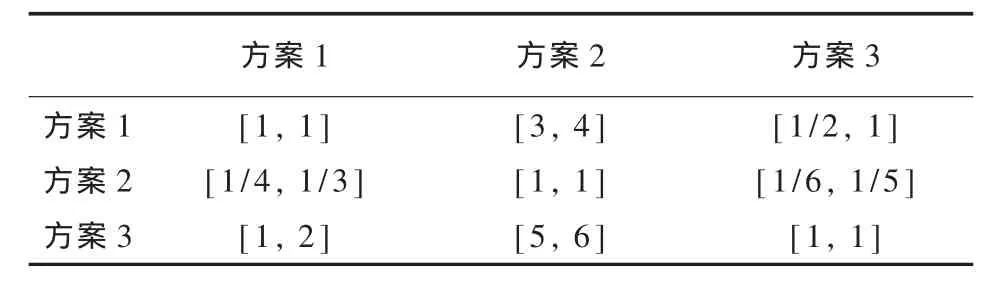
表2 上级电源停电影响的方案判断矩阵

3.2.2 定量数据形成判断矩阵

以表1中的线路平均长度这一属性为例介绍定量数据形成方案判断矩阵的过程。方案1中线路平均长度为 4.768 km， 而方案 2 中线路平均长度为 7.328 km， 专家认为线路平均长度越长越不利，规划中应尽量减小这种影响。于是用各方案的线路平均长度之比来表示方案间的相对重要性， 方案 1 相对 方案 2 的优势量化后为 7.328/ 4.768， 化为区间数即为[1.537， 1.537]。 同样可得其他方案关于这一属性的优势对比，最终得到如表3所示线路平均长度的方案判断矩阵。

表3 线路平均长度的方案判断矩阵

子准则层对准则层、准则层对目标层的判断矩阵表示的是子属性相对父属性的相对优越性，故称该判断矩阵为属性判断矩阵。属性判断矩阵的求法与方案判断矩阵的求法一致，在此不再赘述。

3.3 判断矩阵一致性校验

在专家两两比较判断的过程中，若比较量超过两个，就可能出现不一致的判断。比如就某属性的判断过程中，专家认为方案1相对于方案2的优越程度介于“明显”和“强烈”之间， 而方案 3相对于方案 2 的优越程度介于“同等”和“稍微”之间，则方案 1应该优于方案 3。 而专家在两两比较判断过程中， 可能得到方案 1 和方案 3“同等”，甚至方案1劣于方案3的结果。所以有必要对判断矩阵进行一致性校验[2]。 根据文献[4]对区间数判断矩阵一致性的定义对此进行了校验。若专家给出的信息不满足一致性，如果可能的话最好对偏好信息进行改进。

例如， 用文献[4]提供的方法判断上级电源停电影响的方案判断矩阵一致性的过程如下：

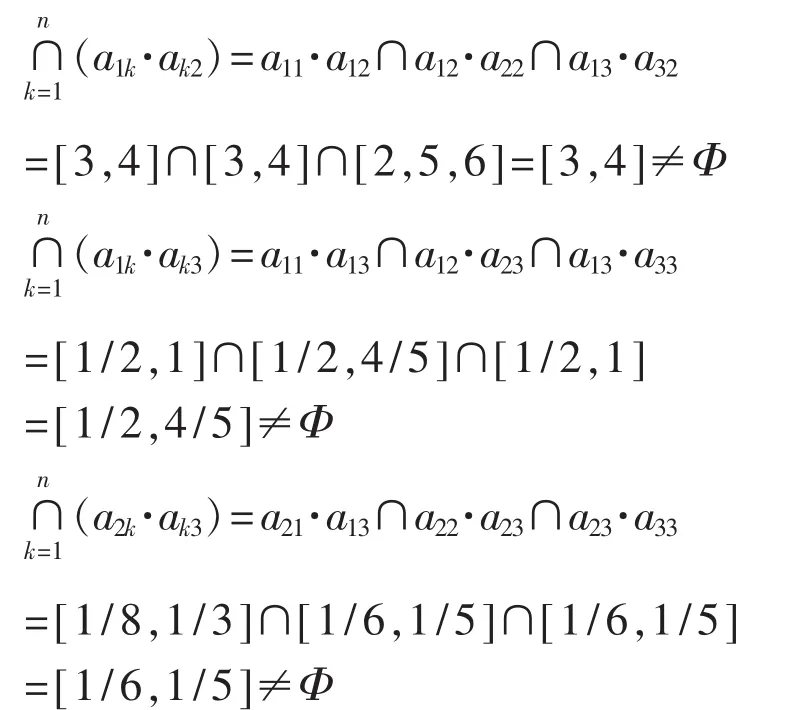
同理，可据此判断其他属性判断矩阵具有完全一致性。只有在进行完所有判断矩阵一致性校验后，才能进行判断矩阵权重的求解。

3.4 判断矩阵权重的求解

本文采用文献[5]所述的区间特征根法进行权重求解。

设 A=（aij）n×n为 区 间 矩 阵 ， 其 中记并记同样 对 区 间 向 量有

（1）求 A－， A+的最大特征值所对应的具有正分量的归一化特征向量 x－， x+。

（2）由 A－= （aij－）n×n， A+=（aij+）n×n计 算 ：

（3）得到判断矩阵权重向量 w=[kx－，mx+]。

分别得出3个方案相对于上级电源停电影响属性以及线路平均长度属性的权重如表4所示。

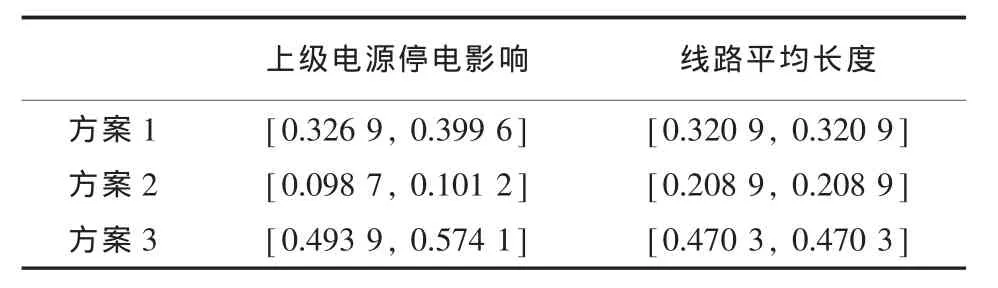
表4 判断矩阵权重求解结果

3.5 综合权重计算和排序

求得各层判断矩阵局部权重后， 采用式（1）计算方案对上一层的属性权重。

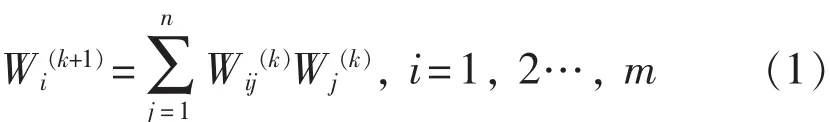
式中 ： m 为方案个数； Wi（k+1）为方 案 i对层 次 结 构中 k+1 层某属性 A（k+1）的方案权重； n 为属性 A（k+1）的 子属性个数 ；Wj（k）为 A（k+1）在 k 层 的 子 属 性 j 的权重， Wij（k）为 方 案 i对子 属性 j的方 案权重 。

依式（1）从底层开始逐层向上计算，最终可求得方案 1、 方案 2、 方案 3 的综合权重分别为[0．2952，0．3806]，[0．2389，0．2883]，[0．3437，0．4441]。

得到各方案的综合权重后，为选择最优方案还需对区间数表示的综合权重进行排序。本文采用文献[6]的排序方法对综合权重进行排序：

设 a=[a－， a+]， b=[b－， b+]是两个任意的区间数， 定义区间数 a和 b相比较时， 有 a＞b的相对优势度：

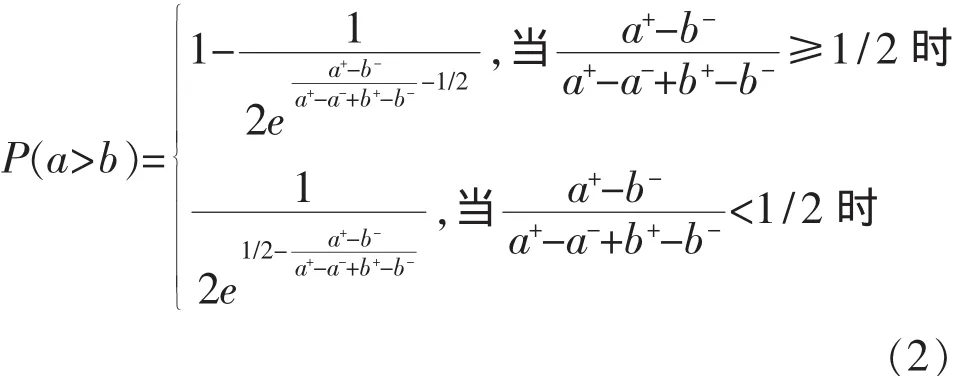
将方案 1、 方案 2、 方案 3 的综合权重按式（2）进行两两比较， 构造相对优势度判断矩阵 B 如表5所示。

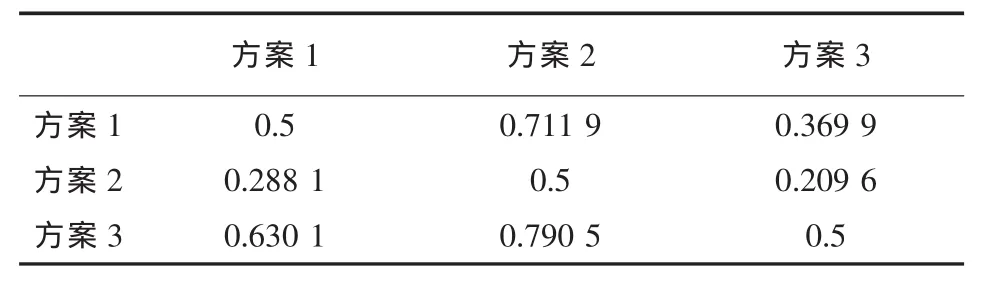
表5 综合权重排序的相对优势度判断矩阵B

最 后 根 据 相 对 优 势 度 判 断 矩 阵 B=（bij）n×n求解方案 i （i=1， 2， …， n， n 为相对优势度判断矩阵 B 的阶数， 本例中 n=3）的排序值：

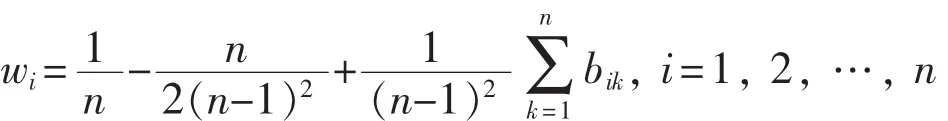
可得各方案综合权重的排序依次为 0．353 8，0．207 7， 0．438 5。 由此可得出 3 个方案从优到劣的顺序依次为方案 3， 方案 1， 方案 2。 即该经济开发新区高压配电网的接线模式宜选择π型接线模式。

4 结语

本文提出了基于区间层次分析法的高压配电网接线模式综合评判决策方法。详细介绍了综合评判 AHP层次结构的建立、区间判断矩阵形成及一致性校验、权重求解、综合权重排序的过程。该方法具可行性和实用性，可供参考。

[1]SATTY T L．The Analytic Hierarchy Process[M]．New York：McGraw－Hill，Inc，1980．[2]肖峻，王成山，周敏．基于区间层次分析法的城市电网规 划 综 合 评 判 决 策[J]．中 国 电 机 工 程 学 报 ，2004，24（4）∶50－57．

[3]吴育华，诸为，李新会，等．区间层次分析法－IAHP[J]．天津大学学报，1995，28（5）：700－705．

[4]冯向前，魏翠萍，胡钢，等．区间数判断矩阵的一致性研究[J]．控制与决策，2008，23（2）∶182－186．

[5]魏毅强，刘进生，王绪柱．不确定型 AHP 中判断矩阵的一 致 性 概 念 及 权 重[J]．系 统 工 程 理 论 与 实 践 ，1994，14（4）∶16－22．

[6]张 吉 军 ．区 间 数 的 排 序 方 法 研 究[J]．运 筹 与 管 理 ，2003，12（3）∶18－22．

（本文编辑：李文娟）

Selection of Connection M ode for H igh Voltage Distribution Networks Based IAHP

WANGMing-feng1， ZHU Tie-ming2，YANG Jing-yan1， ZHANG Jian-hua1
（1.School of Electrical and Electronic Engineering， North China Electric Power University， Beijing 102206，China； 2.Xiaoshan Electric Power Supply Bureau， Hangzhou 311200， China）

A comprehensive decision-makingmethod of selecting connection mode of high voltage distribution networks based on interval analytic hierarchy praess（IAHP） is put forward.Illustrated with an example， AHP hierachy is built to form judgementmatrix for consistence verification and the weight of IAHP judgmentmatrix is calculated by interval number eigenvalue method （IME）．At last,the ranking of each final weight is achieved．In this case,a calculation process by the method is illustrated with an example and the feasibility and effectiveness of the proposed method is verified.

high voltage； distribution networks； connectionmode； IAHP； evaluation

TM726.1

： A

： 1007-1881（2010）06-0009-04

2009-10-22

汪铭峰（1985-）， 男， 浙江江山人， 硕士研究生，主要研究方向为城市电网规划。